Уравнения Эйлера, основная формула гидростатики

Уравнения Эйлера для покоящейся жидкости и их интегрирование. Основная формула гидростатики. Закон паскаля.

Гидростатическое давление является функцией координат

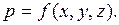
Выделим в жидкости, находящейся в равновесии, элементарный параллелепипед со сторонами dx, dy, и dz параллельными осям координат (рис. 4.1)

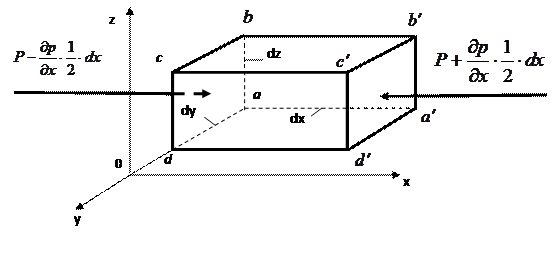
Рисунок 4.1 ‑ находящейся в равновесии, элементарный параллелепипед

Рассматриваемый параллелепипед находится в равновесии под действием:

а) массовых сил;

б) поверхностных сил давления окружающей жидкости.

Пусть p – гидростатическое давление в центре параллелепипеда. Тогда, учитывая непрерывность изменения давления в жидкости и пренебрегая величинами бесконечно малыми, стремящимися к нулю при уменьшении параллелепипеда до размеров точки, определим среднее гидростатическое давление на соответствующих гранях параллелепипеда из выражений:

для грани abcd

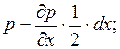
для грани

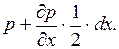
Проекции на оси x, y и z равнодействующей массовых сил, приходящихся на единицу массы жидкости (равных ускорению массовых сил), обозначим X, Y и Z.

Тогда условие равновесия сил действующих на выделенный параллелепипед в проекции на ось x запишем в виде

В виде аналогичных уравнений могут быть написаны условия равновесия в проекциях на оси y и z. После приведения подобных членов в этих уравнениях и деления на 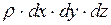, получим систему дифференциальных уравнений

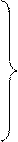
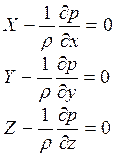, (4.1)

которая называется уравнениями гидростатики Л. Эйлера.

Умножая в системе уравнений (4.1) первое уравнение на dx, а последующие – на dy и dz и складывая их, получим

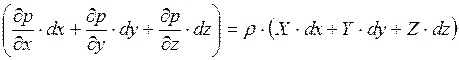. (4.2)

Составляющие левой части уравнения (4.2) представляет собой полный дифференциал. Поэтому это уравнение можно записать в виде:

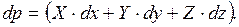(4.3)

Это уравнение называется дифференциальным уравнением равновесия жидкостей или характеристическим уравнением.

Характеристическое уравнение (4.3) позволяет определить поверхности уровня. Поверхностью уровня называются такие поверхности, в каждой точке которых данная функция координат (параметр) имеет одинаковое значение. К поверхностям уровня относятся поверхности равной температуры, равного давления, равной плотности и др. В гидромеханике наиболее часто требуется определить поверхности равного давления.

Составим уравнение поверхности равного давления. Так как в этом случае p = const, то dp = 0 и из(4.3)имеем

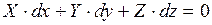, (4.4)

дифференциальное уравнение поверхности равного давления для общего случая.

Определим уравнение поверхностей равного давления, когда на жидкость из массовых сил действует только сила тяжести. При этом условии в уравнение (4.4) войдет единичная массовая сила, равная ускорению свободного падения м/с².

Направим координатную ось z вертикально вверх. Проекции ускорения g на оси координат

X=0; Y=0; Z= – g. (4.5)

Подставив данные значения в дифференциальные уравнения поверхностей уровня, получим

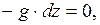
откуда имеем

z = const. (4.6)

Уравнение (4.6) описывает семейство плоскостей (горизонтальных), параллельных плоскости x O y. Следовательно, для любой горизонтальной плоскости в покоящейся жидкости, находящейся в абсолютной системе координат, давление является величиной постоянной.

Подставив в (4.3) значения проекций единичных массовых сил на оси координат из выражения (4.5), имеем

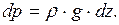(4.7)

Интегрируя уравнения (4.7), получим

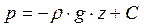
или

(4.8)

где С – произвольная постоянная интегрирования, определяемая из граничных условий (рис. 4.2). Так, при z = z_о и p = p_о получаем С = p_о + g·z_о.

Рис. 4.2

Тогда уравнение (4.8) примет вид

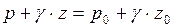
После деления (4.8) на 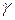имеем

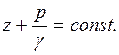(4.9)

Для любых двух точек данного объёма жидкости уравнение (4.9) можно записать в виде

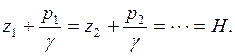(4.10)

Это уравнение выражает гидростатический закон распределения давления и называется основным уравнением гидростатики.

Постоянная величина, обозначенная H ^¢, называется гидростатическим напором.

Возьмем внутри однородной покоящейся жидкости две произвольные точки с геометрическими высотам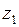и и относительно некоторой плоскости отсчёта. Давление в этих точках, соответственно, равны 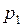и 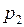и определяются уравнениями (4.10).

Увеличиваем, не нарушая равновесия в точке с 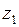, давление на 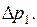В этом случае в точке с давление также должно увеличится на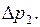

Для нового состояния основное уравнение гидростатики будет иметь вид

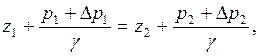(4.11)

что даёт 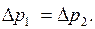Отсюда формулируют закон Паскаля: всякое изменение давления в какой-либо точке покоящейся жидкости, не нарушающее её равновесия, передаётся в остальные точки без изменений.

Дата добавления: 2015-06-26