Относительный покой среды, давление на стенки

Равновесие жидкости в цилиндрическом сосуде, равномерно вращающемся вокруг вертикальной оси. Равновесие жидкости в сосуде, движущемся прямолинейно с постоянным ускорением. Силы давления жидкости на твердые поверхности. Равномерное давление на плоскую стенку. Равномерное давление на криволинейную стенку. Неравномерное давление на плоскую стенку. Неравномерное давление на криволинейную твердую поверхность

Движение жидкости, при котором отдельные её частицы не перемещаются друг относительно друга, называется относительным покоем или относительным равновесием. Это имеет место, когда на жидкость кроме гравитационной массовой силы действуют другие массовые силы, например сила инерции.

Относительный покой жидкости рассмотрим на примере движения сосуда, наполненного жидкостью, равноускоренно или равнозамедленно в горизонтальном направлении (рис. 5.1).

Если центр О системы координат разместить в произвольной точке сосуда, то проекции единичных массовых сил будут

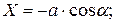
(5.1)

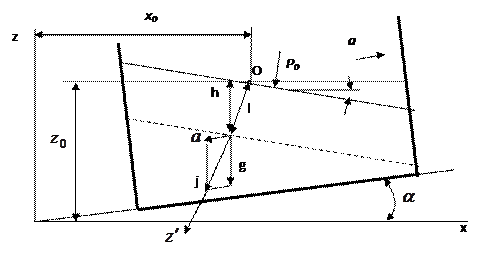Рис. 5.1

Уравнение (4.3), после замены Х, Y, Z, в соответствии с (5.1), и интегрирования примет вид

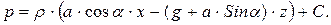(5.2)

Произвольную постоянную С определяют из граничных условий. Так, при 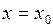и давление равно p₀ (внешнее) и произвольная постоянная

(5.3)

После подстановки выражения (5.3) в уравнение (5.2) получаем формулу для определения давления в любой точке жидкости:

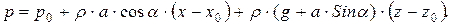
или после упрощений

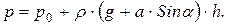(5.4)

При горизонтальном движении сосуда (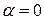) уравнение (5.3) преобразуется в основное уравнение гидростатики

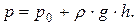
Уравнение поверхности равного давления (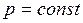) получают из зависимости (4.4), используя выражение (5.1) и граничные условия, принятые при определении давления, в виде

(5.5)

Из уравнения (5.5) получают выражение для определения угла наклона плоскостей равного давления к горизонту

Формулу для определения давления в любой точке жидкости можно получить в другом виде. Для этого, выбираем в жидкости точку М, и з которой проводим ось направленную перпендикулярно к свободной поверхности.

По оси 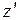направлена результирующая единичная массовая сила:

При выбранной системе координат проекции единичных сил будут

а дифференциальное уравнение (4.3) примет вид

(5.6)

После интегрирования уравнение (5.6) примет вид

. (5.7)

Произвольная постоянная С определится из условия, что при 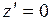давление равно 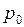, т. е.

Следовательно, давление в любой точке жидкости можно определить по формуле:

(5.8)

Из рис. 1 видно, что произведение 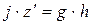и уравнение (5.8) преобразуется в основное уравнение гидростатики

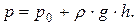
Уравнение (4.3) поверхности равного давления (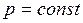) при условии и

После интегрирования этого уравнения получают

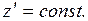(5.9)

Плоскости равного давления в жидкости, находящейся в горизонтально движущемся сосуде, представляют собой плоскости параллельные свободной поверхности жидкости.

Угол наклона свободной поверхности относительно горизонтальной плоскости

(5.10)

Гидростатическое давление представляет собой напряжение сжатия и измеряется в единицах напряжения . Если гидростатическое давление в точке равно то сила 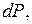действующая на элементарную площадку включающую эту точку, 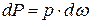и направлена по нормали к площадке

Давление жидкости на конечную площадь представляет собой равнодействующую всех элементарных сил 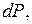действующих на элементарные площадки.

Пусть, имеем ёмкость с горизонтальным дном. Гидростатическое давление во всех точках дна будет одинаково и независимо от формы резервуара

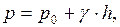
где h – глубина воды в резервуаре.

Следовательно, элементарная сила не зависит от формы резервуара

(5.11)

Полная сила давления жидкости на всю площадь дна как равнодействующая параллельных элементарных сил определится из уравнения

= (5.12)

Сила 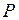состоит из двух частей: сила от атмосферного давления (), которое передаётся жидкостью по закону Паскаля, и сила избыточного давления (), зависящая от веса жидкости.

Следовательно, избыточное давление жидкости на дно ёмкости равняется весу столба жидкости с основанием, равным площади дна, и с высотой, равной глубине жидкости в резервуаре. Сила давления на горизонтальное дно одинаковой площади, одинакова независимо от формы резервуара.

Сила давления жидкости на наклонную поверхность

Определим силу 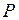давления жидкости на площадь 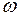, лежащую под углом к горизонту (рис. 2).

Cила давления жидкости на элементарную площадку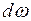

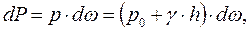(5.12)

где 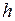– глубина погружения центра тяжести площадки .

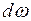Всю площадь стенки можно рассматривать состоящей из элементарных площадок 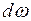, на каждую из которых действует сила давления, определяемая по аналогичной формуле и непрерывно изменяющаяся по мере изменения глубины h, но всегда направленная перпендикулярно плоскости стенки. Суммарная сила давления на всю боковую стенку будет равна сумме сил, действующих на элементарные площадки, т. е. интегралу уравнения (5.13)

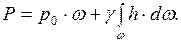(5.14)

Учитывая (рис. 5.2), что 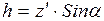, интеграл в уравнении (5.14) можно представить в виде

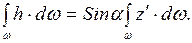(5.15)

Рис. 5.2

Интеграл является статическим моментом площади 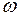и равняется произведению площади 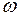на расстояние 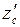от свободной поверхности до центра тяжести этой площади.

Дата добавления: 2015-06-26