Силы действующие в жидкости, нормальные и касательные напряжения, тензор напряжений

Поверхностные и массовые силы. Плотность распределения массовых сил. Закон парности касательных напряжений. Нормальные напряжения. Тензор напряжений.

Жидкости и газы всегда подвержены действию некоторых сил, которые являются в основном распределенными, т. е. приложенными во всех точках поверхности или объема. Однако в исключительных случаях в жидкостях могут действовать и сосредоточенные силы. Они возникают, например, как предельные значения распределенных сил, действующих на бесконечно малый жидкий объем, если его ускорение неограниченно возрастает.

По характеру действия распределенные силы можно разделить на поверхностные и массовые (объемные). К. первым относятся силы вязкости и давления, а ко вторым ‑ силы тяжести, инерции, электромагнитные и др.

Поверхностные силы являются результатом непосредственного воздействия на частицы жидкости соседних с ними частиц или других тел. Для качественного и количественного описания поверхностных сил служит понятие о напряжениях. В покоящемся или движущемся объеме жидкости W проведем произвольную поверхность S (рис. 8.1, а) и мысленно отбросим часть жидкости, расположенную справа от этой поверхности. Чтобы оставшаяся жидкость при этом сохранила состояние покоя или движения, приложим к ней по поверхности S распределенную систему сил, эквивалентную тому воздействию, которое оказывала отброшенную часть жидкости объемом W₂, на оставшуюся часть объемом W₁.

Рис. 8.1. Поверхностные силы и их напряжения:

а) - 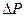- поверхностная сила, действующая на площадке ;

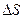б) - разложение вектора напряжения на нормальную и касательную составляющие

Пусть на элементарную площадку 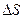, характеризуемую единичным вектором нормали n, действует сила .

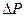Тогда

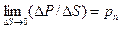(8.1)

назовем напряжением поверхностных сил в той точке, к которой стягивается площадка 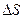. Заметим, что индекс n здесь обозначает не проекцию (ибо 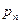‑ вектор), а ориентацию площадки 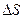в пространстве, т. е. указывает, что 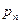‑ напряжение на площадке с нормалью n.

По отношению к площадке вектор 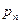в общем случае может быть направлен как угодно и потому он имеет нормальную и касательную составляющие. Из рис. 8.1, б видно, что

(8.2)

где ‑ проекция вектора 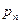на направление нормали; 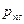‑ проекция вектора 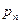на направление касательной к площадке .

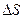В частном случае может быть 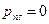и .

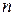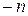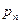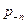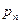
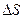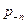
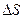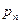
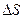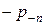
Поскольку в каждой точке поверхности S, проведенной внутри жидкости, можно указать две нормали: и (рис. 8.1, б), то им будут соответствовать два напряжения: и . Тогда силы и будут выражать взаимное действие через площадку ΔS объемов жидкости, расположенных по обе стороны от нее. Согласно третьему закону Ньютона = 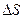или = .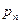

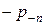Соответственно векторам 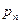и 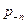будем различать две стороны площадки 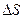, к которым эти векторы приложены, приписывая этим сторонам разные знаки.

Для характеристики массовых сил введем понятие о плотности их распределения. Если на элементарный объем жидкости действует сила 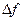, то вектор F, определяемый условием

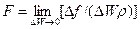, (8.3)

называется плотностью распределения массовых сил в той точке, к которой стягивается объем . Очевидно, F является массовой силой, приходящейся на единицу массы жидкости, и имеет размерность ускорения. В дальнейшем ее проекции на оси декартовых прямоугольных координат обозначаются через Fx, Fy, Fz.

Величины 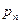и F являются основными характеристиками сил, действующих в жидкости. Они могут играть роль как внешних, так и внутренних сил. Напомним, что в механике внутренними силами системы материальных тел называют силы взаимодействия между телами, принадлежащими системе, а внешними ‑ силы воздействия на тела системы других тел, к данной системе не принадлежащих. В механике жидкой среды материальными объектами, образующими систему, являются жидкие частицы или жидкие объемы. Соответственно напряжения А и р буду внутренними, если они действуют в точках поверхности раздела между частицами или объемами, образующими выбранную систему. Если же поверхность является граничной для рассматриваемой совокупности жидких частиц системы, то напряжение 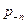- внешнее. Аналогично величина 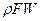может быть внутренней силой, если она создается телом, включенным в рассматриваемую систему. Так, например, сила тяжести будет внутренней для системы океан - суша и внешней для любого выделенного объема воды в океане.

Выделим в движущейся жидкости элементарный объем в виде тетраэдра, три грани которого , , 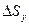, лежат в координатных плоскостях, а четвертая 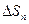нормальна направлению n (рис. 8.2). Обратим внимание на то, что грани , , 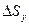, являются отрицательными площадками, поскольку нормалями к ним служат векторы - , - , - .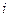

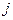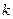Пусть 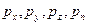‑ напряжения, действующие на соответствующих гранях тетраэдра; а ‑ вектор ускорения его центра масс. Тогда векторное уравнение движения жидкого тетраэдра, выражающее второй закон Ньютона, будет иметь вид

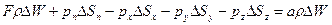
Учтем, что , и т.д.

Тогда, разделив все члены последнего уравнения на 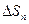, в пределе получим

(8.4)

Следовательно, напряжение на любой площадке 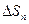можно выразить через напряжения на трех взаимно ортогональных площадках, которыми могут быть и координатные площадки. Соотношение (8.4) в проекциях на оси координат имеет вид

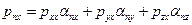
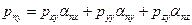(8.5)

y

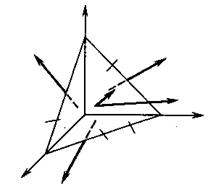
Рис. 8.2. Напряжения, действующие на гранях тетраэдра

Здесь, как можно видеть, для каждой из проекций 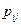употребляются два индекса, первый из которых указывает ориентацию площадки (ее нормаль), а второй – ось, некоторую тетраэдра проектируется вектор. Так, например, величина 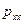, есть проекция на ось x (второй индекс) напряжения , действующего на площадке, нормальной к оси x. Поэтому 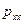, , представляют собой нормальные к соответствующим площадкам напряжения. Разноименные индексы определяют касательные напряжения. Например, есть проекция на ось z напряжения 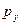, приложенного к площадке, нормальной к оси у.

В дальнейшем для краткости проекции 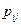напряжений будем называть просто напряжениями.

Используя уравнение моментов, можно показать, что между касательными напряжениями существует связь вида

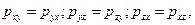
которая называется законом парности касательных напряжений.

Следовательно, напряженное состояние жидкости в точке определяется шестью независимыми скалярными величинами, три из которых являются нормальными напряжениями, а три ‑ касательными. Совокупность девяти величин типа 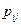, связанных соотношениями (8.5), образует тензор напряжений.

Из изложенного следует, что напряженное состояние в точке движущейся жидкости определяется тензорной величиной.

В реальных жидкостях нормальные напряжения могут создаваться как давлением одних частиц на другие, так и действием сил вязкости. Касательные напряжения являются результатом действия сил вязкости и зависят от давления лишь постольку, поскольку от него зависит коэффициент вязкости. Для модели идеальной жидкости, в которой все касательные на­пряжения равны нулю, полные напряжения направлены по нормали к соответствующим площадкам и согласно равенствам (8.5) выражаются формулами

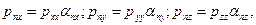(8.6)

При этом напряжения должны быть сжимающими, т. е. направленными по внутренним нормалям, так как растягивающих усилий идеальная жидкость, как и технические жидкости, не выдерживает. Поэтому величины 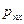, , 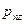можно вычислить из соотношения

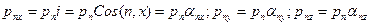(8.6')

Сопоставляя равенства (8.6) и (8.6'), получаем

Эти равенства показывают, что при отсутствии касательных напряжений нормальные напряжения не зависят от ориентации площадок и представляют собой давление р в точке жидкости, т.е.

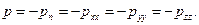(8.7)

Очевидно, в силу выражения (8.7) вектор напряжения в данном случае можно представить в виде

Знак минус показывает, что напряжение направлено по внутренней нормали, т. е. является сжимающим.

Заметим, что касательные напряжения равны нулю также в любой вязкой жидкости, находящейся в покое, так как при существовании любых сколь угодно малых сдвиговых усилий из-за легко подвижности среды произошло бы относительное перемещение слоев, т. е. жидкость была бы выведена из состояния' покоя. Следовательно, полученный вывод о независимости нормальных напряжений от ориентации площадок справедлив для любой покоящейся жидкости. Давление 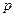в этом случае называется гидростатическим.

Дата добавления: 2015-06-26