Это число, называемое числом Рейнольдса, имеет вид

Значение числа Рейнольдса, при котором происходит переход от ламинарного течения к турбулентному, называется критическим числом Рейнольдса и обозначается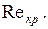

При 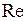> 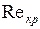– режим турбулентный, при 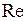< 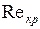– режим ламинарный.

Величина 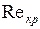зависит от условий входа, поверхности стенок, наличия начальных возмущений и т. д.

Достаточно точными измерениями движения жидкости в круглых гладких трубах, на участках достаточно удалённых от выхода и при отсутствии возмущений установлено, что при 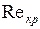_.£ 2320 режим движения будет устойчиво ламинарным.

Следует отметить, что при переходе из ламинарного в турбулентное движение 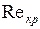имеет значительно большую величину (до 20000).

Что же характеризует число Рейнольдса? Кинетическая энергия элемента жидкости пропорциональна его объёму rV² l³ . Работа сил вязкости зависит от размера поверхности объёма m l² V. Отношение кинетической энергии элемента жидкости к работе сил вязкости

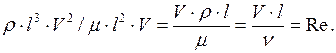
Следовательно, число 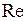характеризует относительную величину сил вязкости по отношению к силам инерции.

Определим закон, по которому распределяются скорости по поперечному сечению трубы при установившемся ламинарном режиме движения жидкости.

Как отмечалось, ламинарное движение имеет слоистый характер и происходит без перемешивания частиц. Один слой движется по другому и между ними возникает сила трения, напряжение t которой определяется законом внутреннего трения Ньютона:

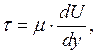
где местная скорость.

С другой стороны для слоя жидкости на расстоянии y от стенки трубы касательное напряжение определяется формулой

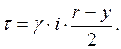
Сопоставляя эти выражения, найдём

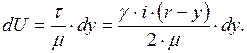
Интегрируем это уравнение:

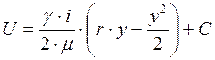
Граничным условием для нахождения 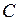является условие равенства нулю скорости на стенке, так как частицы жидкости соприкасающиеся со стенками прилипают к ним, т. е. здесь U =0 и С =0 (т. к. у =0).

Обозначим через а расстояние от оси до рассматриваемого слоя жидкости:

После подстановки получим

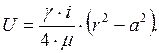
Формула известна под названием закона Стокса. Она выражает закон изменения скорости в точках поперечного сечении трубы в зависимости от расстояния точки от оси трубы. Это распределение описывается параболой второй степени (рис. 12.2).

У стенок трубы (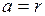) скорость равна нулю.

На оси трубы (а = 0) скорость имеет максимальное значение

Дата добавления: 2015-06-26