Интегральная форма законов сохранения. Обобщенная гипотеза Ньютона

Интегральная форма законов сохранения. Обобщенная гипотеза Ньютона о связи между напряжениями и скоростями деформаций. Установление зависимости между напряжениями в вязкой жидкости и скоростями деформаций

Уравнения (9.3) движения жидкости в напряжениях образуют незамкнутую систему. Недостающие уравнения устанавливаются на основе физических гипотез, выражающих экспериментально определенные свойства сплошных сред.

Для жидкостей и газов такой фундаментальной гипотезой служит обобщение на случай произвольного движения этих сред закона вязкого трения. Чтобы подойти к обоснованию этого обобщения, сформулируем некоторые известные данные о свойствах жидких и газовых сред:

- напряжение на произвольной площадке в общем случае можно разложить на нормальную и касательную составляющие;

- если касательные напряжения равны нулю, т. е. вектор напряжения нормален к площадке, то его величина не зависит от ориентации площадки и представляет собой давление;

- касательные напряжения порождаются только вязкостью.

Кроме того, можно показать, что вязкостные напряжения, возникающие при сдвиге одного слоя жидкости относительно другого, не только порождают касательные напряжения на произвольных площадках, но и влияют на значение нормальных напряжений.

Рис. 10.1. Схема для обоснования зависимости между напряжениями и скоростями деформаций в вязкой жидкости

Имея в виду эти замечания, допустим, что можно представить вектор 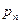напряжения в точке как сумму двух составляющих, одна из которых 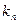обусловлена только вязкостью и не зависит от давления, а другая, зависящая от давления, нормальна к площадке и потому может быть представлена виде 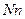, где N ‑ скаляр (рис. 10.1). Таким образом,

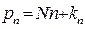(10.1)

Запишем выражение (10.1) применительно к трем взаимно ортогональным площадкам, проходящим через одну точку и расположенным в координатных плоскостях,

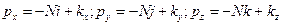
и выпишем проекции на координатные оси полных напряжений:

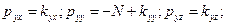(10.2)

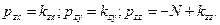
Согласно закону Ньютона вязкостные напряжения при прямолинейном движении жидкости пропорциональны скоростям угловых деформаций.

Обобщением этого факта на случай произвольного движения является гипотеза о том, что касательные напряжения, а также зависящие от ориентации площадок части нормальных напряжений пропорциональны соответствующим скоростям деформаций. Иными словами, предполагается во всех случаях движения жидкости линейная связь между вязкостными напряжениями и скоростями деформаций. При этом коэффициентом пропорциональности в формулах, выражающих эту связь, должен, быть динамический коэффициент вязкости 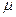, так как для прямолинейного движения эти формулы должны превращаться в формулу Ньютона для вязкостного напряжения.

Таким образом, высказанное гипотетическое утверждение можно выразить формулами:

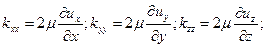
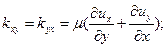
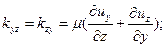(10.3)

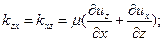
Чтобы определить введенною выше скалярную величину N, найдем среднее арифметическое из нормальных напряжений на трех площадках, расположенных в координатных плоскостях. Согласно выражениям (10.2)

откуда с учетом формул (10.3)

(10.4)

Можно показать, что в данной точке жидкости сумма имеет одно и то же значение для любых трех взаимно ортогональных площадок, проходящих через точку, т. е. не зависит от ориентации этих площадок. Иными словами, эта сумма обладает свойствами давления, а потому уместно принять гипотетическое утверждение о том, что среднее арифметическое из нормальных напряжений на трех взаимно ортогональных площадках, проходящих через одну точку, есть взятое с обратным знаком гидродинамическое давление в этой точке, т. е.

(10.5)

и, следовательно,

.

Зависимость (10.5) нельзя строго доказать, она представляет собой гипотезу, которую можно считать косвенно подтвержденной всей практикой современной гидромеханики, поскольку пока нет фактов, опровергающих эту гипотезу. Теперь окончательные выражения для нормальных и касательных напряжений в вязкой жидкости можно записать в виде

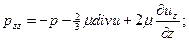(10.6)

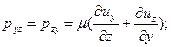
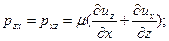
Для несжимаемой жидкости 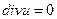, и выражения для нормальных напряжений упрощаются:

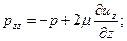(10.7)

Таким образом, соотношениями (10.6) устанавливаются зависимости между напряжениями в вязкой жидкости и скоростями деформаций. Они позволяют исключить из уравнений движения (9.3) все компоненты тензора напряжений, заменив их давлением p и скоростями деформаций.

Дата добавления: 2015-06-26