Уравнения движения в напряжениях

Вывод уравнений движения жидкости в напряжениях. Интегральная форма уравнения движения жидкости. Векторная форма уравнения движения жидкости в напряжениях.

Для вывода уравнений движения жидкости выдели; произвольный жидкий объем W, ограниченный поверхностью S, и запишем для него уравнение, выражающее закон количества движения: производная по времени количества движения системы равна сумме действующих на нее внешних сил.

Поскольку на каждую единицу массы действует сила F, главный вектор массовых сил выражается интегралом .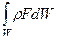

Главный вектор поверхностных сил получим, суммируя элементарные силы 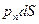, распределенные по поверхности S: .

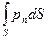Количество движения 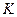массы жидкости в объеме W и его производную выразим интегралами

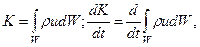
где u ‑ скорость движения центра масс объема .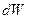

Уравнение количества движения запишем в форме

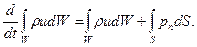
Левую часть его представим в виде

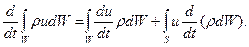
Полагая массу жидкого объема постоянной, заключаем, что 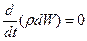. Тогда уравнение количества движения примет вид

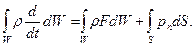(9.1)

Это уравнение представляет собой интегральную форму уравнения движения жидкости. Чтобы получить его дифференциальную форму, преобразуем поверхностный интеграл, входящий в него, в объемный. Для этого учтем, что согласно выражению (8.4)

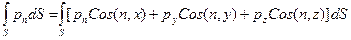
Используя известные из векторного анализа формулы, справедливые для любого вектора G,

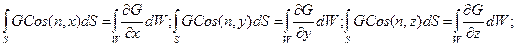
Получим

Подставив это выражение в уравнение (9.1) и записав все члены уравнения по одну сторону от знака равенства, находим

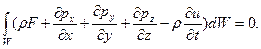
Поскольку это уравнение должно быть справедливым для любого объема W, то из равенства нулю интеграла вытекает равенство нулю подынтегральной функции.

Таким образом,

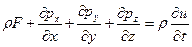(9.2)

Выражение (9.2) представляет собой векторную форму искомого уравнения движения жидкости в напряжениях, который эквивалентно трем уравнениям в проекциях, имеющим вид

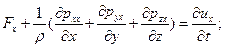
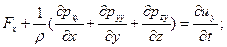
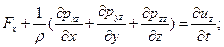
В систему уравнений (9.3), называемых уравнениями движения в напряжениях, входят в качестве неизвестных функций три проекции скорости 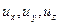и шесть независимых компонентов тензора напряжений: 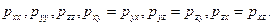Проекции массовых сил 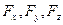как правило заранее известны. Поэтому для несжимаемой жидкости система (9.3) включает девять неизвестных функций и, следовательно, является незамкнутой. Для сжимаемой жидкости (газа) в числе неизвестных должна быть включена также плотность 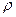; поэтому, хотя систему (9.3) можно дополнить уравнением неразрывности, содержащим плотность и проекции скорости, этого оказываете недостаточно для того, чтобы она была замкнутой. Необходимо ввести в рассмотрение еще какие-нибудь связи между указанными функциями. Такие связи можно установить только путем принятия некоторых гипотез, основанных на данных наблюдений, выражающих физические свойства жидкостей. Наиболее просто система (9.3) замыкается для случая покоящейся жидкости. Обратим внимание на физическое содержание уравнений (9.1) и (9.2). Они выведены из закона количества движения системы, которая для случая сплошной среды образуется непрерывно совокупностью жидких частиц, составляющих объем W. Поэтому указанные уравнения можно рассматривать как специфические для жидкой среды формы уравнения количества движения. Но при сделанном предположении о постоянстве массы жидкого объема эти же уравнения можно вывести непосредственно из второго закона Ньютона или принципа Даламбера. Поэтому уравнении (9.1) и (9.2) можно также рассматривать как соответственно интегральную и дифференциальную формы второго закона Ньютона для жидкого объема. При этом левая часть уравнения (9.1) представляет собой суммарную инерционную силу, а правая ‑ сумму действующих на массу жидкости внешних сил. В уравнении (9.2) правая часть выражает произведение массы на ускорение (силу инерции) для единичного объема, а левая сумму действующих на него массовых и поверхностных сил.

Дата добавления: 2015-06-26