Учитывая, что , получаем

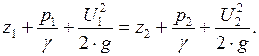
Это и есть уравнение Бернулли для элементарной струйки. Его можно представить в разностной форме

или, обозначая разности между величинами в виде приращений,

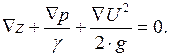
При неограниченном сближении сечени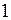й и 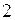уравнение можно представить в дифференцированной форме

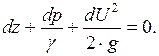
Так как сечения 1 и 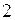взяты произвольно, то уравнение Бернулли можно также записать в виде

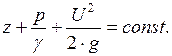
Рассмотрим вначале геометрическое истолкование. Отнеся струйку к горизонтальной плоскости , напишем уравнение Бернулли для двух сечений этой струйки

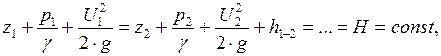
где 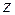– геометрическая высота центра тяжести сечения над плоскостью 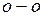; 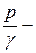пьезометрическая высота; 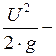скоростная высота.

Для каждого сечения элементарной струйки величина H может быть представлена совокупностью отрезков 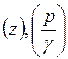и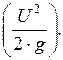

Соединив между собой концы отрезков H, получим кривую или плоскость, называемые плоскостью или линией полного напора.

Соединив кривой концы отрезков 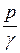, получим линию, называемую пьезометрической линией.

Итак, рис. 13.2 даёт геометрическое изображение уравнения Бернулли. Можно видеть, как по длине струйки меняются слагаемые уравнения. Если сечение расширяется, то уменьшается скоростной напор, но возрастает
сумма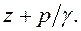

Если рассматривать уравнение Бернулли как уравнение энергии, то каждое слагаемое этого уравнения следует рассматривать как составляющую полной энергии (потенциальную или кинетическую) и каждое из этих слагаемых должно измеряться в единицах работы. Составляющие уравнения имеют линейную размерность, и, чтобы перевести это уравнение в уравнение работы, надо умножить его на единицу силы. При умножении его на 1 Н уравнение не изменится, но размерность будет выражена в 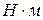и будет представлять собой энергию единицы веса жидкости, проходящей через данное сечение. Такую энергию называют удельной. В соответствии с этим: 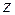– удельная энергия положения (потенциальная); 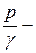удельная потенциальная энергия давления; 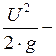удельная кинетическая энергия.

Легко видеть, что с энергетической точки зрения уравнение Бернулли показывает, что сумма потенциальной энергии (положения и давления) и кинетической энергии есть величина постоянная.

Таким образом, уравнение Бернулли представляет собой физический закон сохранения механической энергии при движении идеальной жидкости.

Дата добавления: 2015-06-26