Народонаселение 2 страница

негры, индейцы и переселенцы разных стран, и этих последних, очевидно, нельзя ставить в один разряд с жителями, родившимися в самих Штатах. В этом отношении американские переписи дают всю возможность сделать различение, и приводимые ниже числа относятся лишь к белым жителям штатов, родившимся в них от матерей и отцов — уроженцев самих Штатов.

Приводимые далее числа взяты не из последней переписи Штатов (1900), а из предшествующей, 11-й переписи 1890 г., так как томы последней переписи дошли до меня лишь недавно. По 11-й переписи, всех жителей в 1890 г. было 62,6 миллиона, но в их числе природных белых жителей от матерей и отцов, в Штатах родившихся, было только 34,3 миллиона, и вот они-то сочтены в нашем дальнейшем расчете (исключая лишь 47 тыс. жителей неизвестного возраста). В прилагаемой табл. 1 для

Таблица 1

Возраст, лет, от—до	Германия, 1890—XII, тысяч жителей	Родившихся белых в С.-А.С.Штатах, тысяч жителей	В процентах. Число жителей:
Германия	С.-А.С. Штаты	среднее
0—5	6 429	4 551	13,01	13,28	13,14
5—10	5 531	4 432	11,19	12,93	12,06
10—15	5 412	3 965	10,95	11,57	11,26
15—20	4 803	3 553	9,72	10,37	10,04
20—25	4 257	3 185	8,61	9,29	8,95
25—30	3 745	2 545	7,58	7,43	7,50
30—35	3 387	2 377	6,85	6,93	6,86
35—40	2 920	2 054	5,91	5,99	5,95
40—45	2 689	1 719	5,44	5,02	5,23
45—50	2 442	1 471	4,94	4,29	4,62
50—55	2 139		4,33	3,66	4,00
55—60	1 729		3,50	2,73	3,11
60—65	1 423		2,88	2,32	2,60
65—70	1 145		2,32	1,69	2,01
70—75			1,56	1,22	1,39
75—80			0,80	0,71	0,75
80—85			0,31	0,38	0,34
85—90			0,09	0,14	0,12
90— N			0,02	0,05	0,04
Итого:	49 428	34 270

Германии и Штатов приведены не только абсолютные числа в тысячах жителей каждого возраста, но и про-

центные количества лиц каждого возраста, чтобы дать легкую возможность сделать сличение. Ввиду сходства процентных чисел в последнем столбце дан средний процент возрастного состава.

Исходом в первом столбце служит возраст, считая 5 лет за единицу, и если стоит, например, число 30—35, то это значит, что табличное число показывает число жителей в возрасте более 30 лет, но менее 35 лет. Приводить же числа по годам, например от 1 года до 2 лет или от 30 до 31 года, было бы не только неудобно по множеству чисел, но и непоучительно, потому что какой-нибудь правильности можно ждать только от средних больших величин, а в мелочах и частностях можно подразумевать всегда мелкие неправильности, зависящие от множества обстоятельств, например от недородов в известные годы, от войн, от присоединения новых областей и т. п., что падает на определенные времена, отвечающие рождению лиц данного возраста. Такие частные влияния до некоторой степени сглаживаются, когда в таблицах приведено количество людей в возрасте, различающемся на 5 лет, как это сделано в прилагаемой таблице. Притом не подлежит сомнению, что точность показания возраста при переписях сравнительно невелика, так как точная проверка о возрасте каждого жителя совершенно невозможна. Если же взять пятилетний промежуток, то, деля число жителей каждого возрастного периода на 5, мы получим число жителей в среднем возрасте, например из числа жителей 30—35 получим, деля на 5, число жителей в возрасте от 32 до 33 лет, что и обозначено далее чрез 33. При этом делается, конечно, предположение, что в течение 5 лет возрастание идет арифметически пропорционально годам, т. е. выражается линейным образом по годам. В частности, т. е. в узком пределе лет, это всегда можно допустить, принимая во внимание возможные погрешности каждого отдельного числа, отнесенного к году. Выражаясь алгебраически, всякую небольшую долю кривой линии можно представить в виде прямой линии. Но это, конечно, не относится ко всей совокупности чисел, потому что они выражаются не прямою, а кривою линиею, которая одна и представляет свой особый интерес, выражая собой изменчивые отношения между числом лет n и числом жителей данного возраста, которое мы означаем через у. Отношения

этих чисел мы далее рассмотрим, приведя исходную таблицу. Оригинальные числа для Германии взяты из «Statistisches Jahrbuch fur das Deutsche Reich fur 1900», стр. 3, а для Штатов — из «Abstract of the eleventh census 1890», стр. 58.

Из приведенной 1-й таблицы видно, что относительное (процентное) число жителей разного возраста в Германии и Штатах чрезвычайно близко, отчего и можно было взять среднее и в этом среднем у, отнесенном к определенному году n, можно ждать уже сглаживания частных погрешностей отдельных переписей, потому что среднее относится к 85 млн.жителей. Этого же среднего, до некоторой степени сглаженного результата можно достичь еще лучше, складывая первоначально абсолютные числа для Германии и Штатов и выводя из этой суммы указанный результат по годам n через 5 лет. Так и сделано во второй таблице, в столбце, обозначенном чрез у,

Таблица 2

Возраст лет от—до	В 1890 г. жителей Германии и С.-А. С. Штатов. Тысяч или процентов	В возрасте от п — 1 до п лет процентов жителей у, по переписи 1890 г.	По формуле величина у, считая
N=105;	N = 110 г.
0—5	10 980	Или	13,12%	n = 3 у = 2,62	2,74	2,62
5—10	9 963	»	11,90%	n= 8 у = 2,38	2,47	2,38
10—15	9 377	»	11,20%	n = 13 у = 2,24	2,23	2,15
15—20	8 356	»	9,98%	n= 18 у = 1,99	1,99	1,93
20—25	7 412	»	8,89%	n = 23 у = 1,78	1,77	1,73
25—30	6 290	»	7,52%	n = 28 у = 1,50	1,56	1,54
30—35	5 764	»	6,88%	n = 33 у = 1,37	1,36	1,36
35—40	4 974	»	5,94%	n = 38 у= 1,19	1,18	1,18
40—45	4 408	»	5,27%	n = 43 у = 1,05	1,01	1,03
45—50	3 914	»	4,68%	n = 48 у = 0,93	0,85	0,88
50—55	3 395	»	4,06%	n = 53 у = 0,81	0,71	0,77
55—60	2 664	»	3,18%	n = 58 у = 0,63	0,58	0,62
60—65		»	2,65%	n = 63 у = 0,53	0,46	0,51
65—70	1 724	»	2,06%	n = 68 у = 0,41	0,36	0,40
70—75	1 190	»	1,92%	n = 73 у = 0,28	0,27	0,31
75—80		»	0,77%	n = 78 у = 0,15	0,19	0,23
80—85		»	0,34%	n = 83 у = 0,07	0,13	0,16
85—90		»	0,11%	n = 88 у = 0,02	0,08	0,11
Выше 90		»	0,03%	n=(N-90)/5 0,01	0,05	0,10
	83 699 тыс.		100%	Сумма разностей	+D = +0,44 +0,36
—D = —0,47 —0,43
М = 26,6 27,9

выражая опять число жителей в процентах. Числа этого столбца, конечно, очень близки к числам последнего столбца предшествующей таблицы. Но в них все же должно ждать ряд разных мелких погрешностей, неизбежно свойственных как самим, так и рассчитанным из них результатам.

Полученные таким образом числа для у приведены в табл. 2 в столбце со знаком у. Сличение этих чисел с ранее выведенными показывает, что разность между ними очень невелика и касается только десятых долей процента, что допустимо уже по необходимости ждать в переписях лишь относительной точности, так как абсолютная точность ни в этих, ни в каких опытных числах по самому существу невозможна.

Желая узнать сущность закона распределения жителей по возрастам, остановимся над соотношением полученных у и n. Для них необходимо ждать еще некоторых отступлений, зависящих в данном случае, например, от того, что в 60-х годах в Америке господствовала междоусобица между северными и южными штатами, а в то же время Германия вела войну с Австрией и к началу 70-х годов вела большую войну с Францией, что должно было нарушать не только стройность чисел рождаемости, но и смертность для лиц в зрелом военном возрасте, а это должно отразиться на числе жителей, родившихся в этих и следующих годах (т. е. для лиц, имеющих при переписи 30—40 лет), и на числе мужчин в возрасте около 50— 60 лет, потому что они были во время этих войн в цветущей молодости, преимущественно падавшей во время войн. Не умножая подобных примеров, должно ясно сознавать, что наблюдение и расчет должны между собой немного отличаться, если отыскивается закон нормального распределения по возрастам, который один представляет свой научный интерес. Но и указанные отступления от нормы не должны по существу превосходить некоторого, притом небольшого, предела; например, не должны касаться целых процентов, а ограничиваться их долями, потому что числа извлечены из целого числа миллионов, а отступления касаются только сотен тысяч. Сколько мне известно, еще никто не принимался за вопрос о нормальном законе распределения числа жителей по возрастам, и если я решаюсь приняться за такой трудный новый вопрос, то лишь по той причине, что верю

в закон больших средних чисел и в правильность всяких отношений, кажущихся на первый взгляд зависящими лишь от частной воли и от случайного сцепления обстоятельств. Эта уверенность внушена долгим изучением явлений природы, а оно приводит к заключению, что все крупное общее среднее всегда оказывается закономерным, хотя всегда состоит из ряда мелочей, носящих на первый взгляд капризный индивидуальный характер. Максвелевская теория газов — лучший пример для этого, и я не упущу случая внушить молодежи склонность к изучению представлений, подобных максвелевским, если хотят разобраться в вопросах социологии. Не желая усложнять изложения, я ограничиваюсь этим намеком и обращаюсь к примеру распределения народонаселения по возрастам как к такому, в котором можно уже видеть значение общих крупных чисел и закономерную в них стройность. Ведь механику, физику, химию изучали сперва исключительно приемами качественными и описательными, причем были в сущности рабами действительной природы, а понемногу становятся ее господами, подмечая присущую явлениям этого рода закономерность. Ведь и там изучению подлежат лишь частности, и всякое измерение сопряжено с неизбежными погрешностями, а общее крупное оказывается состоящим из данного числа мельчайших капризных отдельностей, в крупном же общем среднем все эти мелкие капризы исчезают, и тогда выступает основной, Божеский закон, который один делает рабов действительными господами предпринимаемого и предстоящего. Не только в переносном, но и в подлинном смысле отдельный человек есть не что иное, как атом, и в совокупности людей, т. е. в крупных числах, до них относящихся, должно ждать такой же простоты и правильности, как в числах, получаемых от так называемой мертвой природы. Вот одна из тех заветных моих мыслей, которую очень желательно мне внушить будущим поколениям русского юношества, приложение которой к действительности я желал бы демонстрировать при помощи данных о народонаселении, и прежде всего о распределении по возрастам. Беглый взгляд на графическое выражение зависимости между у и n показывает уже, что они расположены по стройной, или, как привыкли выражаться математически, правильной, кривой линии. Найти законность — значит найти алгеб-

раическую зависимость между у и n, т. е. между возрастом и числом жителей этого возраста. Геометрические соображения простейшего свойства показывают, что первое приближение к истине получится уже тогда, когда эту зависимость представим в виде вертикальной параболы, т. е. выразим

у = А + Вn + Сn² (I)

где А, В и С — суть постоянные числа, а у и n — переменные (ординаты и абсциссы кривой). Ни одной минуты я не думаю, что такое выражение есть окончательное и вполне точное, утверждаю только, что оно очень близко удовлетворяет действительности и отступает от нее лишь на величины недалекие, подобные разностям между у 1-й и 2-й таблиц. Числа, разочтенные по формуле, приведены в последних столбцах табл. 2. Сходство вычисленных и наблюденных у наглядно показывает степень применимости вышеозначенной формулы. Для ее нахождения, т. е. для определения численных значений коэффициентов А, В, С, очевидно, достаточно трех данных, а их гораздо более. Каждые три данные у и n дадут свои коэффициенты, нужно найти некоторые вероятнейшие А, В и С и можно было бы руководствоваться при этом правилами способа наименьших квадратов, а так как n равно отстоят друг от друга, то можно было бы прибегнуть к известному приему моего покойного друга П. Л. Чебышева, развитому мною при исследовании колебания весов. Но в данном случае есть два соображения, упрощающих дело. Во-первых, n есть число не беспредельно большое, а ограниченное некоторым пределом N, показывающим тот средний наибольший возраст, примерно около 100 лет, до которого доживают люди в настоящее время и при котором их число впадает в пределы точности опытных чисел и выводимой формулы ⁸.

⁸ Я убежден, что этот предельный возраст N с народами и веками изменяется, и даже имею повод полагать, что он впоследствии и с развитием образованности будет возрастать отчасти, как стараюсь показать в дальнейшем изложении, т. е. полагаю мафусаиловы года не как единичное исключение, а как норму ожидать должно впереди, а не оплакивать где-то сзади. Франция до некоторой степени уже начала оправдывать такое ожидание, потому что в ней стариков в возрасте 80 лет и выше гораздо больший процент, чем у народов более молодых. По этой причине мне особо симпатичны попытки моего друга профес-

Следовательно, при n= N величина у может быть принята равной нулю. В то же время должно признать прямо, судя по числам и действительности, что у, или число жителей, достигает при возрасте N своей наименьшей величины, а потому на основании известного закона минимумов В + 2Сn при этом равно 0, т. е. В = — 2CN. Во-вторых, выражая у в процентах, очевидно, что сумма всех у от 0 до N = 100, что разрешает отношение между С и N и приводит к следующему выводу, касающемуся А, В и С в формуле (I), а именно ⁹:

А = CN²,

В = — 2CN,

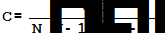
Подставляя эти выражения для А, В и С в уравнение (I), получим

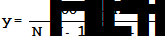(II)

сора Мечникова разыскивать физическую причину старчества и средства бороться с этими причинами. Далее, я полагаю, что с увеличением процента бодрых стариков человечество должно будет улучшаться, потому что такие старики, умудренные опытом жизни, благотворно будут влиять на молодежь, каким бы самомнением она ни заразилась. А так как я жду увеличения процента стариков в будущем, с умножением общего числа людей и всей цивилизации, то в этом нахожу своего рода успокоение, в сущности основанное на том, что впереди человечеству будет лучше житься, чем жилось до сих пор. Сухая формула распределения народонаселения по возрастам и указание на то, что есть уже начало возрастания числа стариков у народов наиболее образованных, убеждают меня в осуществимости такого «профессорского мечтания».

⁹ Для лиц, интересующихся способом вывода этих равенств, сошлюсь на то, что они даны мною первоначально в моем сочинении «Учение о промышленности» (2-й выпуск, стр. 159), и затем привожу изложение вывода, сделанное моим сыном, И. Д. Менделеевым.

По смыслу вопроса коэффициенты уравнения

y = А + Вn + Сn² (I)

должны быть найдены так, чтобы удовлетворились следующие условия: 1) наименьшее значение у в уравнении (I) должно быть при n =N (заданном числе); 2) это значение у должно быть равно нулю; 3) сумма

Это показывает, что по первому приближению, или первой законности в распределении числа жителей по возрастам, значение у-ов исчерпывается знанием n-ов и одним постоянным предельным возрастом N, а через это нахождение всей зависимости между у и n упрощается до крайности, т. е. из каждого отдельного значения и соответствующего ему n получается свое N. Если N расчесть на основании данных для малых возрастов,

всех значений у в уравнении (I) при изменении n от 1 до N (в целых числах) должна равняться 100.

Эти условия позволяют вычислить коэффициенты уравнения (I) в зависимости от N следующим образом.

При наименьшем значении у' а производная от А + Вn + Сn² должна равняться нулю, т.е. 2Сn + В = 0, откуда

B = —2Cn

или по условию 1)

В = — 2CN. (II)

Но по условию 2)

А + (— 2СN) N + CN² = 0, откуда A = CN². (III)

Подставляя найденные значения А и В в уравнение (I), получим

у = CN² — 2CNn + Сn²

или

y = C(N-n)² (IV)

Для выражения С чрез N служит условие (3), которое выражается так:

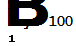
или по уравнению (IV)

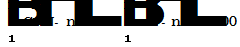
откуда

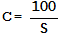
но

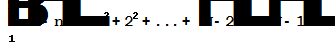
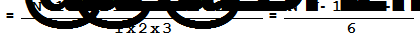(V)

Подставляя значение С в выражения (II) и (Ш), находим выражения для А и В в зависимости от N, а подставляя в уравнение (IV), находим зависимости у от N:

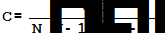
то выходит N не менее 110, даже до 115 лет. Если же это сделать на основании чисел уже стариков, то N выходит не только гораздо меньшим, но даже меньшим 100 лет, показывая этим, что в последние десятилетия вместе с возрастанием прироста (с отсутствием войн, развитием просвещения и пр.) увеличились условия для продолжительности человеческой жизни. Это определяется, по всей вероятности, не столько успехом медицины и гигиены, сколько развитием благосостояния и уменьшением шансов погибнуть в зрелом возрасте, не доживая до старости; получаемые для разных значений л величины предельного возраста N, очевидно, не могут быть тождественны между собою и, тем ближе к истине или вероятнейшему, чем более величина у. На основании этого и рассчитана средняя величина N, и она оказалась лежащею вблизи от N =105 до N = 110 лет для той совокупности данных, которые взяты из приведенных выше переписей Германии и Соединенных Штатов. Подставляя эти числа, получаем

у = 0,000 2629 (105 — n)²

у = 0,000 2285 (110 —n) ². (Ш)

Числа, рассчитанные по этим выражениям, приведены в последних столбцах табл. 2. Необходимость привести два ряда разочтенных чисел отчасти еще выясняется из последующего изложения.

Сличение разочтенных чисел с наблюдением для у-ов показывает, что наши выражения (I) или (II) вообще, а в частности (III) для Германии и Штатов недалеко отступают от действительности, т. е. что распределение населения по возрастам довольно точно выражается параболою 2-го порядка, т. е. в таком деле, как распределение по возрастам, господствует в норме при данных условиях правильная общая закономерность, что и требовалось показать для того, чтобы понемногу вселять убеждения в правильной закономерности социальных отношений, кажущихся капризными и сбивчивыми. Для показания этого же общего начала я приведу еще одно доказательство, относящееся к общему числу жителей С.-А. С. Штатов, но предварительно считаю не лишним остановиться над некоторыми обстоятельствами, относящимися к возрастному распределению. Напомню, однако,

вновь о том, что я не считаю свою формулу окончательною, а потому делаю лишь намеки на то, чего можно достичь со временем, когда найдется истинная формула и когда можно будет выводить из нее совершенно строгие следствия. Те следствия, которые выводятся из принятой нами формулы, очевидно суть только приблизительные, но и они наводят на такие размышления, которые, кажется, не следует упускать социологам из вида. Притом следствий этих много, а я могу здесь остановиться лишь над немногими из них, касающимися рождаемости, смертности, средней продолжительности жизни и среднего возраста всех жителей разных стран. Надо повторить при этом, что, признавая выставляемую закономерность лишь дающею первое приближение к истине, нельзя ручаться за полную точность выводимых следствий, но тем не менее над ними следует остановиться для того, собственно, что очень часто, особенно за последний век, числами, так сказать, баловались, не заботясь о приложении полученных выводов к каким бы то ни было жизненным явлениям, а моей заветною мыслью служит то соображение, что математический разбор явлений действительности тогда только служит для надлежащего уяснения предмета и для истинного познания вещей, когда он не только выводится из действительных данных, но когда в то же время он и дает следствия, непосредственно с действительностью связанные и представляющие для нее свой интерес.

Рождаемость, выраженная в процентных числах жителей, весьма сильно изменяется по странам, т. е. гораздо значительнее, чем распределение по возрастам. Для России она близка к 4,8%, а во Франции — к 2,5%; для других же стран Европы получаются промежуточные числа. Из формул можно полагать или ждать, что при N = 105 рождаемость (n = 0) выражается¹⁰ 2,77%, а при N = 110 она рассчитывается равною 2,76%. Для Германии рождаемость достигает ныне 3,7%, если считать и мерт-

¹⁰ Если бы числа у выражали непрерывное изменение числа жителей при соответственном непрерывном же изменении возраста n, то число родившихся в единицу времени должно было бы выражаться величиною у при n = 0, но при переписях дается число жителей для возраста от n — 1 до n лет и значение n, очевидно, прерывное, начинающееся лишь от n = 1, отвечающее затем 2, 3 до N целых лет, а потому n не может иметь нулевого значения, а потому расчет рождаемости

ворожденных, а за их исключением все же более 2,7— 2,8%, а именно около 3,5%. Мне кажется, однако, что причину разности расчета от действительности должно приписывать не столько неполной точности нашей формулы, сколько тому, что в первое время после рождения и в Германии, как повсюду, мало умеют ухаживать за детьми и часть рожденных можно как бы причислить к мертворожденным, т. е. не считать в общем счете жителей. Но так как я считаю свою формулу (I) и (II) лишь первым приближением и рождаемость представляет своего рода экстраполирование (т. е. расчет за пределом исходных данных, которые у нас начинаются с n = 1), то и не считаю надобным более останавливаться над этим предметом особенно потому, что в некоторых странах (Бельгия, Швейцария, Ирландия) распределение по возрастам близко отвечает нашему расчету (по III формуле) и в них рождаемость близка к 2,7%, т. е. к формульной. Мне кажется даже, что совпадение для некоторых стран (Бельгия, Швеция и др.) рождаемости с выводом, получаемым из распределения по возрастам, показывает, что в этих странах умеют столь же хорошо ухаживать за беременными матерями и новорожденными, как за лицами других возрастов. В других же странах, например у нас в России, большой процент смертности в первые месяцы жизни не только не отвечает распределению жителей по возрастам, но и заставляет ждать преувеличенного числа или коэффициента рождаемости, показывая недостаточное знакомство жителей с гигиеной младенцев, бедность родителей, т. е. скудость страны и недостаток в ней медицинской помощи. Затем не излишне указать на то, что с увеличением предельного возраста N процент рождаемости должен падать. Объяснение этому видно уже из того, что с увеличением предельного возраста должно возрастать число стариков и старух, не способных к деторождению, и уже чрез это одно процент рождаемости должен падать.

по числам переписей содержит в себе произвольную, новую гипотезу. Но ее справедливость в некоторой мере фактически подтверждается тем, что из чисел, разочтенных в нашей таблице, выходит, что при n = 0 (когда у = А = CN²) получается у = 2,76, что близко к проценту рождаемости в Германии, так как он в ней (ук. соч., стр. 13) в период 1871—1880 гг. равнялся 2,88%, а в следующее десятилетие — 2,65%.

Величина смертности, например выраженная процентом умерших за год в отношении к числу всех жителей, еще сильнее рождаемости изменяется по странам, временам, народам и обстоятельствам, особенно изменчиво распределение смертности в детском возрасте. Процент смертности лиц известного возраста быстро падает, начиная от самого рождения, так что смертность в норме повсюду в первый год после рождения очень велика, даже не считая мертворожденных. Общий же процент смертности на 100 жителей, т. е. количество лиц всех возрастов, умерших в течение года, изменяется от 3,5% в России до 1,7% в Скандинавии. В Германии, где смертность была до 1890 г. близка к 2,6% (ук. соч.), числа рождаемости, смертности и прироста так быстро изменяются за последнюю половину XIX в., что достойны особого внимания:

Германия,год	Миллионов жителей	% рождений	%смертности	% годового прироста
естественного	действительного
	35,4	3,8	2,6	1,2	0,6
	36,1	3,3	2,9	0,4	0,4
	37,7	3,8	2,5	1,3	0,98
	39,7	3,9	2,9	1,0	1,0
	40.8	4,0	2,9	1,1	0,6
	42,7	4,2	2,9	1,3	0,9
	45,2	3,9	2,7	1,2	1,1
	46,9	3,8	2,7	1,1	0,7
	49,4	3,7	2,6	1,1	1,1
	52,3	3,7	2,3	1,4	1,1
	50,7	3,7	2,2	1,5	1,4

Дата добавления: 2015-06-26