
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теоретия метода
|
|
|
|
И СИЛЫ ТРЕНИЯ ОПОРЫ
МОМЕНТА ИНЕРЦИИ МАХОВИКА
ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ
ЛАБОРАТОРНАЯ РАБОТА № 1.8 Б
Цель работы - изучение основных законов динамики поступательного и вращательного движения твердого тела, определение момента инерции маховика.
Движение центра масс твердого тела описывает второй закон Ньютона
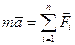 , (1)
, (1)
где т - масса тела; а - ускорение центра масс; 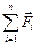 - вектор сумма всех сил, приложенных к телу.
- вектор сумма всех сил, приложенных к телу.
Вращение тела относительно неподвижной оси описывается основным уравнением динамики вращательного движения, которое в проекции на ось вращения 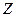 имеет вид
имеет вид
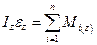 , (2)
, (2)
где 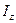 и
и  соответственно момент инерции, и угловое ускорение твердого тела относительно неподвижной оси вращения Z;
соответственно момент инерции, и угловое ускорение твердого тела относительно неподвижной оси вращения Z; 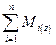 - алгебраическая сумма проекций моментов внешних сил на ось вращения. Относительно неподвижной оси Z момент инерции твердого тела определяется по формуле
- алгебраическая сумма проекций моментов внешних сил на ось вращения. Относительно неподвижной оси Z момент инерции твердого тела определяется по формуле
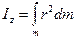 , (3)
, (3)
где 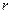 - расстояние от элемента тела массой dm до оси Z
- расстояние от элемента тела массой dm до оси Z
Из формулы (3) следует, что момент инерции зависит от массы тела и от ее распределения относительно оси вращения, т.е. положения оси вращения тела. Момент инерции является мерой инертности тела во вращательном движении.
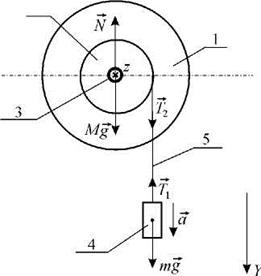
| Рассмотрим маховик (рис. 1), состоящий из диска 1 и шкива 2, которые насажены на общий вал 3, так что система может вращаться относительно оси Z. Маховик - массивное тело (обычно в виде диска, кольца, цилиндра), которое может вращаться относительно некоторой неподвижной оси (обычно это ось симметрии, проходящая через центр масс тела). Особенностью маховика является большое значение его момента инерции относительно оси вращения. Поэтому, чтобы за короткое время привести его в движение или изменить угловую скорость вращения, необходимо приложить значительный момент внешней силы относительно этой оси. Момент инерции маховика можно измерить, изучая его вращение. |
|
| Рис. 1. Схема системы маховик-груз |
Вращение осуществляется под действием груза 4 массой т, подвешенного на нити 5, намотанной на шкив 2 (рис. 1).
Так как моменты силы реакции в оси N и силы тяжести маховика Mg относительно оси вращения равны нулю, то уравнение динамики вращательного движения в проекции на ось Z имеет вид
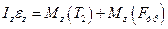 (4)
(4)
Здесь Mz (Т2) - проекция момента силы натяжения нити на ось Z; 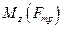 - проекция момента силы трения, приложенной к валу.
- проекция момента силы трения, приложенной к валу.
Учитывая, что 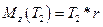 , а также знаки проекций моментов сил Т2 и
, а также знаки проекций моментов сил Т2 и 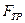 на ось вращения Z получаем
на ось вращения Z получаем
 (5)
(5)
где 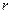 - радиус шкива.
- радиус шкива.
Поступательное движение груза 4 массой m описывается вторым законом Ньютона
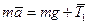
где а - ускорение центра масс груза, 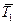 - сила натяжения нити, приложенная к грузу. В проекции на ось Y это уравнение принимает вид
- сила натяжения нити, приложенная к грузу. В проекции на ось Y это уравнение принимает вид
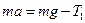 . (6)
. (6)
Предполагается, что нить нерастяжима, поэтому ускорение всех точек нити и груза одинаковы. В отсутствии проскальзывания нити линейное (тангенциальное) ускорение обода шкива равно ускорению груза. Если считать нить невесомой, то силы натяжения нити 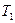 и
и 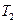 равны между собой
равны между собой 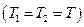 .
.
В процессе движения всей системы груз опускается с постоянным ускорением а с высоты 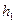 до наинизшего (нулевого) уровня, определяемого длиной намотанной на шкив нити. Тогда, очевидно,
до наинизшего (нулевого) уровня, определяемого длиной намотанной на шкив нити. Тогда, очевидно,
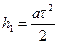 , (7)
, (7)
где 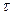 - время за которое груз проходит расстояние
- время за которое груз проходит расстояние 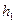 .
.
Так как ускорение поступательного движения груза связано с угловым ускорением вращения маховика соотношением
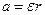
то можем записать
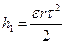 (8)
(8)
Выражение для момента инерции маховика получаем из уравнения (5)
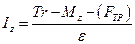 (9)
(9)
Если силу натяжения нити выразить из соотношения (6), а угловое ускорение 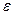 - из (8), то выражение (9) приобретает вид
- из (8), то выражение (9) приобретает вид
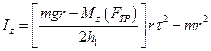 (10)
(10)
Для расчета момента инерции 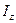 нужно знать все величины, входящие в формулу (10). Из проведенного эксперимента можно измерить
нужно знать все величины, входящие в формулу (10). Из проведенного эксперимента можно измерить 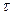 и
и 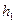 Момент силы трения
Момент силы трения 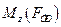 определяем, проведя второй эксперимент. Для этого, вращая маховик, груз поднимают на первоначальную высоту
определяем, проведя второй эксперимент. Для этого, вращая маховик, груз поднимают на первоначальную высоту 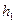 а затем систему предоставляют самой себе. Груз сначала опустится на расстояние
а затем систему предоставляют самой себе. Груз сначала опустится на расстояние 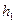 до нижней точки (нить при этом сматывается со шкива), а затем (когда нить начинает наматываться на шкив) поднимается на высоту h2, меньшую чем
до нижней точки (нить при этом сматывается со шкива), а затем (когда нить начинает наматываться на шкив) поднимается на высоту h2, меньшую чем 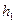 . Причиной подъема груза на меньшую высоту является трение в подшипниках вала.
. Причиной подъема груза на меньшую высоту является трение в подшипниках вала.
Изменение механической энергии системы 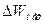 равно работе силы трения
равно работе силы трения 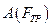
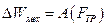 (11)
(11)
Так как начальная и конечная кинетические энергии  и Wk2 равны нулю, то изменение механической энергии системы равно изменению только потенциальной энергии груза
и Wk2 равны нулю, то изменение механической энергии системы равно изменению только потенциальной энергии груза
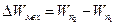 (12)
(12)
Работа силы трения выражается через момент силы трения  и угловое перемещение маховика
и угловое перемещение маховика 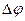
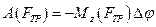 (13)
(13)
Приравнивая правые части уравнений (12) и (13), получаем
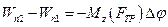 (14)
(14)
или
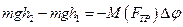
Угловое перемещение маховика 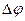 равно отношению длины дуги,
равно отношению длины дуги, 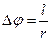 ,
,
которую опишут точки обода шкива за все время движения к его радиусу, где 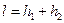 .
.
Подставляя угловое перемещение 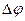 в уравнение (14), получаем
в уравнение (14), получаем
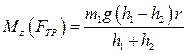 (15)
(15)
Окончательное выражение для определения экспериментального значения момента инерции маховика приобретает вид
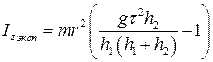 (16)
(16)
Формула (16) позволяет рассчитать момент инерции маховика по измеренным в опытах значениях 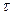 ,
, 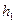 и
и 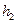 .
.
Значение момента инерции маховика, полученное экспериментально, можно сравнить с теоретическим значением момента инерции вращающейся системы. В данной лабораторной установке маховик можно условно разбить на отдельные элементы: диск, шкив и вал. Поскольку момент инерции твердого тела обладает свойством аддитивности, то можно записать
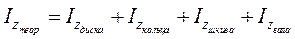
Так масса шкива существенно меньше массы других элементов маховика, и при этом диаметр шкива относительно мал, то моментом инерции шкива 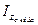 можно пренебречь.
можно пренебречь.
Поэтому
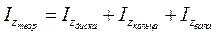
или
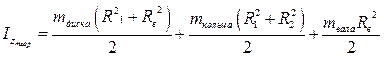 (17)
(17)
где 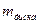 ,
, 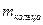 ,
, 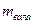 - соответственно массы диска и вала;
- соответственно массы диска и вала; 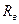 - радиус вала;
- радиус вала; 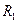 - внешний радиус диска, он же внутренний радиус кольца;
- внешний радиус диска, он же внутренний радиус кольца; 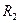 - внешний радиус кольца. Соответствующие параметры представлены в данных установки на экспериментальном стенде.
- внешний радиус кольца. Соответствующие параметры представлены в данных установки на экспериментальном стенде.
|
|
|
|
|
Дата добавления: 2015-06-26; Просмотров: 596; Нарушение авторских прав?; Мы поможем в написании вашей работы!