
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теория метода
|
|
|
|
ИЗУЧЕНИЕ ЗАКОНОВ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА МАЯТНИКЕ ОБЕРБЕКА
ЛАБОРАТОРНАЯ РАБОТА № 1.8А
Цель работы: изучение зависимости момента инерции маятника
от распределения массы в пространстве и проверка уравнения динамики вращательного движения
Приборы и принадлежности: прибор Обербека, секундомер,
измерительная линейка (рулетка).
Рассмотрим движение системы тел, изображенной на рис.1. Крестовина (маятник) с закрепленными на ней грузами массой 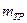 каждый может вращаться вокруг неподвижной горизонтальной оси. Момент инерции крестовины без грузов
каждый может вращаться вокруг неподвижной горизонтальной оси. Момент инерции крестовины без грузов 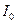 . На блок намотана невесомая нерастяжимая нить, на которой закреплен груз массой т. При движении груза нить разматывается, и крестовина вращается с постоянным ускорением.
. На блок намотана невесомая нерастяжимая нить, на которой закреплен груз массой т. При движении груза нить разматывается, и крестовина вращается с постоянным ускорением.
Движение системы описывается основным уравнением вращательного
движения и вторым законом Ньютона. Уравнение вращательного движения
относительно оси Z, совпадающей с осью вращения и направленной на рис.
1 от нас, имеет вид
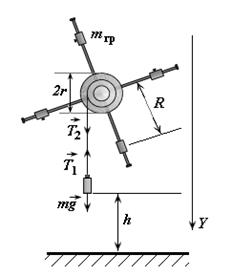
| 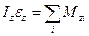 , (8)
где , (8)
где 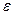 - угловое ускорение маятника; - угловое ускорение маятника; 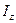 - его момент инерции относительно оси вращения, включающий момент инерции крестовины и момент инерции грузов; - его момент инерции относительно оси вращения, включающий момент инерции крестовины и момент инерции грузов; 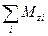 - алгебраическая сумма моментов всех сил относительно оси Z.
В данной работе на шкив наматывается нить, к концу которой привязана гиря известной массы m. При падении гири сила натяжения нити T создает момент относительно оси вращения
M = Tr i, (8а)
Второй закон Ньютона для тела массой т - алгебраическая сумма моментов всех сил относительно оси Z.
В данной работе на шкив наматывается нить, к концу которой привязана гиря известной массы m. При падении гири сила натяжения нити T создает момент относительно оси вращения
M = Tr i, (8а)
Второй закон Ньютона для тела массой т
|
| Рис. 1 |
запишем в проекции на ось OY
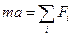 , (9)
, (9)
здесь а - ускорение поступательного движения груза массой т; 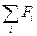 - алгебраическая сумма проекций всех сил, приложенных к грузу. На груз т действует сила тяжести mg и сила натяжения нити
- алгебраическая сумма проекций всех сил, приложенных к грузу. На груз т действует сила тяжести mg и сила натяжения нити 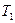 .
.
Поскольку нить невесома, поэтому силы натяжения нити 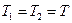 . Следовательно, силу Т можно найти из уравнения поступательного движения гири:
. Следовательно, силу Т можно найти из уравнения поступательного движения гири:
ma = mg - T, (9а)
где m масса гири, а его ускорение. Из этих уравнений получаем, что момент силы натяжения нити
С учетом того, что на маятник действуют момент силы натяжения нити 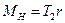 и момент силы трения
и момент силы трения 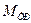 в подшипниках, выражение (1) можно представить в виде
в подшипниках, выражение (1) можно представить в виде
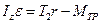 . (10)
. (10)
Из этих уравнений (8а) и (9а) получаем, что момент силы натяжения нити
M = m (g - a) r. (10а)
Остальные внешние силы (сила тяжести маятника и сила реакции опоры) вращающего момента не создают, поскольку их линия действия пересекает ось вращения. Перераспределив массы на крестовине маятника, можно повторить опыты, и определить новые значения момента инерции Iz и момента силы натяжения нити M = m (g - a) r (момент силы 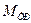 трения измениться не должен), который приводит к вращению системы.
трения измениться не должен), который приводит к вращению системы.
Если нить нерастяжима и нет проскальзывания между нитью и блоком, то ускорение поступательного движения груза и угловое ускорение маятника связаны соотношением 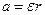 С учетом этих дополнительных соотношений из (3) и (4) можно получить выражения для различных физических величин.
С учетом этих дополнительных соотношений из (3) и (4) можно получить выражения для различных физических величин.
Определим соотношения, по которым из опыта с маятником Обербека можно легко рассчитать угловое ускорение маятника ε и момент силы 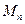 .Кинематический закон движения груза
.Кинематический закон движения груза 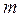 связывает высоту падения груза h, линейное ускорение а, и время движения груза t:
связывает высоту падения груза h, линейное ускорение а, и время движения груза t: 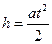 . В случае плотной намотки нерастяжимой нити ускорение, а связано с угловым ускорением ε соотношением ε = a / r. Ускорение, а можно определить, измеряя время t i, в течение которого груз опускается на расстояние h:
. В случае плотной намотки нерастяжимой нити ускорение, а связано с угловым ускорением ε соотношением ε = a / r. Ускорение, а можно определить, измеряя время t i, в течение которого груз опускается на расстояние h:
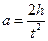 (11)
(11)
Тогда 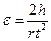 (12)
(12)
Решая эти уравнения совместно, и учитывая, что 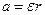 , можно получить следующее выражение для момента силы натяжения
, можно получить следующее выражение для момента силы натяжения
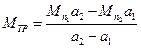 (13)
(13)
С учетом выражений (5) и (7), формула для момента силы трения перепишется в виде
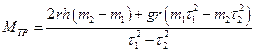 (14)
(14)
Из уравнений (8) и (9) можно также определить момент инерции маятника Обербека:
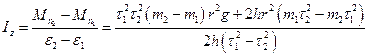 (15)
(15)
|
|
|
|
|
Дата добавления: 2015-06-26; Просмотров: 400; Нарушение авторских прав?; Мы поможем в написании вашей работы!