Двумерные корреляционные функции

Для описания корреляционных свойств геофизических полей, измеренных по площади съемки, используется двумерная автокорреляционная функция (ДАКФ), которая для центрированных значений поля, т.е. при равенстве средних значений каждого профиля нулю, определяется выражением

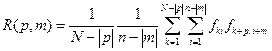(4.11)

где 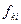- центрированные по всей площади наблюдения значение поля (из значений поля вычитается среднее по всей площади значение) на k -ом профиле в i -той точке, индекс p – смещение между профилями съемки: 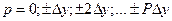; индекс m – смещение вдоль профиля 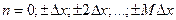; N – общее число профилей; n – число точек по профилю.

Для изучения структуры ДАКФ распишем выражение (4.11) для различных фиксированных значений p.

При р =0 получаем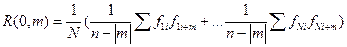

Т.е. при р =0 ДАКФ представляет сумму всех одномерных АКФ, вычисленных для значений каждого профиля и осредненный по общему числу профилей N.

При р =1 имеем: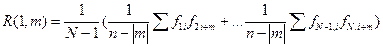

Т.е. при р =1 ДАКФ равна осредненной сумме ВКФ, вычисленных для значений поля данных соседних пар профилей.

При р =2 ДАКФ равна осредненной ВКФ, вычисленных для значений поля данных, расположенных через профиль и т.д.

Построение ДАКФ в изолиниях ее рельефа на плоскост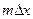и и 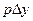позволяет наглядно отображать корреляционные свойства геофизических наблюдений по площади.

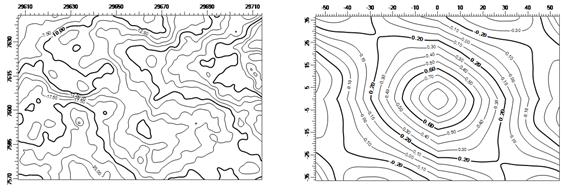
На рис.4.3 приведены результаты наблюденного гравитационного поля и соответствующая ему ДАКФ. Применение ДАКФ аналогично применению одномерной АКФ, но в дополнение к перечисленным в разделе 4.1 задачам обработки, по ДАКФ возможна оценка простирания сигналов различного простирания

Рис.4.3. Гравитационное поле dG (слева) и его двумерная автокорреляционная функция (справа).

Центральная симметрия ДАКФ проявляется в равенствах 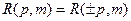и 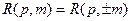, т.е. расчеты ДАКФ достаточно осуществить лишь для положительных значений р или для положительных значений m.

Двумерная взаимно корреляционная функция (ДВКФ) рассчитывается как для положительных, так и для отрицательных значений m и p по формуле

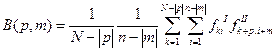(4.12)

где 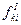и 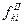- центрированные по всей площади наблюдения значения двух разных полей, либо значения полей, полученных на различных глубинах залегания или на разных высотах.

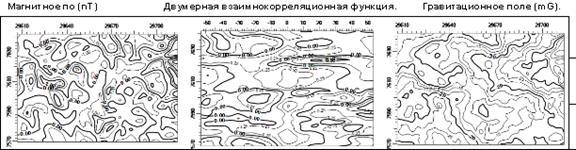
ДВКФ характеризует взаимные корреляционные свойства, либо разных полей, либо полей, полученных на разных высотах и глубинах. На рисунке 4.4. приведена ДВKФ между магнитным и гравитационным полями.

Рис.4.4.Двумерная взаимно-корреляционная функция (в центре) между магнитным полем dT (слева) и гравитационным полем dG (справа).

Помимо авто- и взаимно корреляционных функций в практике обработки геофизических данных нашли применение такие корреляционные функции, как:

Структурная функция 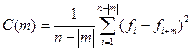, используемая при обработке геохимических данных. Для структурной функции формируются и взаимно-структурные функции. Ретрокорреляционная функция 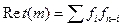, используется при выделении кратных волн в сейсморазведке.

ГЛАВА V. СПЕКТРАЛЬНЫЙ АНАЛИЗ ГЕОФИЗИЧЕСКИХ СИГНАЛОВ.

Спектральный анализ занимает центральное место при обработке геофизических данных. Спектральный анализ используется для описания спектрального (частотного) состава геофизических сигналов, заданных как детерминированными, так и случайными функциями.

В настоящее время спектральный анализ объединяет методы анализа Фурье и статистический анализ временных последовательностей наблюдений. Под анализом Фурье понимается разложение сигнала по периодическим функциям синусов и косинусов. Спектр – это функция, описывающая распределение амплитуд и фаз по различным частотным составляющим (гармоникам) сигнала, начиная с низкочастотных и кончая высокочастотными составляющими. Суммирование частотных составляющих с учетом их амплитуд и фаз приводит к восстановлению формы сигнала.

Практическое применение анализа Фурье при обработке геофизических данных связано с их представлением в виде сигналов, заданных в дискретных точках наблюдений, т.е. 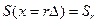или 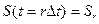поскольку обработка данных проводится на ЭВМ, где все данные – дискретны.

Анализ Фурье предназначен для обработки периодических сигналов, для которых выполняется соотношение 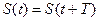, где Т называется периодом сигнала. Для непериодических сигналов, например, 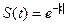такого периода не существует, и при анализе Фурье подобных сигналов период задается искусственно, ограничивая непериодический сигнал величиной Т при малых его значениях. В теоретических приложениях рассматриваются апериодические сигналы, для которых период стремится к бесконечности т.е. .

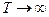При спектральном анализе Фурье основными типами сигналов являются: дискретные и непрерывные, периодические и непериодические, детерминированные (аналитически заданные) и случайные.

Дата добавления: 2015-06-26