Метод динамических сгущений (k-средних)

Методы классификации многомерных наблюдений.

Существующие в настоящее время классификационные алгоритмы, основанные на принципах самообучения, можно разделить на три основных группы – эвристические, корреляционные и статистические. Эвристические методы классификации основаны на разбиении диапазона значений каждого признака на заданное число градаций и в большинстве своем сводятся к расчету комплексного параметра, который является линейной комбинацией соответствующего номера интервала градации по совокупности анализируемых признаков в каждой точке наблюдений. Существенным недостатком эвристических методов является то обстоятельство, что они строятся в предположении независимости отдельных признаков между собой. Однако, наличие отдельных недостатков алгоритмов классификации не уменьшает их значимости в обработке геолого-геофизических наблюдений.

Рассматриваемые способы классификации многопризнаковых геофизических наблюдений относятся к числу эвристических и направлены на решение задачи выделения в многомерном пространстве компактных групп точек. В прикладных задачах автоматической классификации (при отсутствии эталонных объектов) эвристические алгоритмы стали применяться одними из первых и до сих пор сохраняют большое значение благодаря наглядности полученных результатов и, как правило, простоте реализации.

Разделение рассматриваемой совокупности признаков на однородные (в смысле вектора среднего) группы называется классификацией. При этом термин “классификация” используют, в зависимости от контекста, для обозначения, как самого процесса разделения, так и его результата. Это понятие тесно связано с такими терминами, как группировка, типологизация, систематизация, дискриминация, кластеризация, и является одним из основополагающих в практической и научной деятельности человека.

В общей постановке задачи проблема классификации объектов заключается в том, чтобы всю анализируемую совокупность признаков, представленную в виде матрицы, разбить на сравнительно небольшое число однородных, в определенном смысле, групп или классов. Понятие однородности основано на предположении, что геометрическая близость двух или нескольких объектов означает близость их “физических” состояний, их сходство.

В общем случае понятие однородности объектов определяется заданием правила вычисления величины r_ij. характеризующей расстояние 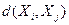между объектами Х_i и Х_j из исследуемой совокупности. Если задана функция 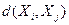. то близкие в смысле этой метрики объекты считаются однородными, принадлежащими к одному классу. Естественно, при этом необходимо сопоставление 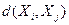с некоторым пороговым значением, определяемым в каждом конкретном случае по-своему.

Достаточно известный и эффективный метод классификации многомерных наблюдений на заранее известное число классов 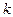в условиях минимума информации о начальных центрах классов, известный под названием k -средних или k -ближайших соседей. Блок схема алгоритма заключается в следующем:

-для всех 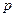обрабатываемых признаков оценивается значение среднеквадратического отклонения 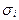, минимального 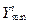и максимального 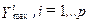значений;

-каждый 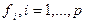признак нормируется на соответствующее значение среднеквадратического отклонения ;

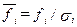-случайным образом выбирается 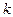векторов размерности 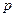начальных центров классов 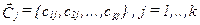. причем отдельные случайно выбранные компоненты каждого вектора удовлетворяют неравенству ;

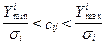-осуществляется классификация нормированных многопризнаковых наблюдений исходной сети на классы, при этом значение в каждой точке сети 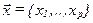относится к классу 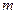. если расстояние от центра этого класса до точки является минимальным ;

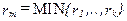-по результатам классификации определяются новые вектора центров классов. 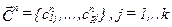. при этом каждая компонента отдельного вектора 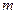является оценкой среднего 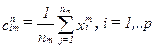. рассчитанной по 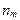точкам, попавшим в класс 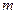после классификации. проведенной на предыдущем шаге алгоритма;

-в выбранной метрике оцениваются расстояния между старыми и новыми центрами классов ;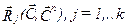

-если хотя бы для одного из 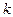классов расстояние больше заранее выбранной величины 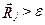. то старым векторам центров классов присваиваются значения новых 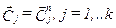и процедура повторяется с шага, на котором осуществляется классификации наблюдений. В противном случае, когда для всех классов выполняется неравенство 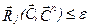, результаты последней итерации считаются окончательными.

Рассмотренный итерационный алгоритм обладает довольно быстрой сходимостью. Основным его недостатком является недостаточный учет корреляционных связей признакового пространства и необходимость задания конечного числа классов.

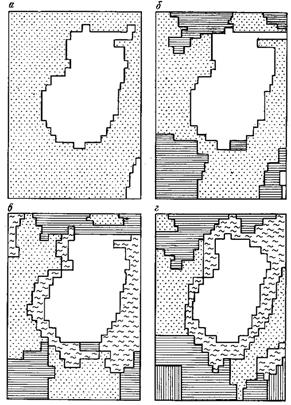
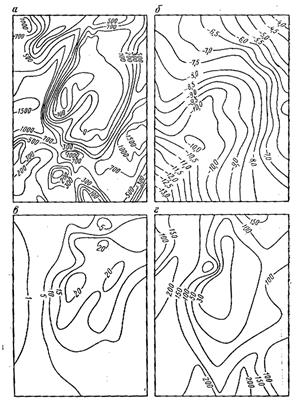
Рис.9.1.Геофизические поля над Бенкалинским меднопорфировым месторождением: а) Za в nT, б) ∆g в mG, в) - hk в %, г) rk в Ом×м.	Рис.9.2.Результат классификации геофизических полей методом к-средних на два а), три б), четыре в) и пять г) классов.

Дата добавления: 2015-06-26