Метод главных компонент при расчете комплексного параметра

Методы распознавания образов в задачах интерпретации геофизических наблюдений.

Метод разделения многомерных, нормальных смесей

(По Петрову А.В.).

Алгоритм, позволяет провести классификацию многопризнаковых геофизических наблюдений на однородные, в смысле вектора среднего области, без знания конечного числа классов и с учетом корреляционных характеристик всего признакового пространства.

Алгоритм построен на принципах самообучения и позволяет решать задачу разделения сейсмического разреза на области с одинаковым значением вектора среднего по совокупности признаков. Конечное число классов (однородных в смысле вектора среднего областей) определяется автоматически в процессе работы алгоритма. Суть алгоритма заключается в следующем.

Считается, что вся совокупность наблюдений, включающая M трасс по N отсчетов на каждой, может быть разбита на J областей, в которых данные распределены многомерно нормально с вектором математического ожидания 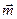и матрицей ковариаций S. Размерность векторов 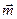и матрицы S совпадает с количеством анализируемых признаков p. Относительно ковариационной матрицы S предполагается, что она постоянна во всех областях. Вектора среднего 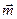для различных областей отличаются друг от друга, то есть

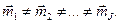
Число таких областей J ‑ неизвестно. Естественно, что оно не может быть меньше единицы (J>0) (в случае равенства единице все данные относятся к одной области, классу) и не превышает общего числа точек наблюдений J³MN=n (в случае равенства каждая область содержит только лишь один объект наблюдения, то есть точку). Задача заключается в разбиении исследуемой площади наблюдений на области, однородные в смысле вектора среднего, по всем признакам.

Для решения этой задачи предлагается алгоритм, основанный на проверке многомерной статистической гипотезы, в котором можно выделить два основных этапа:

1.На первом этапе проверяется гипотеза о принадлежности двух различных областей к одному классу. Первоначально считается, что число таких областей равно количеству точек наблюдений, то есть каждая точка ‑ класс. При этом, если два проверяемых класса удовлетворяют этой гипотезе на определенном уровне значимости, то они объединяются в один класс. Первоначальное число классов уменьшается на единицу и пересчитывается оценка ковариационной матрицы S, которая имеет важнейшее значение для расчета статистики критерия, соответствующего данной гипотезе. Этап завершается, когда гипотеза об объединении всевозможных пар классов не выполняется.

2.Второй этап заключается в реклассификации данных, разделенных на классы в результате первого этапа. Затем проводится повторение первого этапа, но при этом с самого начала в статистике критерия для проверки гипотезы объединения двух различных классов уже используется оценка ковариационной матрицы S, полученная на первом этапе обработки.

Как следует из структуры описанного алгоритма для его реализации необходимо получить многомерный статистический критерий для проверки гипотезы о том, что два любых класса m и l из J существующих, обладают одним и тем же вектором среднего, то есть гипотезу

В работе [5] подробно описывается построение критериальной статистики для проверки сформулированной выше гипотезы, поэтому ниже приводится лишь окончательное выражение:

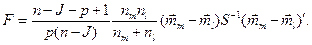
здесь n ‑ общее число точек;

n_m и n_l – число точек в проверяемых классах;

J – общее число классов;

p –число анализируемых признаков;

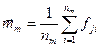‑ оценка вектора среднего в m ‑ом классе;

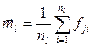‑ оценка вектора среднего в l ‑ом классе;

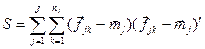- оценка ковариационной матрицы по всем классам;

n_j - число точек в j –ом классе.

Гипотеза H₁ о равенстве векторов средних в классах l и m считается справедливой на уровне значимости a. если выполняется неравенство: где ‑ критическое значение F ‑ распределения со степенями свободы: g₁ = p. g₂=n-J-p+1.

Одной из актуальных задач разведочной геофизики является выделение геологического объекта по информации о параметрах полей, которые им индуцируются. Подобные задачи возникают при геолого-геофизическом районировании, обработке многоуровневых геофизических наблюдений и в других случаях, когда при интерпретации наблюденное поле сравнивается с эталонным фрагментом поля.

Существует ряд алгоритмов распознавания по данным комплексных геолого-геофизических наблюдений, в которых решение задачи коротко сводится к следующему. Первоначально проводится обучение на эталонных объектах по ряду геолого-геофизических признаков с целью оценки тех или иных параметров признаков. Затем по имеющейся информации о значениях параметров признаков в каждой точке площади исследования делается вывод о принадлежности точки к эталонному объекту. Этап обучения на эталонных объектах является одним из самых уязвимых мест рассматриваемых методов распознавания. Многообразие геолого-геофизической информации, обусловленное изменением геологического строения в пределах даже одной площади, влияние различного рода помех очень часто не позволяют использовать результаты обучения на эталонных объектах для решения задач распознавания на других площадях со сходным геологическим строением.

В наибольшей степени сказанное проявляется при включении в процесс распознавания геофизических наблюдений. Именно поэтому геофизическая информация обычно используется далеко не полностью и сводится чаще всего к таким параметрам, как знак аномалии, значение величины среднего, степень изменчивости полей (дисперсия) и их производных.

Параметрами, характеризующими эталонный объект для предлагаемого алгоритма, являются двумерные поверхности, заданные в дискретных точках наблюдений прямоугольной сети. Каждая поверхность отражает форму проявления конкретного физического поля над эталонным объектом. Признаками могут быть значения различных геофизических полей, их производные, наблюдения на различных уровнях одного геофизического параметра, оцифрованная геологическая, петрофизическая и геохимическая информация. При построении алгоритма принимается аддитивная модель поля, при которой любое наблюдение является суммой комплексной аномалии и многомерной нормальной с нулевым вектором среднего помехи.

Существо предлагаемого алгоритма состоит в следующем. Без ограничения общности рассмотрим прямоугольное окно на анализируемой площади наблюдений размером т профилей и n пикетов и наклоном q =0. Пусть в каждой i -ой точке окна наблюдения являются р - мерными величинами (р— число анализируемых признаков) fi= (f₁. f₂..... f_р), причем: f_i=a_i+n_i, где a_i - аномальная составляющая поля, n_i- многомерная нормальная помеха с нулевым вектором среднего и матрицей ковариаций S.

Очевидно, при совпадении формы комплексной аномалии в исследуемом окне от эталонного объекта a с наблюденным полем x, разность между ними есть не что иное, как помеха:

d_kj= x_kj- a_kj где. k=1.2....... m; j=1.2....... п.

где m – количество строк в окне, а n –количество столбцов.

Таким образом, решение вопроса распознавания комплексной аномалии от эталонного объекта сводится к проверке нулевой гипотезы H₀ о том, что значения разности d в столбцах и строках окна распределены нормально с нулевым вектором среднего и ковариационной матрицей S. т. е.

m₁=m₂=.... m_m= m_m+1 =.....=m_m+n

где m_k. k=1....m - вектор среднего разности d в строках окна;

j=1....n— вектор среднего разности d в столбцах окна.

Окончательное выражение для проверки гипотезы H₀ [4] имеет вид:

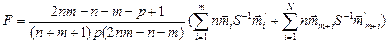
здесь

-оценка вектора среднего разности в j-ой строке окна j=1.....m;

-оценка вектора среднего разности в i-ом столбце окна i=1.....n.

S - оценка ковариационной матрицы в окне.

Гипотеза Н₀ о наличии в окне эталонной комплексной аномалии считается справедливой на уровне значимости а. если выполняется неравенство F<F g _{1. g2}.a. а. где Fg₁.g₂.a -критическое значение F -распределения со степенями свободы g₁ и g₂

.

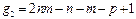Перемещая окно вдоль профиля и по профилям, получим распределение критериальной. статистики по всей площади наблюдения.

При использовании рассмотренного способа распознавания комплексных геофизических аномалий эталонную аномалию по комплексу признаков можно получить путем обучения на площадях с известным геологическим строением, либо путем решения прямой задачи по каждому признаку, а также создав банк элементарных аномалий, из которых путем линейных преобразований и различных комбинаций по признакам можно быстро получать комплексную аномалию с заданными энергией и геометрией. За эталонную аномалию можно принять фрагмент исследуемой площади с целью поиска аналогичных участков на всей площади. Особый интерес представляет распознавание при различных наклонах окна, так как при этом выделяются области в которых присутствует эталонный объект при различных его простираниях. Основные достоинства рассмотренного метода распознавания заключаются в следующем:

1.Алгоритм базируется на проверке многомерной статистической гипотезы, что позволяет наиболее полно использовать информацию о структуре межпризнаковой связи между различными геофизическими полями.

2.Исходной информацией является лишь форма аномалий, а в ряде случаев, когда эталоном служит фрагмент исследуемой площади, лишь контур комплексной аномалии. Оценка параметров помехи и ее влияния на полезный сигнал проводятся непосредственно в процессе распознавания.

3.В качестве признаков над эталонным объектом выступают геофизические поля, что позволяет наиболее полно учесть все их особенности при обработке.

4.Возможность изменения наклона окна делает алгоритм независимым от простирания объекта.

5.Независимость алгоритма от характера помех и применение банка элементарных аномалий значительно сокращают этап обучения и повышают мобильность алгоритма при обработке различных исследуемых территорий.

Основные недостатки метода сводятся к возможному невыполнению на практике предпосылок, заложенных в математической модели, а именно: принимаемая аддитивная модель наблюдаемого поля, предположение о нормальном распределении помехи и стохастическая независимость наблюдений.

Исходными данными при комплексном анализе является совокупность нескольких полей и (или) их атрибутов в виде Nn -точек наблюдений. Алгоритм метода главных компонент сводится к реализации следующих процедур:

1.Вычисление коэффициентов корреляции 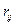для случайных величин и и составление по коэффициентам корреляции корреляционной матрицы

.

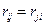
2.Составление матрицы . где I -единичная матрица, и приравнивание определителя матрицы к нулю, т.е.

3.Раскрытие определителя в виде линейного уравнения относительно 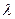и нахождение корней этого уравнения, являющихся собственными значениями матрицы .

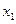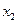Например, для двух случайных величин и имеем

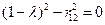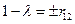; . т.е. ; .

Очевидно, что для матрицы R размерности N получим N собственных ее значений.

4.Нахождение собственных векторов матрицы R путем решения системы линейных уравнений вида:

т.е.

Для определенности решения этой системы необходима указанная выше нормировка коэффициентов в виде .

В результате решения системы линейных уравнений для каждого собственного значения 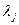получаем свой собственный вектор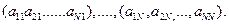

Система собственных векторов является ортогональной и корреляционная матрица R оказывается расщепленной на N -ортогональных компонент.

5.Вычисление первой главной компоненты 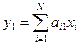, соответствующей максимальному собственному значению 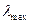. 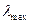равно дисперсии первой главной компоненты, отражающей 70-90% всей энергии. т.е. .

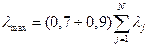Первая главная компонента представляет значения комплексного параметра, определяемого в n-точках наблюдений, поскольку 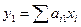выражается в виде произведения исходной матрицы x на собственный вектор, соответствующий максимальному собственному значению:

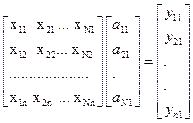
Физический смысл весовых коэффициентов 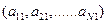состоит в том, что эти коэффициенты определяют «вес» (вклад) каждого поля в общую величину комплексного параметра или информативность исходных полей.

Заметим, что случайная природа полей практически в методе главных компонент не используется, поэтому все перечисленные выше процедуры можно использовать и для аналитических, детерминированных функций. Так, в метеорологии метод главных компонент получил название как метод естественных ортогональных функций.

ЗАКЛЮЧЕНИЕ.

В заключении отметим, что в процессе изучения материала по курсу «Теоретические основы обработки геофизической информации» следует использовать программные средства по соответствующим разделам, что способствует лучшему усвоению достаточно сложных теоретических основ.

В качестве подобных программных продуктов можно рекомендовать пакет «МАТLAB». В РГГРУ под руководством профессора Петрова А.В. разработаны обучающая система «Геостат» и компьютерная технология «КОСКАД 3D». Последняя включает шесть основных разделов:

«Сервис» -обеспечивает выполнение стандартных функций системы управления базой данных. С их помощью осуществляется ввод/вывод содержательной информации, объединение и фрагментация сетей, восполнение отсутствующих в отдельных точках наблюдения значений признака, интерполяция сетей, различные преобразования с данными и т.д.

«Графика» - включает графический интерфейс, позволяющий оперативно просматривать одномерную, двумерную и трехмерную информацию из базы данных на экране дисплея в виде растровых карт, отдельных графиков, карт графиков и т.д..

«Статистика» - программы данного раздела предназначены для расчета статистических, спектральных и корреляционных характеристик геополей. Анализ этих характеристик позволяет получить дополнительную, полезную информацию об исследуемом поле и правильно выбрать граф его дальнейшей обработки.

«Фильтрация» - в модулях данного раздела реализованы наиболее распространенные в разведочной геофизике линейные оптимальные фильтры, позволяющие решать задачи разложения поля на составляющие, исключения тренда, оценки формы слабых аномалий. Особый интерес представляют уникальные адаптивные фильтры, позволяющие корректно обрабатывать нестационарные по спектрально-корреляционным характеристикам геофизические поля.

«Обнаружение» -с помощью программ данного раздела решается задача обнаружения слабых аномалий, соизмеримых по амплитуде с уровнем помех, линейной и изометричной формы, по одному или нескольким признакам.

«Комплекс»- использование программ этого раздела позволяет решать задачи разбиения анализируемой площади на однородные области (классы) с равными средними значениями признаков, распознавания комплексных аномалий по эталонной аномалии. Кроме этого возможно проведение компонентного анализа многопризнаковых данных.

Для программ этой группы в качестве входной информации могут быть использованы значения различных геолого-геофизических признаков и их производных, полученных с помощью программ из других разделов комплекса.

Литература.

Основная:

1.Никитин А.А. Теоретические основы обработки геофизической информации. М.. Недра. 1986.

2.Серкеров С.А. Спектральный анализ гравитационных и магнитных аномалий. М.Недра, 2002 г.

Дополнительная:

3.Петров А.В. Адаптивная фильтрация геополей. Геоинформатика. 1996. № 6.

4.Петров А.В. Распознавание комплексных геофизических аномалий. Геология и разведка. Изв.ВУЗов № 1 1996 г. стр.129.

5.Петров А.В. Методы многомерного дисперсионного анализа в алгоритмах комплексной интерпретации геофизических наблюдений. Геофизика № 1. 1996.

6.Петров А.В.. Никитин А.А. Многомерные аналоги способа обратных вероятностей и самонастраивающейся фильтрации. Геология и разведка Изв. ВУЗов N2 1989 г.

7.Никитин А.А.. Хмелевской В.К. Комплексирование геофизических методов. г.Тверь. Изд. ГЕРС. 2004.

[1] В главе 2 подробно рассматриваются метод наименьших квадратов и вопросы полиномиальной аппроксимации геофизических наблюдений.

[2] Слово correlation переводится с английского языка как схожесть в изменениях, таким образом, под корреляцией понимается степень схожести или связи в изменении двух процессов.

[3] Если из значений случайной величины вычесть ее математическое ожидание (среднее), то полученная таким образом, случайная величина называется центрированной.

[4] Обычно получают достаточно достоверные оценки автокорреляционных функций при N>=30. При этом оценки вычисляются для смещений, не превышающих половины длины реализации (профиля) m<=N/2.

[5] Слово correlation переводится с английского языка как схожесть в изменениях, таким образом, под корреляцией понимается степень схожести в изменениях двух процессов.

[6] что является далеко нетривиальной задачей.

[7] Под базовым окном понимается окно, размер которого не меньше наиболее энергоемких и протяженных аномалий, присутствующих на профиле. По точкам, попадающим в это окно, оцениваются корреляционные характеристики поля в окрестности каждой точки.

[8] Под двумерным базовым окном понимается прямоугольное окно, размеры которого не меньше размеров наиболее энергоемких аномалий.

Дата добавления: 2015-06-26