
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Введение 3 страница. Поверхностные силы. Поверхностные силы определяют так называемое поверхностное «напряжение»
|
|
|
|
Поверхностные силы. Поверхностные силы определяют так называемое поверхностное «напряжение». Поверхностное напряжение определяется выражением:
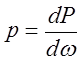 , (2.3.1)
, (2.3.1)
где Р - действующая поверхностная сила,  - площадь взаимодействия поверхностной силы.
- площадь взаимодействия поверхностной силы.
Объемные силы. Объемные силы (массовые силы) определяются воздействие внешних сил. Для них можно записать:
 (3.3.2)
(3.3.2)
2.3.2 Основная теорема гидростатики
Основная теорема гидростатики. Основная теорема гидростатики устанавливает то, что гидростатическое давление (р) в данной точке не зависит от его направления, т.е.:
 , (2.3.3)
, (2.3.3)
.где 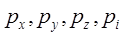 давления по направлению осей координат x,y,z и произвольному направлению i.
давления по направлению осей координат x,y,z и произвольному направлению i.
Рассмотрим некоторый элементарный объем жидкости (рис.2.3.2.) при условии, что он находится в состоянии равновесия. 

Рис. 2.3.2.
В этом случае можно состояние равновесия выразить в виде трех уравнений проекций действующих сил и трех уравнений моментов:
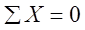 и
и 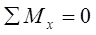
 и
и 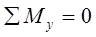
 и
и 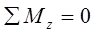 (2.3.4)
(2.3.4)
При уменьшении граней выделенного объема в пределе до нуля система действующих сил превратится в систему сил, проходящих через точку, а система уравнений моментов теряет смысл.
Проекции этих сил на оси x, y, z можно представить в виде:
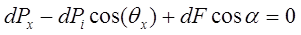

 , (2.3.5.)
, (2.3.5.)
Где 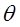 угол между нормальным направлением силы
угол между нормальным направлением силы 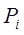 и соответствующей осью координат, а
и соответствующей осью координат, а 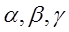 углы между составляющей равнодействующих массовых сил
углы между составляющей равнодействующих массовых сил 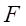 и осями координат.
и осями координат.
Учитывая, что
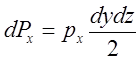 ;
; 
и 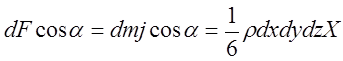 .
.
Проводя подобные рассуждения, относительно проекций сил на другие оси координат, и осуществляя соответствующие преобразования, получим:
 -
-
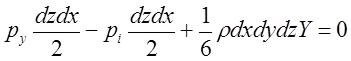 -
-
(2.3.6.)
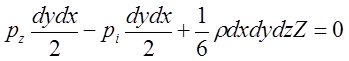
Или, проведя соответствующие преобразования окончательно, получим:
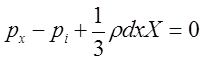

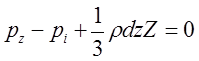
(2.3.7.)
Учитывая, что последняя составляющая в данной системе уравнений, представляет величину высшего порядка малости, можем записать:

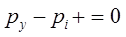

(2.3.8.)
или
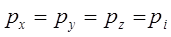
Что и требовалось доказать.
В данном случае было доказано равнозначность гидростатического давления в точке по любому направлению, однако не следует забывать, что давление является функцией координат и времени.
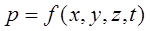
2.3.3 Основной закон гидростатики
Основной закон гидростатики. Выделим в объеме некоторую элементарную площадку 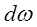 . Данная площадка сверху нагружена столбом жидкости высотою
. Данная площадка сверху нагружена столбом жидкости высотою 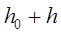 , где
, где 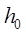 высота столба жидкости (воздуха) над свободной поверхностью жидкости.
высота столба жидкости (воздуха) над свободной поверхностью жидкости.

 Рис.2.3.3.
Рис.2.3.3.
Предполагая, что жидкость находится в состоянии относительного покоя. Выделим элементарный объем рис.2.3.3.
Условие равновесия выделенного элементарного объема предполагает равенство массовых и поверхностных сил. В проекциях на оси x, y, z можем записать:


(2.3.9)

или
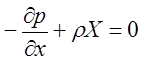
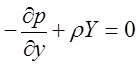 (2.3.9 а)
(2.3.9 а)

Система уравнений (2.3.9 а) описывает относительное равновесное состояние жидкости (система уравнений равновесного состояния жидкости-Эйлера).
Сложение правых и левых частей уравнения позволяет получить уравнение:
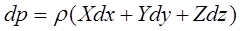 (2.3.10)
(2.3.10)
Уравнение (2.3.10) представляет собой основное уравнение гидростатики.
Уравнение поверхности уровня. Поверхность уровня представляет поверхность равного давления. Поверхность уровня предполагает 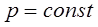 или
или 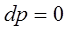
В этом случае уравнении (20) примет вид:
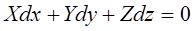 (2.3.11)
(2.3.11)
Уравнение (2.3.11) представляет уравнение поверхности уровня.
Поверхность уровня обладает определенными свойствами:
1. Поверхности уровня не пересекаются.
2. Направление объемных сил нормально к поверхности уровня.
Равновесие жидкости в поле земного тяготения. Рассматривая уравнение (2.3.10) для случая работы его в поле земного тяготения, т.е. X=0, Y=0, а Z=-g (см. рис. 2.3.3). В данном случае уравнение (2.3.10) примет вид
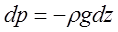 (2.3.12)
(2.3.12)
Проводя интегрирование уравнения (2.3.12) окончательно получим
 , (2.3.13)
, (2.3.13)
где p - величина гидростатического давления столба воздуха над выделенной поверхностью; 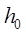 - высота столба воздуха;
- высота столба воздуха;  - высота столба жидкости над выделенной поверхности.
- высота столба жидкости над выделенной поверхности.
Окончательно уравнение (2.3.13) примет вид:
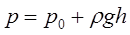 (2.3.13 а)
(2.3.13 а)
2.3.4 Сила давления жидкости на плоские поверхности.
Сила давления жидкости на плоские поверхности. Определим силу давления Pн на произвольную наклонную площадь  (рис.2.3.4). В данном случае величина Pн определяется из соотношения:
(рис.2.3.4). В данном случае величина Pн определяется из соотношения:
 , (2.3.14)
, (2.3.14)
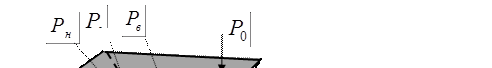
Рис. 2.3.4
Проекции силы Pн на оси x y z можно определить из выражений:

 (2.3.15)
(2.3.15)
 ,
,
где  углы пространственной ориентации силы Pн
углы пространственной ориентации силы Pн
и осей координат xyz.
Центр давления. Центром давления называется точка приложения силы давления в столбе жидкости на расчетную площадку. Центр давления характеризуется координатами xyz, а для плоскости двумя координатами. В этом случае положение центра давления можно определить из выражения
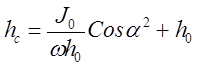 , (2.3.16)
, (2.3.16)
Где  расстояние от поверхности уровня жидкости до точки приложения силы давления;
расстояние от поверхности уровня жидкости до точки приложения силы давления;
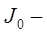 момент инерции площадки
момент инерции площадки  относительно рассматриваемой оси, проходящей через центр тяжести площадки;
относительно рассматриваемой оси, проходящей через центр тяжести площадки;
 расстояние от поверхности уровня жидкости до центра тяжести площадки;
расстояние от поверхности уровня жидкости до центра тяжести площадки;
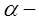 угол ориентации площадки
угол ориентации площадки  .
.
Для рассматриваемого случая, величина,  т.е. центр давления всегда ниже центра тяжести рассматриваемой площадки. Исключение составляет частный случай, когда площадка, расположена горизонтально, в плоскости x o y. В этом случае центр давления совпадает с центром тяжести площадки. Расстояние между центром тяжести и центром давления принимается как эксцентриситетом приложения силы давления и центром тяжести.
т.е. центр давления всегда ниже центра тяжести рассматриваемой площадки. Исключение составляет частный случай, когда площадка, расположена горизонтально, в плоскости x o y. В этом случае центр давления совпадает с центром тяжести площадки. Расстояние между центром тяжести и центром давления принимается как эксцентриситетом приложения силы давления и центром тяжести.
Давление жидкости на криволинейные поверхности. Рассмотрим криволинейную поверхность (рис.2.3.5).
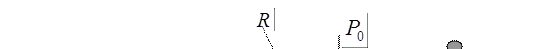
Рис. 2.3.5
Так как поверхность пластины криволинейная, то силы dR образуют систему не параллельных сил. Такую систему можно привести к главному вектору R. В общем случае можем записать:
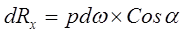
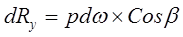 (2.3.17)
(2.3.17)
 ,
,
где  углы пространственной ориентации силы R
углы пространственной ориентации силы R
и осей координат x y z.
Сумма проекций элементарных сил может быть выражена в виде равнодействующей силы R;

 (2.3.18)
(2.3.18)
 ,
,
Сила R по величине будет рана;
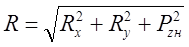 , (2.3.19)
, (2.3.19)
Решение уравнений (28) можно представить в виде:
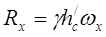
 (2.3.20)
(2.3.20)
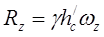 ,
,
где  - глубина погружения центра тяжести площадок, соответственно
- глубина погружения центра тяжести площадок, соответственно 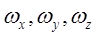 .
.
2.3.5. Закон Архимеда
Закон Архимеда. Погрузим тело произвольной формы (рис. 2.2.6) в жидкость. Тело находится в состоянии равновесия. Определим величину сил воздействующих на рассматриваемое тело. К рассматриваемому телу приложены поверхностные и массовые силы, а также моменты:
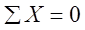 и
и 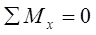
 и
и 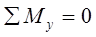 (2.3.21)
(2.3.21)
 и
и 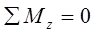
В случае состояния равновесия моменты сил уравновешены и исключаются из рассмотрения. Проекции рассматриваемых сил приведены на рис. 2.3.6.

Рис.2.3.6
Px, Py, Pz, Р|x, P|y, P|z–проекции сил соответственно на оси координат x,y,z.
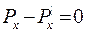
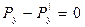 (2.3.22)
(2.3.22)

Учитывая, что данная система находится поле сил земного тяготения, массовая сила, действующая на погруженное тело, составит
G=γт×Wт, (2.3.23)
где Wт - объем погруженного тела, γт=ρg удельный вес погруженного тела.
В случае нахождения рассматриваемого тела в состоянии равновесия сумма поверхностных и массовых сил должна быть равна нулю.
 , (2.3.24)
, (2.3.24)
где G – сумма проекций массовых сил, 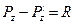 - сумма проекций поверхностных сил вдоль оси z.
- сумма проекций поверхностных сил вдоль оси z.
Подставляя в уравнение (2.3.24) составляющие получим
-γт×Wт+γв×ωz 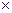 (hнhв)=0 (2.3.25)
(hнhв)=0 (2.3.25)
или
-γт×Wт+ γв×Wв=0 (2.3.26)
Из анализа уравнения (2.3.26) следует, что в случае равенства удельного веса тела и воды тело находится в состоянии покоя. При условии γв >γт тело должно всплыть, а при условии γв<γт тело опустится на дно емкости.
2.4 ОСНОВЫ ГИДРОДИНАМИКИ
2.4.1 Основные характеристики потока жидкости.
Поток жидкости. Под потоком жидкости подразумевается движение безразмерного множества отдельных частиц, которые движутся по своим траекториям. Как и в гидростатике, основной искомой величиной является величина гидростатического давления, а также значения скорости, расхода и т.п. при условии движения всех частиц жидкости.
Скорость течения потока. Под скорость движения потока жидкости подразумевается суммарное передвижение всех частиц потока в одном направлении. В связи представлением о скорости потока необходимо ввести ряд определений скорости.
Локальная скорость течения. Локальной скоростью движения жидкости является скорость движения безразмерно малой частицы жидкости.
Средней скоростью течения. Под средней скоростью движения потока жидкости подразумевается суммарное передвижение всех частиц потока в одном направлении, проходящее через площадку перпендикулярную векторам скорости. Локальная и средняя скорость движения потока жидкости связаны выражением:
 , (2.4.1)
, (2.4.1)
где  - локальная скорость;
- локальная скорость; 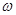 - площадь поперечного сечения движению потока.
- площадь поперечного сечения движению потока.
Установившийся (стационарный) поток движение жидкости. Установившимся потоком движение жидкости является поток, скорость в котором не зависит от времени рис 2.4.1.

Рис. 2.4.1.
Квазистационарный поток. Переменный, установившийся (квазистационарный) поток движения жидкости. Квазистационарным установившимся потоком движения жидкости является поток, скорость в котором меняется в установленном порядке от времени, рис 2.4.2.

Рис. 2.4.2
Неустановившийся поток. Неустановившийся (нестационарный) поток движение жидкости. Неустановившимся потоком движение жидкости является поток, скорость в котором зависит только от времени, рис 2.4.3

Рис. 2.4.3
Элементарная струйка. Понятие об элементарной струйке жидкости дает возможность рассматривать группу струек, движущихся совместно. Элементарна струйка (линяя тока) рис.2.4.4 может быть представлена как кривая, проходящая мгновенно совместно с такими же частицами, скорость которых направлены по касательной к этой кривой.
При этом установившееся движение можно представить как совокупность элементарных струек (линий тока), движущихся с равными скоростями частиц скользящими одна по другой. Линии тока в этом случае можно рассматривать как отдельные линии потока, к которым стремятся элементарные струйки при бесконечном уменьшении площадей их сечения. Такая совокупность движущихся струек образует поток жидкости.

Рис.2.4.4.
Траектория частицы не является линией тока. В частном случае (стационарный режим движения) линия тока совпадает с траекторией и описывается функцией траектории.
Расход жидкости. Произведение площади элементарной струйку потока жидкости  на величину локальной скорости движения U представляет некоторое количество жидкости. Это количество жидкости называется объемным элементарным расходом
на величину локальной скорости движения U представляет некоторое количество жидкости. Это количество жидкости называется объемным элементарным расходом
 . (2.4.2.)
. (2.4.2.)
Определение расхода всего потока жидкости затрудняется не знанием закона распределения скоростей по сечению.
В этом случае можно записать:
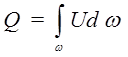 (2.4.3)
(2.4.3)
Предполагая толкование средней скорости потока как выражение:
 (2.4.4.)
(2.4.4.)
Исходя из выражения (2.4.4.) можно записать:
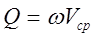 (2.4.5)
(2.4.5)
В отдельных случаях секундный расход жидкости измеряют в весовых единицах, в кгс/сек. Такой элементарный расход называют весовым:
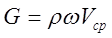 (2.4.6)
(2.4.6)
Смоченный периметр. Часть периметра поперечного сечения, образованного твердыми стенками, входящее в контакт с потоком жидкости, называется смоченным периметром. Следовательно, при напорном движении смоченный периметр меньше полного периметра поперечного сечения

Рис.2.4.5.
Гидравлический радиус. Гидравлический радиус представляют собой отношение площади поперечного сечения потока к его смоченному периметру Псм:
 , (2.4.7)
, (2.4.7)
где  - площадь поперечного сечения; Псм смоченный периметр.
- площадь поперечного сечения; Псм смоченный периметр.
Эквивалентный диаметр. Эквивалентный диаметр используется, как правило, в вентиляционной технике. Эквивалентный диаметр равен четырем гидравлическим радиусам.
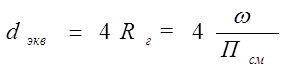 (2.4.8)
(2.4.8)
2.4.2 Уравнение неразрывности
Основным условием, которое должно соблюдаться при течении жидкости или газа, является непрерывность изменения параметров потока в зависимости от координат и времени. Это значит, что при течении жидкости должны быть соблюдены условия «сплошности». Жидкость или газ должны двигаться в соответствующих каналах как сплошная среда без разрывов. Сформулируем это условие. Отнесем поток жидкости к системе координат x, y, z (рис.2.2.11).

Рис. 2. 4.6.
В потоке выберем точку М с координатами x, y, z. Изолируем неподвижный объем в форме параллелепипеда со сторонами dx, dy и dz. Составляющие скорости течения жидкости в точке М равны: ux – вдоль оси x, uy – вдоль оси y, uz – вдоль оси z. Через площадку параллелепипеда dydz, в течение времени dt внутрь параллелепипеда втекает масса жидкости, равная ρuxdydzdt.
Из объема параллелепипеда в течение времени dt через площадку dydz, с координатами x + dx, y, z вытекает масса жидкости, равная
 (2.4.9)
(2.4.9)
Следовательно, при течении жидкости с составляющей скорости ux масса жидкости в объеме dxdydz изменяется на величину
 (2.4.10)
(2.4.10)
При прохождении жидкости через другие грани параллелепипеда масса жидкости в объеме dxdydz можно записать:
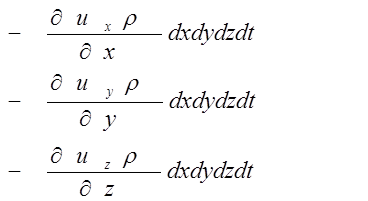 (2.4.11)
(2.4.11)
Суммарное изменение массы жидкости в объеме dxdydz равно:
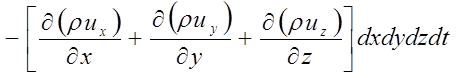 (2.4.12)
(2.4.12)
Изменение массы жидкости в объеме dxdydz может произойти только за счет изменения плотности ρ за период времени dt. В общем случае плотность жидкости или газа является функцией координат x, y, z и времени t, или ρ = f(x,y,z,t) Плотность жидкости в объеме, ограниченном dxdydz, может меняться как 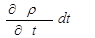 , а масса жидкости в элементарном объеме за период времени dt на
, а масса жидкости в элементарном объеме за период времени dt на 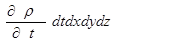 .
.
Для сохранения «сплошности» жидкости должно быть соблюдено условие:
 (2.4.13)
(2.4.13)
Уравнение (2.4.13) в гидромеханике называют уравнением неразрывности.
Если течение установившееся, то  , в этом случае уравнение «сплошности» можно представить следующим образом:
, в этом случае уравнение «сплошности» можно представить следующим образом:
 (2.4.14)
(2.4.14)
В том случае если жидкость несжимаемая ρ = const и тогда уравнение (2.4.14) примет вид:
 (2.4.15)
(2.4.15)
Рассмотрим уравнение «сплошности» (сохранения массы движущейся жидкости) для случая течения элементарной струйки при установившемся движении. Схема течение массы жидкости в элементарной струйке представлена на рис. 2.2.12. Пусть сечение 1-1 трубки тока имеет площадь dω1, и в этом сечении скорость жидкости u1, а ее плотность ρ1. Площадь сечения 2-2 трубки тока равна dω2, скорость сечения жидкости u2 и ее плотность ρ2. Скорости струйки направлены по касательной к стенкам трубки тока, поэтому через стенки обмен массой с окружающей жидкостью отсутствует. Через сечение 1-1 в трубку тока в единицу времени поступает масса жидкости, равная ρ1u1ω1. Через сечение 2-2 вытекает в единицу времени масса жидкости, равная ρ2u2ω2. В трубке тока масса жидкости, находящаяся между сечениями 1-1, 2-2 и 3-3 остается постоянной, следовательно, условие «сплошности» потока в трубке тока будет: 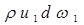 =
= 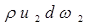 =
=  =const,т.е. вдоль трубки тока произведение ρuω остается постоянным.
=const,т.е. вдоль трубки тока произведение ρuω остается постоянным.
Рис.2.4.7. 
2.4.3 Основные дифференциальные уравнения движения невязкой жидкости

Рис. 2.4.8.
Рассмотрим элементарный объем в потоке жидкости рис.2.2.13. Запишем второй закон Ньютона для выделенной массы жидкости в проекции на оси xyz.
 (2.4.16)
(2.4.16)
Где Jx, Jy, Jz – проекции ускорения; m-масса выделенного объема; Rx, Ry, Rz, - сумма сил действующих на выделенный объем.
Проекцию ускорения можно выразить как
 (2.4.17)
(2.4.17)
Масса выделенного объема составляет:
 .(2.4.18)
.(2.4.18)
Проекции сил давления на соответствующие оси координат можно представить в виде:
 (2.4.19)
(2.4.19)
Массовые силы в проекциях на оси координат составят:
 (2.4.20)
(2.4.20)
Где X,Y,Z -проекции ускорений на соответствующие оси координат.
Подставляя рассмотренные составляющие в систему уравнений (46) (2.4.16) получим
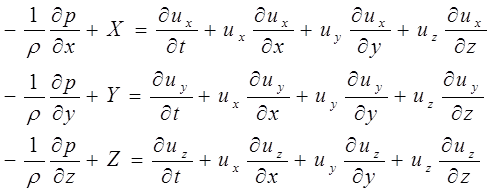 (2.4.21)
(2.4.21)
Данная система уравнений описывает движение идеальной жидкости.
В полученную систему уравнений входит пять неизвестных составляющих - ux, uy, uz, p и 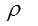 . Поэтому для решения указанной системы уравнений необходимо уравнение неразрывности и уравнение состояния (характеристическое уравнение)
. Поэтому для решения указанной системы уравнений необходимо уравнение неразрывности и уравнение состояния (характеристическое уравнение)
2.4.4 Уравнение движения вязкой жидкости
|
|
|
|
|
Дата добавления: 2015-06-26; Просмотров: 546; Нарушение авторских прав?; Мы поможем в написании вашей работы!