Введение 5 страница. Первые систематические опыты для выявления характера зависимости от Re и k/d были проведены в 1933 г

Рис 2.5.3

Первые систематические опыты для выявления характера зависимости от Re и k/d были проведены в 1933 г. И. Никурадзе в гладких латунных трубах и трубах с искусственной равномерно-зернистой шероховатостью из кварцевого песка.

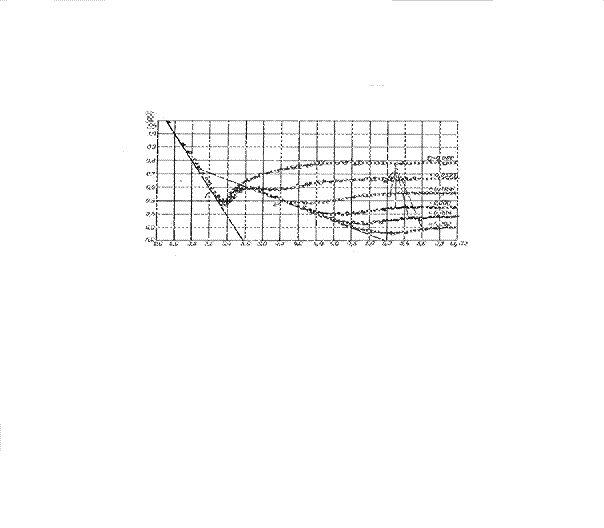
Рис.2.5.4

На рис. 2.5.4 показана зависимость величины гидравлического сопротивления трения 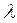от величины критерия Re. В данном случае ясно наблюдаются три области течения - первая область ламинарного течения, где потери связанные с трением, определяются не величиной относительной шероховатости, а только режимом течения. Вторая область – «гидравлически гладких труб» область течения жидкости в трубах в «переходном» режиме течения. Третья область – область развитого турбулентного течения. В данном случае гидравлический коэффициент трения практически не зависит от численных значений критерия Re, а основным фактором является относительная шероховатость, в данном случае от k/d=0,00197 до k/d=0,066.

2.5.3. Местные гидравлические сопротивления

Местные гидравлические сопротивления (потеря энергии в локальной области) появляются там, где происходит, например, изменение направления движения потока жидкости, ускорение или замедления его, присоединение или отсоединение потоков жидкости, в местах изменения скоростей и регулирования потока жидкости

Потери энергии связанные с преодолением потоком жидкости местных сопротивлений выражаются, как правило, в безразмерных единицах от скоростного напора потока. Эта величина определяется коэффициентом местного сопротивления - :

(2.5.3)

Основные группы местных сопротивлений можно обьеденить по следующим признакам:

- потери энергии, связанные с изменением поперечного сечения трубопровода (2.5.5 а. б. в.);

-потери энергии, связанные с изменением направления движения потока жидкости (2.5.6.а.б.);

-потери энергии, связанные с процессами присоединения или отделения потоков жидкости (2.5.7.а.б.в.г.д)

Внезапное расширение или сужение потока жидкости

Постепенное расширение или сужение потока жидкости

Устройства, регулиюрущие поток жидкости

Рис. 2.5.5

Изменение направления движения потока жидкости

Рис. 2.5.6.

Течение жидкости, связанное с процессами присоединения или отделения потоков жидкости.

Рис.2.5.7.

2.6. Гидравлический расчет трубопроводов

2.6.1 Простой и сложный трубопровод

При гидравлическом расчете трубопроводы подразделяют на простые и сложные. Под простым трубопроводом подразумевается трубопровод, состоящий из одной линии труб с постоянным расходом пути (рис. 2.6.1,а). Сложные трубопроводы состоят из сети труб. По пути движения жидкости

в сложных трубопроводах происходит изменение расхода. Подающий (собирающий) трубопровод подает жидкость сразу в ряд точек.

Сеть может быть разветвленной (разомкнутой или тупиковой рис. 2.6.1,б) или кольцевой (замкнутой рис. 2.6.1,в) и включать как транзитные участки трубопроводов (без раздачи жидкости по пути), так и распределительные трубопроводы.

Рис.2.6.1.

Рис.2.6.2

2.6.1. Простые трубопроводы

Рассмотрим простой трубопровод, состоящий из труб одного и того же диаметра или трубопровода с трубами различного диаметра (рис.2.6.2). Истечение проходит из резервуара в атмосферу. При течении по такому трубопроводу не происходит изменение расхода жидкости.

При истечении жидкости в атмосферу уравнение Бернулли, записанное для сечения 0-1 на поверхности воды в резервуаре и на выходе из трубы, имеет вид

(2.6.1)

Используя уравнение расхода производится расчет простых трубопроводов

При решении гидравлической системы решаются три задачи:

Первая задача. Требуется определить напор Н, необходимый для пропуска заданного расхода жидкости Q по заданному трубопроводу диаметром d и длиной l. Задача решается путем непосредственного использования формулы (2.6.1)с предварительным вычислением средней скорости V=4Q/(pd2). Тогда искомый напор можно определить из выражения:

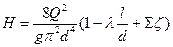(2.6.1)

Определение значений коэффициентов lи zв данной задаче не вызывает затруднений, так как число Рейнольдса заранее известно.

Вторая задача. Требуется определить пропускную способность (расход) трубопровода Q при условии, что известны напор Н, длина трубы и ее диаметр. Задача решается с помощью формулы (2.6.1), согласно которой:

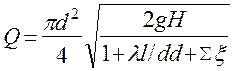(2.6.2)

Так как коэффициенты lи zявляются функциями числа Рейнольдса, которое связано с неизвестным и искомым здесь расходом Q, то решение находим методом последовательных приближений, полагая в первом приближении существование квадратичного закона сопротивления, при котором коэффициенты не зависят от числа Рейнольдса.

Третья задача. Требуется определить диаметр трубопровода d при заданном расходе Q, длине трубопровода l и напоре Н. Здесь также используем формулу (2), но встречаемся с затруднениями в вычислениях, так как не только неизвестно число Рейнольдса, но по отношению к искомому диаметру сы получаем уравнение высших степеней или даже (при определении lпо формуле Колбрука) трансцендентное уравнение. В связи с этим решаем задачу методом последовательных приближений, предполагая в первом приближении наличие квадратичного закона сопротивления, при котором коэффициент является функцией только диаметра (при заданной шероховатости стенок трубы).

Тогда уравнение приводится к виду:

(2.6.3)

Рис.2.6.3

Задаваясь рядом значений диаметра d-1, d -2,...d-n и вычисляя по последней формуле соответственно ряд значений расхода Q-1, Q-2,...Q-n, строим график Q=f(d) из которого определяем диаметр, отвечающий заданному расходу.

2.6.2 Сложные трубопроводы.

Сложные трубопроводы состоят из сети труб. По пути движения жидкости в сложных трубопроводах происходит изменение расхода. Подающий (собирающий) трубопровод подает жидкость сразу в ряд точек. Сеть может быть разветвленной (разомкнутой или тупиковой (2.6.1,б) или кольцевой (замкнутой рис. 2.6.1,в) и включать как транзитные участки трубопроводов (без раздачи жидкости по пути), так и распределительные участки трубопроводов.

2.6.3. Расчет сложного тупикового трубопровода

Рис. 2.6.3

Расчет сложного трубопровода (рис.2.6.3)проводится по следующему алгоритму:

- определяется самое протяженное и нагруженное направление движения жидкости по сети (магистральное направление, участки 1-2-3-4 рис 2.6.3.);

- по магистральному направлению определяются расчетные участки. Границей расчетного участка является точка изменения расхода жидкости.

- на расчетных участках определяется расход жидкости - Q (м\ч), его длина – l (м);

- задается скорость движения жидкости на расчетных участках v (м\с)

- используя уравнение расхода - определяется площадь поперечного сечения канала - (м)

- зная поперечную площадь канала, определяем диаметр трубопровода

; ()

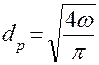- по расчетному диаметру подбирается действительный диаметр трубопровода 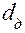, соответствующий стандартному сортаменту труб;

- по значению действительного диаметра трубопровода уточняется скорость движения жидкости

;

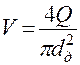- зная величину действительной скорости и диаметр трубопровод на участке определяется режим течения, используя критерий Рейнольдса

;

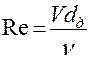- по численной величине критерия Рейнольса определяем значение коэффициента гидравлического сопротивления трения , например, по формуле А.Д. Альтшуля;

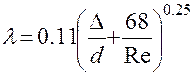
- определяем потери давления на трение по расчетным участкам используя известную формулу Дарси-Вейсбаха

;

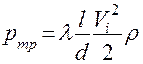- определяем значения величин местных сопротивлений - на расчетных участках (с учетом режима течения по численному значению критерия Re) и находим потери давления в местных сопротивлениях:

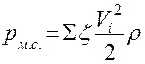
- находим общие потери давления на расчетных участках- ;

- определяем суммарную потерю давления по магистральному направлению

;

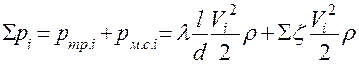- находим потери давления по ответвлениям (участки 5-6-7-8-9) и увязываем потери давления по указанным участкам с давлением на участке магистрального трубопровода;

- по полученным значениям потери давления расходу жидкости - подбирается гидравлическая машина.

2.6.3. Расчет сложного кольцевого трубопровода

Расчет сложного трубопровода (рис.) представляет собой достаточно сложную гидравлическую задачу. Однако, решение данной задачи упрощается если представится возможным выделить точку «схода» (см.рис). Под точкой схода подразумевается участок трубопровода, на котором «гипотетически» расход жидкости нулевой.

В этом случае алгоритм расчета сводится к следующим шагам:

- выбирается точка «схода» по признакам удаленности и загруженности магистральных направлений движения жидкости;

- полученные трубопроводы рассчитываются по схеме приведенной в разделе 2.6.3 как «тупиковые»;

- полученная невязка «левого» и «правого» контура устраняется установкой дополнительного запорно-регулирующего оборудования с байпасной линией.

СПИСОК ЛИТЕРАТУРЫ

1.Н.В. Луканин и др. Теплотехника. М., В.Ш. 2002.

2.Альтшуль А.Д. и др. Гидравлика и аэродинамика. М.: Стройиздат, 1987.

3. А.П. Давыдов. Методические указания по проведению лабораторных работ по гидравлике КГАСУ, 2011.

4. А.П. Давыдов. Примеры решения задач по гидравлике. УП. Казань. КГАСУ. 2008.

Дата добавления: 2015-06-26