Лабораторная работа 1.01

Прямые измерения физических величин

Цель работы: освоить методику использования измерительного прибора, многократно измерить физическую величину, рассчитать погрешности измерений.

Принадлежности: по указанию преподавателя.

ТЕОРИЯ

Физика не может существовать без эксперимента. А современный эксперимент предполагает в конечном итоге получение определенных числовых значений какой-либо физической величины, т.е. получение результатов измерений.

1. Измерения.

Измерение –это нахождениечисловогозначения физической величины опытным путем с помощью специальных технических средств.

Измерения делятся на прямые, косвенные и совместные.

Прямыми называются измерения, при которых значения физической величины измеряется непосредственно с помощью прибора. Примеры: измерение длины линейкой, измерение напряжения вольтметром, времени – секундомером, частоты - частотомером и т.д.

Косвенными называются измерения, при которых для нахождения физической величины в данных условиях эксперимента необходимо использовать связь в виде формулы с другими, непосредственно измеряемыми величинами. Примеры: нахождение объема тела по его линейным размерам; расчет сопротивления проводника по показаниям вольтметра и амперметра.

Совместными называются одновременные измерения двух или более неодноименных величин при изменяющихся условиях опыта. Пример: измерение температуры тела с течением времени, измерение силы тока и напряжения в электрической цепи.

2. Погрешности.

При измерении какой-либо физической величины экспериментатор получает результат измерения. Однако нельзя утверждать, что он получил истинное значение измеряемой величины. Можно утверждать только то, что результат измерения близок к истинному значению. Иначе говоря, результаты измерений всегда приближенны, то есть содержат некоторую погрешность (т.е. отклонение результата измерения физической величины от ее истинного значения).

Погрешность измерения (абсолютную погрешность) можно определить как разность между измеренным значением физической величины и ее истинным значением 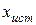, т.е.

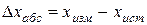, (1)

где 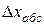- абсолютная погрешность измерения.

Но абсолютная погрешность не полностью характеризует качество измерений. Например, если при измерении массы тела погрешность 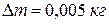, это много или мало? При взвешивании стального прутка мало, а при составлении химических реактивов может оказаться много. Поэтому для полной характеристики измерений, наряду с абсолютной вводится относительная погрешность – отношение абсолютной погрешности к истинному значению измеряемой величины

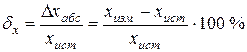. (2)

Относительная погрешность обычно выражается в процентах. Она показывает, какую часть измеряемой величины составляет средняя абсолютная погрешность

Выполнив серию наблюдений, можно ввести абсолютную погрешность для каждого из результатов наблюдений по формуле

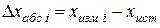, (3)

где 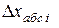- абсолютная погрешность i -го наблюдения.

3. Классификация погрешностей.

Погрешности измерений по характеру можно разделить на три категории.

Систематической называется такая погрешность измерения, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же физической величины. Такие погрешности появляются вследствие неточности измерительных приборов, различных упрощающих условий в методе исследования и т.д. Уменьшить влияние систематической ошибки можно используя более точные приборы, совершенствуя метод исследования.

Случайной называется погрешность, которая изменяется при измерениях случайным образом при повторных измерениях. Случайные погрешности можно уменьшить путем многократных измерений, а величину погрешности вычислить методами математической статистики.

Грубая погрешность (или промах) – это погрешность, существенно превышающая предполагаемую погрешность в данных условиях измерения. Эта категория погрешностей встречается весьма редко, и ее появление связано либо с неисправностью приборов, либо с несовершенством методики эксперимента. Если такая погрешность установлена, то соответствующий результат измерения исключается из дальнейшей обработки.

Для вычисления погрешностей измерений экспериментатору необходимо овладеть некоторыми методами математической статистики.

4. Гистограммы.

Случайные погрешности результатов эксперимента можно рассматривать как разновидность случайных величин (событий), т.е. переменных величин, значения которых зависят от случая. Случайные величины могут принимать любые действительные значения.

Всевозможные свойства большого количества случайных величин изучаются теорией вероятностей, основным понятием которой является вероятность – числовая характеристика возможности появления некоторого определенного события в цепи событий, которые могут повторяться неограниченное число раз.

Допустим, что при выполнении n измерений физической величины х получен некоторый набор чисел

.

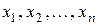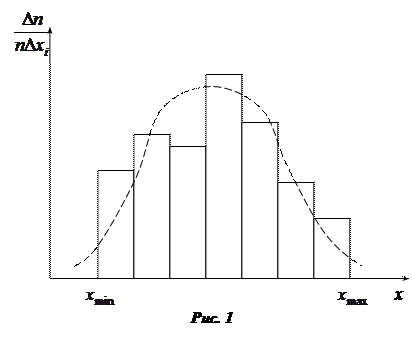
Результаты серии измерений можно наглядно представить, построив диаграмму, которая показывает, как часто получаются те или иные значения. Такая диаграмма называется гистограммой. Чтобы построить гистограмму, разбиваем весь диапазон на равные интервалы 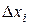. Для этого из всех измерений находим 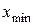и 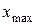. Определяем ширину интервала по формуле 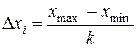(k – любое целое число от 5 до 10) и подсчитываем, сколько раз измеренная величина попадает в каждый интервал 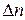. При построении гистограммы в прямоугольных координатах по оси абсцисс откладывают границы интервалов, а по оси ординат – отношение 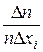, где п – общее число измерений (см. рис. 1). Площадь каждого прямоугольника будет численно равна вероятности данного события. Площадь всех прямоугольников

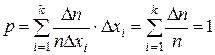. (4)

Таким образом, сумма вероятностей всех возможных событий равна единице. Величина 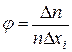называется плотностью вероятности.

5. Характеристики распределения случайных величин.

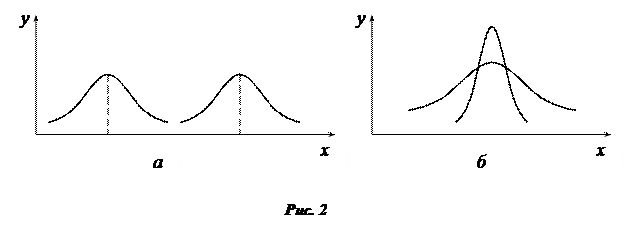
Существуют две основные характеристики, по которым можно определять сходство или различие распределений: расположение центра группирования, вокруг которого сосредоточено все распределение, и степень рассеяния данных измерения от центра группирования.

На рис. 2 графически представлены различные распределения случайных величин. По оси 0х отложены значения случайных величин, по оси 0у – частоты их появления. На рис. 2, а представлены два распределения, отличающихся расположением центра группирования, а на рис. 2, б – степенью рассеяния.

Основной характеристикой положения центра группирования является среднее арифметическое , которое рассчитывается по формуле

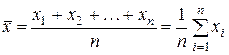. (5)

Для описания рассеяния существует несколько характеристик, но лучше всего характеризуют рассеяние измеренной величины дисперсия и среднеквадратичное отклонение.

Дисперсия определяется по формуле

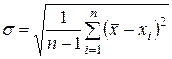. (6)

Среднеквадратичное отклонение 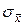определяется как

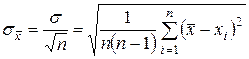. (7)

6. Нормальное распределение случайной величины.

При бесконечно большом числе измерений и уменьшении размеров интервалов группирования гистограмма переходит в непрерывную кривую, которая аналитически наиболее часто описывается формулой Гаусса, получившей название нормального закона распределения случайных величин. Основная формула нормального распределения записывается так:

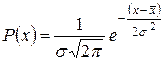, (8)

где 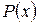– вероятность появления случайной величины, численное значе-

ние которой равно х;

– среднеарифметическое ее значение.

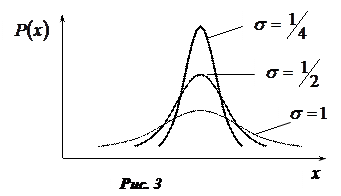Из формулы (8) видно, что нормальное распределение определяется двумя параметрами: и 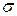. Кривые, соответствующие формуле (8) (кривые Гаусса) для разных 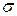, приведены на рис. 3. То есть зная параметр 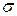для данного метода измерения, можно количественно характе-ризовать степень рассеяния результатов измерений.

7. Доверительная вероятность и доверительный интервал.

Доверительной вероятностью (надежностью) результата серии измерений называется вероятность 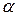того, что истинное значение измеряемой величины попадет в доверительный интервал .

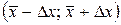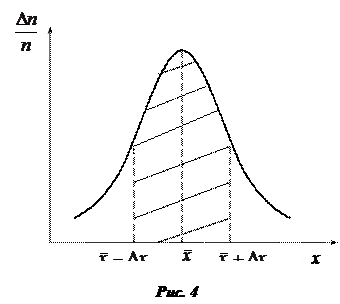Величина доверительной вероятности на рис. 4 определяется площадью заштрихованной области. Чем шире доверительный интервал, тем с большей вероятностью искомая величина попадет в него.

При малом числе повторных измерений п полуширина интервала вычисляется по формуле

,

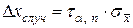где 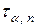– коэффициент Стъюдента, который зависит от доверительной вероятности и от числа измерений довольно сложным образом. Методы математической статистики позволяет вычислить коэффициенты 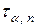для любых 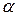и п. Результаты таких вычислений сведены в таблицу (см. ниже). Оценку погрешности в обычных экспериментах находят при доверительной вероятности 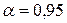, в ответственных случаях – при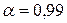

8. Расчет погрешностей для прямых измерений.

Пусть в результате серии прямых независимых измерений физической величины х, проведенных при одних и тех же условиях, получили п значений величины:

.

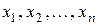За оценку истинного значения принимают среднее арифметическое

Оценка погрешности среднего арифметического имеет случайную и систематическую составляющие.

а) Случайная погрешность.

Чтобы определить случайную погрешность, следует

1) вычислить среднее значение измеряемой величины по формуле

;

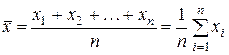2) Определить среднеквадратичное отклонение среднего арифметического

;

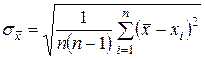3) По заданной преподавателем доверительной вероятности 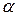и числу измерений п найти коэффициент Стъюдента по таблице;

4) Определить случайную погрешность по формуле

.

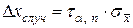б) Систематическая погрешность.

Систематические погрешности можно условно разделить на три группы:

1) систематические погрешности, природа и величина которых известна;

2) систематические погрешности, природа которых известна, а величина – нет;

3) систематические погрешности, о существовании которых мы не подозреваем.

Погрешности первой группы обычно исключаются введением поправок. Обнаружение и устранение погрешностей третьей группы – это вопрос квалификации и интуиции экспериментатора.

К систематической погрешности второй группы относится приборная погрешность. Для ее учета вводится предел допускаемой погрешности 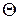- максимально возможная погрешность прибора данного типа.

Для электроизмерительных стрелочных приборов указывается класс точности. Число, обозначающее класс точности (например: 0,005; 0,1; …, 0,4) представляет максимальную погрешность прибора, выраженную в процентах от конечного значения шкалы. Например: на шкале миллиамперметра с диапазоном показаний от 0 до 100 мА стоит цифра 4,00. Эта цифра показывает, что класс точности миллиамперметра 4 %, а предел его допускаемой погрешности равен 4 % конечного значения шкалы, т.е. составляет 4 мА. Если измерить этим миллиамперметром ток 10 мА, то погрешность окажется равной 40 %.

Если класс точности прибора не указан, то за величину погрешности принимают 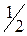цены его минимального деления. Такое же правило существует для оценки погрешности линеек и других приборов с нанесенными шкалами. Например: на штангенциркуле нанесена метка с цифрами 0,05 мм. Значит погрешность прибора .

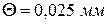Погрешность цифрового прибора оценивается по формуле погрешностей, приведенной в паспорте прибора. Для однотипных приборов эти формулы часто совпадают. Если измерение производится цифровым прибором не на самых чувствительных диапазонах, то за погрешность можно принять единицу младшего разряда.

в) Сравнение случайных и приборных погрешностей. Суммарная

Дата добавления: 2015-06-26