Определение ошибок выборки

После выбора способа выборочного наблюдения, регистрации признака, осуществляют расчет обобщающих характеристик. Определяют выборочную среднюю или выборочную долю 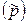единиц, обладающих данным признаком в общей их численности.

Разность (расхождение) между показателями выборочной и генеральной совокупности называются ошибками выборки. Ошибки выборки подразделяются на ошибки регистрации и ошибки репрезентативности.

Ошибки регистрации возникают из-за неправильных или неточных сведений (невнимательность, пропуск, описки...). Ошибки регистрации могут быть систематическими (округление цифр, тяготение к цифрам с нулями, десятками, сотнями...) и случайными.

Ошибки репрезентативности также могут быть систематическими (в результате тенденциозного, неправильного отбора) и случайными (недостаточно точно воспроизводят всю совокупность).

Разность между показателями выборочной и генеральной совокупности и будет случайной ошибкой репрезентативности.

;

.

Выборочная средняя и выборочная доля являются случайными величинами, ошибки выборки также случайны и могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок.

Среднюю ошибку выборки определяют по формуле:

,

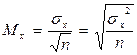- как частное от деления среднего квадратического отклонения на квадратный корень из численности выборки или квадратный корень из дисперсии признака,

где, 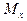- средняя ошибка выборки;

- численность единиц выборочной совокупности;

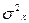- дисперсия варьирующего признака;

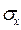- среднее квадратическое отклонение.

Для доли средняя ошибка выборки определяется по формуле:

В этих формулах и 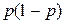являются характеристиками генеральной совокупности, которые при выборочном наблюдении неизвестны. На практике их заменяют аналогичными характеристиками выборочной совокупности на основании закона больших чисел, по которому выборочная совокупность при достаточно большом объеме достаточно точно воспроизводит характеристики генеральной совокупности. Следовательно, средние ошибки выборки можно представить следующим образом:

а) при повторном отборе -

для средней: ; для доли: .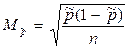

При бесповторном отборе подкоренное выражение умножается на величину, которая всегда меньше единицы, поэтому величина средней ошибки выборки при бесповторном отборе оказывается меньше, чем при повторном. В тех случаях, когда доля выборки незначительна и множитель близок к 1, поправкой можно пренебречь;

б) при бесповторном отборе (единицы совокупности, попавшие в выборку в дальнейшем отборе не участвуют, что дает более точные результаты):

· при определении средней: ;

· при определении доли: .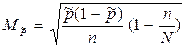

Рассчитывают ошибки репрезентативности. Случайные ошибки репрезентативности могут быть доведены до незначительных размеров. Их величину и пределы можно определить с достаточной точностью на основании закона больших чисел с использованием теории вероятности.

Возможные пределы отклонения выборочной доли и выборочной средней от доли и средней генеральной совокупности носят названия предельных ошибок выборки .

В зависимости от способа отбора (повторного - способ возвращенного шара и бесповторного - способ невозвращенного шара) предельные ошибки выборки определяются следующим образом:

а) при повторном отборе -

· при определении доли:

· при определении средней:

,

б) При бесповторном отборе (единицы совокупности, попавшие в выборку в дальнейшем отборе не участвуют, что дает более точные результаты):

· при определении доли: ;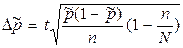

· при определении средней: .

где t - коэффициент доверия, зависит от вероятности, с которой можно гарантировать, что предельная ошибка не превысит t - кратную среднюю ошибку.

Если доля выборки незначительна (до 5%), то выражение 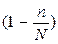можно не учитывать;

С увеличением t возрастает вероятность нашего утверждения, но вместе с тем увеличивается величина ошибки, т. е. чем больше пределы, в которых допускается возможная ошибка, тем с большей вероятностью можно установить ее величину.

Величина коэффициента t зависит от вероятности, с которой гарантируется точность расчетов; Р- доверительная вероятность: т.е. в 683 случаях из 1000; t - коэффициент доверия (см.табл.)

Значения t приводятся в специальных таблицах вероятностей:

p - доверительная вероятность t - коэффициент доверия

0,683 1,0

0,866 1,5

0,927 1,8

0,943 1,9

0,954 2,0

0,979 2,31

0,988 2,5

0,997 3,0

0,999 3,5

Чаще применяют t = 1, 2, 3. Так, если t = 2, то с вероятностью 0,954 можно утверждать, что разность между выборочными и генеральными показателями не превысит одной средней ошибки (t - кратную среднюю ошибку)?

После исчисления предельных ошибок выборки находят границы искомых показателей в генеральной совокупности. Определяется так:

· для средней ошибки:

· для доли: .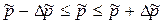

Кроме средней ошибки при решении практических задач пользуются предельной ошибкой выборки. Предельная ошибка выборки связана с гарантирующем ее уровнем вероятности.

Приведенные формулы ошибки выборки характеризуют среднюю величину отклонений сводных характеристик генеральной совокупности от соответствующих характеристик выборочной совокупности. Однако то, что генеральная средняя или генеральная доля не выйдет за определенные пределы можно утверждать не с абсолютной точностью, а лишь с определенной степенью вероятности, на величину которой указывает t - коэффициент доверия.

Следовательно, с определенной вероятностью можно утверждать, что отклонение выборочных характеристик от генеральной не превышает некоторой величины, которая называется предельной ошибкой выборки ().

Формулы для расчета объема выборки:

а) при повторном отборе:

· для средней: 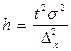; для доли: ;

б) при бесповторном отборе:

· для средней: 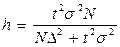; для доли: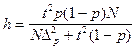

Дата добавления: 2015-06-26