Основные определения, обозначения и формулы

В примерах 1, 2, 3 рассматривались конечные множества и их подмножества, в которых элементы расположены в определенном порядке.

Размещения (от франц. arrangement — размещение, приведение в порядок). Пусть дано множество, состоящее из n элементов. Размещением из n элементов по k (0 £ k £ n) элементов называется упорядоченное подмножество, содержащее k различных элементов данного множества. Все эти подмножества отличаются друг от друга или составом элементов, или порядком их распределения.

Число всех возможных размещений обозначают символом 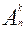(читают: число размещений из n элементов по k элементов) и вычисляют по формуле: 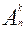=n´(n–1)´…´(n–k+1), т.к. первый элемент подмножества можно взять n различными способами, второй — (n–1) способом, третий — (n–2) способами, четвертый — (n–3) способами и т.д. (пример 2).

Пример 4. В соревнованиях принимают участие 9 танцевальных пар, сколькими способами могут распределиться три первых места.

Решение. Пронумеруем все танцевальные пары. Получим конечное множество из 9 элементов (каждая пара элемент множества). Надо найти число всех подмножеств этого множества, состоящих из трех элементов, отличающихся составом (номерами пар) или порядком их размещения, то есть подмножества {№5, №4, №6} и {№4, №5, №6} являются разными. Следовательно, надо найти все размещения из 9 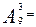элементов по 3 элемента, то есть 9´8´7=504.

Перестановки (от французского permutation — перестановка, перемещение). Перестановкой из n элементов называется размещение из n элементов по n элементов. Следовательно, различные перестановки отличаются друг от друга только порядком элементов (пример 1).

Число всех возможных перестановок из n элементов обозначают P_n и вычисляют по формуле P_n= =n´(n–1)´… ´2´1, то есть число различных перестановок из n элементов равно произведению всех последовательных натуральных чисел, начиная от n и до 1 включительно.

Pn=n!

Знак! «факториал» — это произведение целых чисел от 1 до n.

Например, 1!=1

2!=1´2=2

3!=1´2´3=6

4!=1´2´3´4=24 и т.д.

По определению 0!=1

Пример 5. Сколькими способами можно расставить 6 различных книг на одной полке?

Решение. Р₆=6!=6´5´4´3´2´1=720. Первую книгу можно выбрать шестью способами, вторую — пятью способами и т.д., последнюю — одним способом.

Пример 6. Сколько различных пятизначных чисел можно написать с помощью пяти цифр 1, 2, 3, 4, 5 так, чтобы каждая цифра повторялась только один раз?

Решение. Р₅=5!

Сочетания (от французского combinaison — сочетание, комбинация). Пусть дано множество, состоящее из n элементов. Сочетанием из n элементов по k (0 £ k £ n) элементов называется любое подмножество, содержащее k различных элементов данного множества. Различными сочетаниями считаются только те, которые отличаются составом элементов (пример 3).

Число всех возможных сочетаний обозначают символом (читают: число сочетаний из n элементов по k элементов) и вычисляют по формуле:

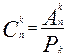, следовательно, ´P_k

Пример 7. Отряд вожатых состоит из 15 человек, для работы в одной смене летнего лагеря необходимо выбрать 6 вожатых. Сколькими способами это можно сделать?

Решение. Так как порядок выбранных восьми человек не имеет значения, то в данном случае надо найти число сочетаний из 15 элементов по 6 элементов, то есть

Дата добавления: 2015-06-26