
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Правила комбинаторики
|
|
|
|
Правило суммы. Если некоторый выбор из совокупности можно сделать n различными способами, а другой выбор — m различными способами (отличными от предыдущих), то общее число способов, которыми можно осуществить какой-нибудь из этих выборов, равен сумме n+m.
Пример 8. Сколько всего различных двузначных и трехзначных чисел можно записать цифрами 7, 3, 1, 2?
Решение. Необходимо найти количество двузначных чисел, затем количество трехзначных чисел и сложить полученные результаты. Так как порядок расположения цифр в числе имеет значение, то есть числа 37 и 73 — это разные числа, то количество двузначных чисел равно числу размещений 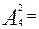 4´3=12, а количество трехзначных чисел равно
4´3=12, а количество трехзначных чисел равно  4´3´2=24, пользуясь правилом суммы, можно найти общее число различных двузначных и трехзначных чисел 12+24=36.
4´3´2=24, пользуясь правилом суммы, можно найти общее число различных двузначных и трехзначных чисел 12+24=36.
Правило произведения. Если некоторый выбор из совокупности можно сделать n различными способами, а для каждого из этих способов некоторый второй выбор можно сделать m различными способами, тогда число способов для проведения последовательно двух этих выборов равно произведению n´m.
Пример 9. Клавиатура пианино состоит из 88 клавиш (нот). Сколько различных музыкальных фраз можно составить из 6 нот, если не допускать в одной фразе повторение одних и тех же нот.
Решение. В качестве первой ноты для музыкальной фразы можно взять любую из 88 нот, то есть для первой ноты имеем 88 возможностей. Так как повторения не допускаются, то для второй ноты имеем лишь 87 возможностей, для третьей ноты останется лишь 86 возможностей, рассуждая аналогично, получим, что число различных музыкальных фраз из 6 нот без повторения равно произведению 88´87´86´85´84´83=390 190 489 920.
|
|
|
|
|
Дата добавления: 2015-06-26; Просмотров: 693; Нарушение авторских прав?; Мы поможем в написании вашей работы!