
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Точки, в которых нарушается конформное отображение
|
|
|
|
Будем изучать отображение 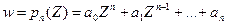 (
(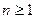 ) (1). Очевидно, производная
) (1). Очевидно, производная 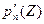 принимает нулевое значение лишь в точках
принимает нулевое значение лишь в точках  . Поэтому в этих точках может нарушаться конформность отображения. В остальных точках отображение
. Поэтому в этих точках может нарушаться конформность отображения. В остальных точках отображение 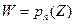 будет конформным, так как
будет конформным, так как 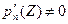 .
.
В случае n = 1 мы получаем точку 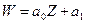 (
(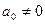 ). Как мы знаем, это отображение будет конформным во всей расширенной плоскости. Поэтому мы будем изучать случай, когда
). Как мы знаем, это отображение будет конформным во всей расширенной плоскости. Поэтому мы будем изучать случай, когда 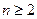 . Покажем, что при
. Покажем, что при 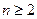 нарушает конформность отображение (1) в любой точке
нарушает конформность отображение (1) в любой точке 
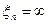 . Как мы знаем, в этих точках производная
. Как мы знаем, в этих точках производная 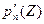 обращается в нуль и в последней в ∞. Обозначим через Z0 какую-нибудь из точек
обращается в нуль и в последней в ∞. Обозначим через Z0 какую-нибудь из точек  и покажем, что в ней нарушает конформность отображения (1).
и покажем, что в ней нарушает конформность отображения (1).
Так как Z0 является кратным корнем уравнения 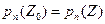 , то имеет место представление
, то имеет место представление 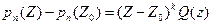 , где
, где 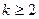 , а Q(Z) – это многочлен степени n – k, такой, что
, а Q(Z) – это многочлен степени n – k, такой, что 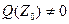 . Возьмем в плоскости (Z) кривую
. Возьмем в плоскости (Z) кривую 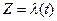 ,
,  , проходящую через точку
, проходящую через точку 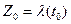 . Мы будем считать, что
. Мы будем считать, что 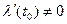 , то есть кривая имеет в точке Z0 касательную. Отображение
, то есть кривая имеет в точке Z0 касательную. Отображение 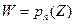 переведет эту кривую в
переведет эту кривую в 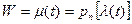 ,
,  , проходящую через точку
, проходящую через точку 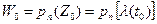 . Непосредственно не видно, что кривая
. Непосредственно не видно, что кривая 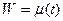 имеет в точке
имеет в точке 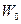 касательную, так как производная
касательную, так как производная 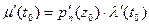 .
.
Покажем, что кривая 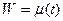 имеет в точке
имеет в точке 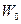 касательную. С этой целью возьмем
касательную. С этой целью возьмем  и проведем через точки
и проведем через точки 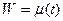 и
и 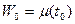 секущую. Очевидно, угол, который составляет эта секущая с осью и будет равен
секущую. Очевидно, угол, который составляет эта секущая с осью и будет равен 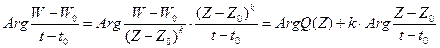 .
.
Произведя здесь предельный переход при 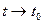 , получим, что
, получим, что  (2), следовательно, касательная к кривой
(2), следовательно, касательная к кривой 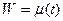 в точке
в точке 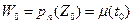 существует и составляет с осью угол, равный величине (2). Выпустим из точки Z0 какие-нибудь две кривые
существует и составляет с осью угол, равный величине (2). Выпустим из точки Z0 какие-нибудь две кривые 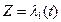 и
и 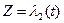 ,
, 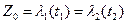 , которые образуют между собой угол в точке Z0, равный
, которые образуют между собой угол в точке Z0, равный 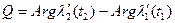 . Отображение
. Отображение 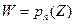 переведет кривые
переведет кривые 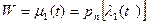 ,
, 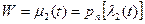 в проходящие через точку
в проходящие через точку 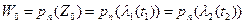 . Эти кривые составляют между собой угол, равный
. Эти кривые составляют между собой угол, равный  , то есть при отображении
, то есть при отображении 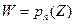 в точке Z0 угол между кривыми увеличивается в
в точке Z0 угол между кривыми увеличивается в 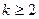 раз. То есть в этой точке нарушается конформность отображения.
раз. То есть в этой точке нарушается конформность отображения.
Аналогичным образом показывается, что нарушается конформность отображения 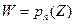 (
(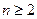 ), и в точке
), и в точке 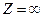 угол между кривыми увеличивается в n раз, при этом надо пользоваться отображением
угол между кривыми увеличивается в n раз, при этом надо пользоваться отображением 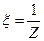 .
.
Отображение 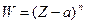 (1).
(1).
Рассмотрим отображение (1), где a – фиксированное комплексное число, а n – натуральное число. При n = 1 мы получаем отображение 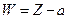 , оно конформно в расширенной плоскости. Будем считать, что
, оно конформно в расширенной плоскости. Будем считать, что 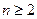 . Очевидно, что
. Очевидно, что 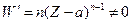 во всех точках
во всех точках 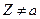 . Следовательно, это отображение является конформным во всех точках Z комплексной плоскости отличных от a.
. Следовательно, это отображение является конформным во всех точках Z комплексной плоскости отличных от a.
По доказанному, конформность нарушается лишь в двух точках 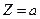 и в точке
и в точке 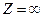 . Углы между кривыми в этих точках увеличиваются в n раз. Изучим более подробно отображение (1). Очевидно, любая точка
. Углы между кривыми в этих точках увеличиваются в n раз. Изучим более подробно отображение (1). Очевидно, любая точка 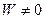 и ∞ имеет в плоскости (W) ровно n прообразов
и ∞ имеет в плоскости (W) ровно n прообразов 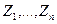 , которые определяются формулой
, которые определяются формулой
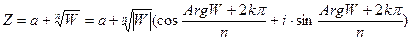 , (k=0, 1,…, n-1) (2).
, (k=0, 1,…, n-1) (2).
Из формулы (2) непосредственно видно, что все эти прообразы располагаются в вершинах правильного n -угольника, вписанного в окружность радиуса 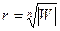 с центром в точке a.
с центром в точке a.

Точки же 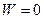 и
и  имеют в плоскости (Z) лишь по одному прообразу. Соответственно
имеют в плоскости (Z) лишь по одному прообразу. Соответственно 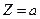 и
и 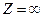 . Выясним, как изменяются углы между кривыми в точках
. Выясним, как изменяются углы между кривыми в точках 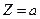 и
и 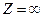 . Из равенства (1) непосредственно следует, что
. Из равенства (1) непосредственно следует, что
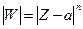 (3)
(3)
 (4).
(4).
Эти формулы позволят увидеть, во что отображают функции (1) окружность с центром в точке a и лучи, исходящие из точки a в окружность и луч, исходящий из нуля.
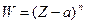 ,
, 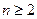 (1)
(1)
Из (1) 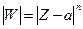 (3)
(3)
 (4).
(4).
Из равенств (3) и (4) непосредственно следует, что функция (1) отображает окружность 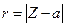 радиусом r c центром в точке a на окружность
радиусом r c центром в точке a на окружность 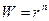 радиуса
радиуса  с центром в точке ноль.
с центром в точке ноль.
В самом деле: в силу равенства (3) окружность 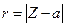 отображается в окружность
отображается в окружность 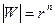 , из равенства (4) вытекает, что когда точка Z описывает рассматриваемую окружность в положительном направлении один раз, соответствующая точка W описывает окружность в положительном направлении n раз.
, из равенства (4) вытекает, что когда точка Z описывает рассматриваемую окружность в положительном направлении один раз, соответствующая точка W описывает окружность в положительном направлении n раз.

Из тех же равенств (3) и (4) вытекает, что функция (1) отображает луч 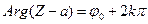 (5) на луч
(5) на луч 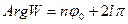 (6).
(6).

В самом деле, из равенства (4) непосредственно следует, что луч (5) отображается в луч (6). Из формулы (3) следует, что когда точка Z, выходя из точки a и удаляясь в бесконечность, полностью описывает луч (6) (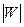 непрерывно меняется от
непрерывно меняется от 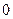 до ∞).
до ∞).
Рассмотрим теперь в плоскости (Z) угол раствора 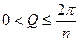 с вершиной в точке a, ограниченный лучами
с вершиной в точке a, ограниченный лучами 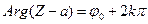 (7) и
(7) и 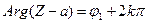 (8), где
(8), где 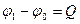 .
.

Нетрудно видеть, что функция 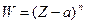 отобразит этот угол на угол раствора Q с вершиной в нуле, ограниченного лучами
отобразит этот угол на угол раствора Q с вершиной в нуле, ограниченного лучами 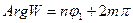 (9) и
(9) и 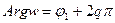 (10). Обозначим внутренность угла плоскости (Z) через d, а плоскости (W) – через q. Нетрудно видеть, что функция
(10). Обозначим внутренность угла плоскости (Z) через d, а плоскости (W) – через q. Нетрудно видеть, что функция 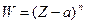 отображает взаимно однозначно и конформно область d на область q. То, что это отображение конформно во всех точках d следует из того, что производная
отображает взаимно однозначно и конформно область d на область q. То, что это отображение конформно во всех точках d следует из того, что производная 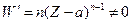 (где точка a исключается, так как не принадлежит внутренности).
(где точка a исключается, так как не принадлежит внутренности).
Нам остается доказать, что это отображение является взаимно однозначным. Мы знаем, что d отображается на q. Очевидно, отображение (1) является однозначным, поэтому нам достаточно доказать, что любая точка 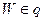 имеет в d и при том только один прообраз.
имеет в d и при том только один прообраз.
То, что этот, хотя бы один прообраз существует, следует из того, что d отображается на q. Нам остается доказать единственность этого прообраза. Как мы знаем, прообразы точки w располагаются в вершинах правильного n -угольника с центром в точке a. Поэтому в d могут попасть несколько прообразов лишь в том случае, когда раствор угла будет больше, чем 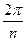 . У нас же раствор угла не превышает
. У нас же раствор угла не превышает 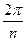 . Поэтому W имеет в d только один прообраз. Мы пришли к теореме.
. Поэтому W имеет в d только один прообраз. Мы пришли к теореме.
|
|
|
|
|
Дата добавления: 2015-06-26; Просмотров: 490; Нарушение авторских прав?; Мы поможем в написании вашей работы!