Групповое свойство дробно-линейной функции

Свойства дробно-линейной функции

Лекция № 13

Пример.

Теорема.

Функция 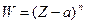взаимно однозначно и конформно отображает внутренность угла раствора 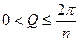с вершиной a, ограниченного лучами на внутренность угла плоскости (W) с раствором 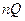с вершиной в нуле, ограниченного соответствующими лучами.

Отобразить взаимно однозначно и конформно внутренность угла, ограниченного лучам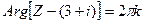и и на внутренность угла, ограниченного лучами и .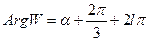

Очевидно, отображение 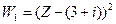переведет угол плоскости Z на угол, ограниченный лучам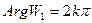и и 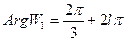. Повернем полученный угол на . Произведем теперь отображение 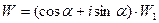. Оно переведет лучи плоскости 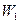в лучи и 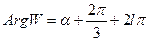. Следовательно, отображение W, равное и будет искомым.

Множество G называется группой, если в нем определена операция умножения, ставящая в соответствие каждой паре x,y некоторый, вполне определенный элемент z, также принадлежащий G, называемый произведением элементов x и y и обозначаемый символом xy, и выполняются следующие свойства:

1. Для любого выполняется равенство (x·y)·z=x·(y·z) (ассоциативность).

2. Существует элемент e G такой, что для любого , выполняется равенство e·x = x·e = x (e – единичный элемент).

3. Для любого существует элемент , называемый обратным элементом, такой, что x^-1·x=x· x^-1 = e.

Если еще для любых 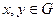x·y=y·x, то группа Абелева или коммутативна.

Рассмотрим множество G всевозможных дробно-линейных функций

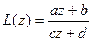(1)

с определителем . Покажем, что в этом множестве G можно ввести операцию умножения, таким образом, что G станет группой.

Вначале отметим, что два отображения 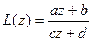и 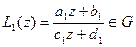мы будем считать равными, если при всех 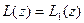. Очевидно, если существует комплексное число 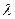, такое, что

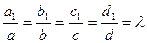(2),

то эти два отображения будут совпадать.

Покажем, что условие (2) является и необходимым для равенства отображени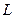й и 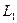. Так как определитель , то, по крайней мере, одно из чисел a или c не равно нулю.

Пусть для определенности . Пусть 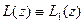. Покажем, что выполняется соответствие (2). Очевидно 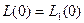, поэтому 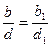, следовательно, (3). Аналогично , следовательно, 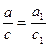и, значит (4).

Легко видеть, что при , , 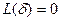поэтому 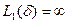, а это значит, что , поэтому 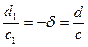. Отсюда следует, что

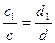(5).

Из (3), (4), (5) и следует (2). (Если 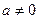, то поменять числитель и знаменатель ролями).

Мы знаем, что дробно-линейная функция 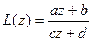с определителем конформна в расширенной плоскости (Z).

Покажем, что функция осуществляет взаимно однозначное отображение плоскости (Z) на плоскость (W). Действительно каждая точка W плоскости (W) имеет в плоскости (Z) единственный прообраз 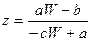(6). Следовательно, отображение является взаимно однозначным.

Отображение (6) мы будем называть обратным по отношению к и будем писать .

Введем теперь во множество G – произведение двух отображени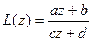й и 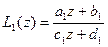по формуле

,

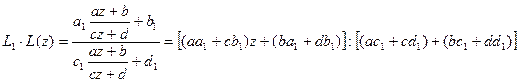мы получим дробно-линейную функцию. Ее определитель

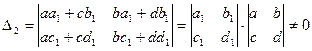(так как ),

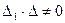следовательно, .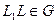

Покажем, что это множество дробно-линейных функций с введенной операцией умножения (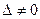) является группой.

Три свойства группы:

1. Пусть дробно-линейные функции (принадлежит множеству дробно-линейных функций с 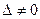). Покажем, что выполняется равенство

(1),

для этого значения в любой точке должны быть равны.

Возьмем производную в точке 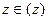(комплексной плоскости) и обозначим через значение 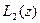, будем иметь

(2)

и по определению произведения

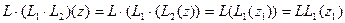(3).

Так как правые части равенств (2) и (3) равны, то будут равны и левые части этих равенств. Отсюда из произвольности выбора z и следует справедливость равенства (1). Следовательно, первое групповое свойство для множества M выполняется.

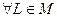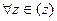2. Покажем, что тождественное отображение является единичным элементом в M. То есть, что для выполняется равенство (4). Очевидно, для выполняются равенства 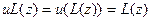и . Так как правые части последних равенств равны, то справедливы (4). Следовательно, u является единичным элементом во множестве M.

3. Возьмем произвольное 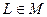, как мы знаем, у рассматриваемого отображения L существует обратное отображение 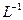, которое также является дробно-линейным и определитель которого не ранен нулю, то есть 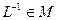. Покажем, что это отображение 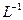и будет обратным элементом для L, то есть выполняются равенства:

(5).

Возьмем любую точку 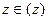. Пусть , тогда по определению обратной функции будет 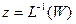. Значит . Возьмем теперь произвольную точку W. Пусть 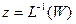по определению обратной функции . Значит 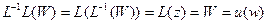. Из последних двух равенств вытекает равенство (5).

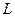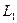
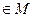Следовательно, множество M удовлетворяет всем свойствам определения группы, поэтому оно является группой. Эта группа не является абелевой или коммутативной. Очевидно, нам достаточно указать, что существуют отображения и , что .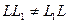

Пусть , а . Посчитаем произведение. Очевидно .

Аналогично .

Как видно, правые части двух последних равенств различны (тождественно не совпадают), поэтому выполняется неравенство 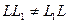, то есть группа M не является абелевой.

Дата добавления: 2015-06-26