Розрахунок

Приклад розрахунку

Консольна балка, виконана з сталевого профілю «двотавр». Навантаження складається з моменту М і двох сил:F₁ та F₂. Сила F₂ діє під кутом α. Лінійні ділянки балки мають довжину l. Опора A– нерухомий шарнір. Опора B – рухомий шарнір.

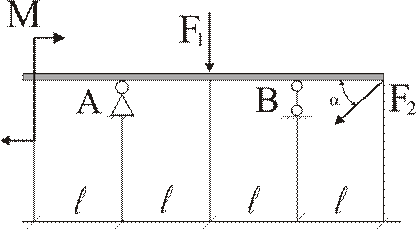
Рис. 3 – Схема балки.

Вихідні дані: M = 40 кНм; F₁ = 60 кН; α = 60˚; l = 2м; F₂ = 40 кН; профіль-двотавр.

1. Балка є нерухомою, тоді з умови її рівноваги під дією прикладеного навантаження та реакцій опор можливо визначити ці реакції.

2. Запроваджуємо систему координат Z,Y. Звільняємо балку від в’язів і замінюємо їх реакціями R_AZ, R_AY, R_BY (невідома реакція R_A розкладена на дві складові R_AZ та R_AY, а реакція опори B – R_BY має лінію дії вздовж осі Y, тобто перпендикулярно напрямку рухомості опори (Рис – 4.а).

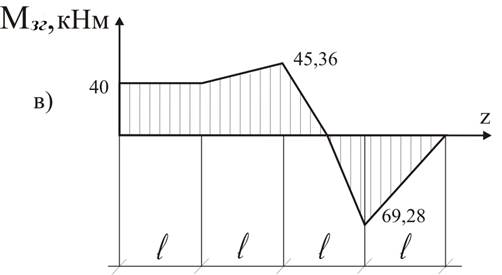
Рис.4 (а,б,в) – Схема навантаження балки та епюри поперечних силі згинальних моментів.

3. Рівняння рівноваги мають вигляд:

Σ F_Zi=0; R_AZ – F₂cosα = 0 (1)

Σ M_A = 0; –M – F₁· l + R_BY 2· l – F₂ 3· l sinα = 0 (2)

Σ M_B= 0; –M – R_AY 2· l + F₁· l – F₂· l sinα = 0 (3)

4. Розв’язуємо рівняння:

R_AZ = F₂cos α = 40cos60˚ = 20кН

R_BY =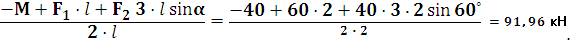

R_AY = кН.

Перевірка:Σ F_y =0 = R_AY – F₁ + R_BY – F₂ sin α = 2,68–60+91,96–34,63 0

5. Будуємо епюру поперечних сил починаючи з лівого кінця балки (Рис.4.б) (напрям осі Yприйнято за позитивний).

6. Будуємо епюру згинальних моментів (Рис. 4.в). Побудову також починаємо з лівого краю, де прикладений момент M= 40 кНм. Використовуємо правило знаків: «момент, який згинає балку опуклістю до гори, вважаємо від’ємним і навпаки».

Поперечні перерізи балки позначимо номерами: 1, 2, 3, 4, 5.

- Ділянка балки між перерізами 1 і 2 навантажена моментом

M= 40кНм.

- Переріз 3 навантажений згинальним моментом

M₃ = M + R_AY· l = 40+2,68·2=45,36 кНм.

- Переріз 4 навантажений згинальним моментом

M₄ = M + R_AY 2· l –F1 l = 40+2,68·2·2-60·2 = -69,28 кНм.

- Переріз 5 навантажений нульовим згинальним моментом.

7. Небезпечним, де діє максимальний за модулем згинальний момент є переріз 4 (M₄ = 69,28 кНм.)

8. За умови міцності матеріалу балки на згин визначаємо величину потрібного моменту опору перерізу та номер профілю двотавра.

Для прокату зі сталі (Ст.3)прийнято брати допустимі напруження:

[ ] = 150 Мпа і[ = 100 Мпа, (1 МПа = 1).

Таким чином, момент опору потрібного перерізу з умови забезпечення міцності дорівнює: 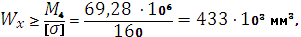або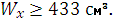

По таблиці сортаменту [3] підбираємо двотавр №30, у якого

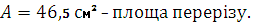B = 6,5 – товщина стінки. (Рис. 5)

Рис. 5 Переріз двотаврової балки.

9. Визначаємо максимальні розрахункові напруження

- нормальні напруження від згину

- дотичні напруження від дії поперечних сил.

Для цього використовуємо формулу Журавського [2]: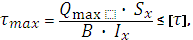

де Q_max = 57.32 кН – найбільша поперечна сила (див. епюру поперечних сил);

S_X – статичний момент половини перерізу;

I_x – момент інерції перерізу;

B – товщина вертикальної стінки.

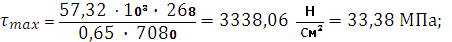тобто

Таким чином, розміри перерізу балки задовольняють умовам міцності як за нормальними, так і за дотичними напруженнями. З розрахунку видно, що максимальні дотичні напруження майже у 5 разів менше за поперечні, тому зазвичай ними нехтують.

Запитання для самоконтролю:

1. Назвіть основні питання, які розглядаються в розділі «Опір матеріалів» курсу «Теоретична і прикладна механіка».

2. Сформулюйте основні поняття опору матеріалів:

- Міцність;

- Жорсткість;

- Стійкість.

3. Які основні види деформацій, вам відомі?

4. Що таке нормальні напруження?

5. Що таке дотичні напруження?

6. Який згин вважають «чистим», а який «поперечним»?

7. Які характеристики поперечних перерізів вам відомі?

8. Які типи опор балок, вам відомі і які реакції виникають в цих опорах під дією зовнішніх сил і моментів?

9. Яке правило знаків використовують при побудові епюри згинальних моментів?

10. Як записати умову міцності при «чистому» згині?

11. Що таке «допустиме напруження» і як його визначають для пластичних і крихких матеріалів.

12. Запишіть умови рівноваги твердого тіла, навантаженою довільною системою сил і моментів.

Список рекомендованої літератури:

1. Путята Т.В., Можаровський Н.С. и др. Прикладна механіка – К.: Вища школа. 1977 р. – 535 с.

2. Писаренко Г.С., Квітка О.Л., Уманський Е.С. Опір матеріалів. – К.: Вища школа. 1993 р. – 655 с.

3. Писаренко Г.С., Яковлева А.П., Матвеев В.В., Справочник по сопротивлению материалов. – К.: Наукова думка. 1975 р. – 704 с.

Дата добавления: 2015-06-04