Теоретичні відомості. Визначення моменту інерції тіла довільної форми

Відносно обраної осі

Визначення моменту інерції тіла довільної форми

Контрольні питання

1. Який удар називається абсолютно пружним?

2. Який удар називається абсолютно непружним?

3. Який удар називається центральним?

4. Що називається імпульсом тіла?

5. Як формулюється закон збереження імпульсу?

6. Яка система тіл називається замкненою?

7. Отримайте формулу швидкості куль після непружного удару.

8. Яка енергія називається потенціальною?

9. Як формулюється закон збереження повної механічної енергії і загальний закон збереження та перетворення енергії?

10. Як обчислити дисипацію енергії при непружному ударі?:

а) за різницею швидкостей до і після удару;

б) за різницею кінетичних енергій куль до і після удару;

в) за величиною імпульсу куль до і після удару;

г) за величиною кута відхилення куль до і після удару.

Лабораторна робота № 103

Мета роботи: Визначити моменти інерції тіла відносно різних осей.

Питання курсу, рекомендовані для вивчення перед виконанням роботи:

Обертальний рух точки та системи матеріальних точок. Момент сили та імпульсу тіла відносно полюса (нерухомої точки). Рівняння моментів. Закон збереження моменту імпульсу. Обертання твердого тіла. Основне рівняння динаміки обертального руху твердого тіла навколо нерухомої осі. Момент інерції. Момент імпульсу та кінетична енергія твердого тіла, що обертається навколо осі.

Основне рівняння динаміки обертального руху твердого тіла навколо нерухомої осі можна записати у вигляді:

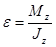, (1)

де 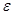- кутове прискорення, - результуючий момент сил відносно осі обертання z, J_z – момент інерції тіла відносно цієї осі.

З цього рівняння видно, що кутове прискорення 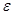, набуте твердим тілом, яке обертається навколо нерухомої осі, прямо пропорційне результуючому моменту всіх зовнішніх сил відносно осі обертання та обернено пропорційне моменту інерції тіла відносно цієї осі.

Моментом сили відносно осі z називається скалярна фізична величина, яка чисельно дорівнює проекції вектора моменту сили відносно полюса (нерухомої точки), що лежить на осі на цю вісь. Можна довести, що величина моменту сили відносно осі завжди буде дорівнювати добутку модуля складової сили, перпендикулярної осі , на найменшу відстань між віссю і лінією дії сили (плече сили):

.

Момент інерції тіла відносно осі z – це фізична величина, яка чисельно дорівнює сумі добутків мас всіх часток твердого тіла на квадрат їх відстаней до осі обертання:

J_z = 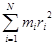. (4)

З рівняння (1) випливає, що

J_z = 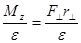. (4а)

У даній лабораторній роботі момент сил, що діє на систему, можна визначити з наступних міркувань: момент сил утворюється силою натягу нитки l, навитої на шків (рис. 1). Так як момент сили тертя, прикладеної до шківа, значно менший за момент сили натягу нитки, то у подальших розрахунках їм можна знехтувати.

Позначимо силу натягу нитки через , а плече цієї сили через D/2, де D – діаметр шківа. Тоді

М= · 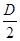. (5)

Силу натягу нитки можна знайти з рівняння руху вантажу:

. (6)

Перейдемо від векторної форми запису рівняння руху вантажу до скалярної. Спроектуємо всі вектори на напрямок х (рис.1):

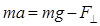. (7)

Звідси сила натягу нитки: = m(g-a). (8)

Прискорення a вантажу m, що спускається зі стану спокою на відстань h, може бути легко знайденим за формулою:

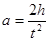, (9)

де t – час спуску вантажу.

Лінійне прискорення вантажу m дорівнює лінійному прискоренню точок поверхні шківу, з якого змотується нитка при спуску вантажу. Тому кутове прискорення обертової частини приладу може бути знайденим з співвідношення:

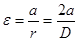. (10)

Підставляючи в рівняння (4а) вираз для F та ε з формул (8) і (10), одержимо розрахункову формулу для J в такому вигляді:

J = . (11)

В умовах цієї роботи >> 1, тому остаточно маємо:

. (12)

Опис лабораторної установки

Установка для вимірювання моменту інерції (рис. 1) складається з диску, на якому закріплено тіло, що досліджується. Диск приводиться до обертання при спуску вантажу m, який прикріплений до нитки, намотаної на шків. Шків та диск насаджені на одну вісь обертання.

Методика вимірювання

За формою тіло, що досліджується, є прямокутним паралелепіпедом. Необхідно визначити момент інерції цього тіла відносно кожної з трьох взаємно перпендикулярних осей, що проходять через центр мас тіла паралельно його ребрам.

Розрахунок моменту інерції проводиться за формулою (12). Висота h спуску вантажу m вимірюється лінійкою, що знаходиться на установці. Час спуску визначається автоматичним електричним секундоміром.

Прискорення земного тяжіння прийняти рівним 9,8 м /с². D – діаметр шківу, вимірюється штангенциркулем.

Прилади та обладнання: Установка для вимірювання моменту інерції; тіло, що досліджується; автоматичний електричний годинник; штангенциркуль, комплект вантажів.

Порядок виконання роботи

1. Вимірити штангенциркулем діаметр шківу.

2. Виписати висоту спуску вантажу m та момент інерції установки J₀ без досліджуваного тіла, які вказані на установці.

3. Виміряти час спуску t вантажу m та знайти середнє значення < t >.

4. Виміряти момент інерції приладу разом з розташованим на ньому досліджуваним тілом при трьох різних положеннях тіла J ^/, J ^//, J ^///. Віднімаючи від результатів вимірювання J ^/, J ^//, J ^/// момент інерції J₀ незавантаженої установки, обчислити моменти інерції досліджуваного тіла відносно трьох осей обертання J₁, J₂, J₃.

5. Порівнюючи між собою знайдені моменти інерції досліджуваного тіла, визначити, по відношенню до яких осей момент інерції тіла має максимальне і мінімальне значення.

Таблиця результатів вимірювань

№№	m, кг	Δ m, кг	D, м	ΔD, м	h, м	Δh, м	t, c	Δt, c
без тіла	з тілом
1 вісь	2 вісь	3 вісь
1. 2. 3.

Таблиця результатів розрахунків

J0, кг·м^2	J ^/, кг·м^2	J ^//, кг·м^2	J ^///, кг·м^2	J1, кг·м^2	J2, кг·м^2	J3, кг·м^2

Контрольні питання

1.Записати і сформулювати основне рівняння динаміки обертального руху.

2.Що називається моментом сили відносно осі? В яких одиницях він вимірюється?

3.Що називається плечем сили? Як воно визначається в даній роботі?

4.Що називається моментом інерції тіла відносно осі обертання? В яких одиницях він вимірюється?

5.Яку властивість тіла характеризує момент інерції?

6.Від чого залежить момент інерції тіла?

7.Під впливом моменту якої сили диск приходить в обертальний рух?

8.Як в даній роботі можна змінити обертальний момент?

- змінивши радіус шківу;

- змінивши висоту падіння вантажу;

- змінивши масу падаючого вантажу;

- змінивши масу тіла, закріпленого на диску;

- змінивши вісь обертання тіла, закріпленого на диску.

Лабораторна робота № 104

Вивчення основного закону обертального руху

Мета роботи:

1. Перевірити залежність .

2. Визначити момент інерції системи при різних розподілах її маси відносно осі обертання.

Питання курсу, рекомендовані для вивчення перед виконанням роботи:

Обертальний рух точки та системи матеріальних точок. Момент сили та імпульсу тіла відносно полюса (нерухомої точки). Рівняння моментів. Закон збереження моменту імпульсу. Обертання твердого тіла. Основне рівняння динаміки обертального руху твердого тіла навколо нерухомої осі. Момент інерції. Момент імпульсу та кінетична енергія твердого тіла, що обертається навколо осі.

Дата добавления: 2015-06-26