Аналітичне вирівнювання ряду динаміки

Найбільш точним і ефективним способом виявлення основної тенденції розвитку є аналітичне вирівнювання. При цьому фактичні рівні ряду динаміки замінюються теоретичними рівнями, обчисленими на основі певної кривої, що описується аналітичним виразом. Передбачається, що теоретична крива вільна від всіляких коливань і тому найточніше відображає загальну тенденцію зміни в часі показника, що вивчається.

При аналітичному вирівнюванні ряду динаміки, його рівні виражаються у вигляді функції часу.

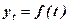(13.1)

де 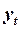– теоретичний рівень ряду динаміки, обчислений по визначеному

аналітичному виразу на момент часу .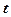

Найчастіше всього при аналітичному вирівнюванні використовуються наступні математичні залежності:

- лінійна (рівняння прямої):

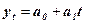(13.2)

- параболічна (рівняння параболи):

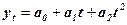(13.3)

- експоненціальна (рівняння експоненти):

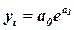(13.4)

- гіперболічна (рівняння гіперболи):

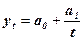(13.5)

Вибір форми кривої багато в чому визначає результати виявлення тренда. Основою для вибору форми кривої може використовуватися змістовний аналіз суті розвитку даного явища. Можна спиратися на результати попередніх досліджень у даній області.

На практиці для цих цілей удаються до аналізу графічного зображення рівнів ряду динаміки (лінійної діаграми). Проте з графічного представлення емпіричних даних не завжди вдається провести однозначний вибір форми кривої (виду рівняння). Тому доцільно скористатися графічним зображенням згладжених рівнів, в яких випадкові та періодичні коливання в деякій мірі виявляються згладженими.

При виборі виду аналітичної кривої для вирівнювання ряду динаміки можна скористатися наступними рекомендаціями.

1. Лінійна залежність використовується в тому випадку, коли в початковому ряду динаміки спостерігається більш менш постійні абсолютні ланцюгові прирости, що не проявляють тенденції ні до збільшення, ні до зниження.

2. Параболічна залежність вибирається в тих випадках, коли абсолютні ланцюгові прирости самі по собі виявляють деяку тенденцію розвитку, але абсолютні ланцюгові прирости абсолютних приростів (різниці другого порядку) ніякої тенденції розвитку не проявляють.

3. Експоненціальні залежності, якщо в початковому динамічному ряду спостерігається або більш менш постійне відносне зростання (стійкість ланцюгових темпів зростання, темпів приросту, коефіцієнтів зростання), або, за відсутності точної постійності, – стійкість у зміні показників відносного зростання (ланцюгових темпів зростання ланцюгових же темпів зростання).

Для вирішення рівнянь аналітичних кривих (формули 13.2 – 13.5) у більшості випадків використовують метод найменших квадратів, який забезпечує найменшу суму квадратів відхилень фактичних рівнів від вирівняних (теоретичних).

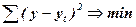(13.6)

Розглянемо техніку аналітичного вирівнювання ряду динаміки з використанням рівняння прямої, що має найбільш простий вираз, на наступному прикладі.

Приклад. Є дані за останні 10 років по заводу, де виготовляють запасні частини для тракторів. Ці дані приведені в табл. 13.3.

1. Для того, щоб висунути гіпотезу про передбачуваний закон розподілу рівнів ряду динаміки, побудуємо графік залежності випуску продукції від часу. Такий графік для нашого прикладу представлений на рис. 13.1.

Таблиця 13.3

Випуск продукції на заводі (тис. шт.)

Роки	Випуск продукції ()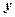
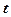
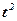
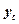
	39,4	-9		-354,60	39,43
	39,8	-7		-278,60	39,84
	40,0	-5		-200,00	40,25
	40,6	-3		-121,80	40,66
	41,4	-1		-41,40	41,07
	41,9	+1		41,90	41,47
	41,9	+3		125,70	41,88
	42,0	+5		210,00	42,29
	42,6	+7		298,20	42,70
	43,1	+9		387,90	43,11
Разом:	412,7			67,30	412,70

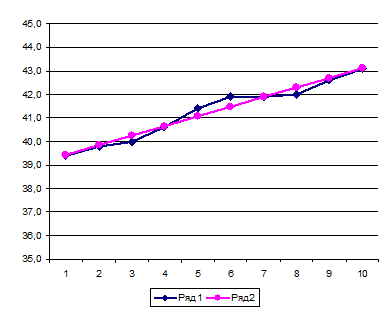
Рис. 13.1. Динаміка випуску продукції за роками

(ряд 1 – фактичні дані (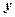); ряд 2 – вирівняні дані ()).

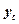2. За характером фактичних рівнів, приймаємо гіпотезу про існування прямолінійного тренда (динаміка випуску характеризується прямою лінією).

3. Запишемо рівняння прямої .

4. Вирішити це рівняння – означає знайти параметри 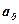і 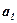шуканої прямої. Найпростіше знайти значення цих параметрів можна, скориставшись методом найменших квадратів. Для цього необхідно вирішити систему нормальних рівнянь:

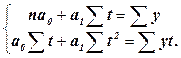(13.7)

де 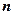– число членів ряду динаміки;

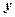– фактичні рівні ряду динаміки.

Система рівнянь спрощується, якщо 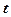підібрати так, щоб їх сума дорівнювала нулю, тобто початок відліку часу перенести в середину даного періоду. Тод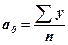і:

і 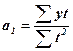(13.8, 13.9)

У табл. 13.3 проводимо необхідні розрахунки й тод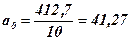і:

і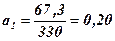

Підставимо знайдені параметри 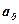і 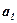в рівняння прямої. Шукане рівняння матиме вигляд:

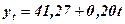
За допомогою рівняння знайдемо розрахункові значення вирівняних рівнів ряду динаміки, підставляючи в нього значення 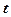з табл. 13.3.

Отримане рівняння, що описує досліджуваний ряд динаміки, показує, що середній рівень виробництва деталей складає 41,27 тис. шт. в рік і щорічно збільшується в середньому на 0,20 тис. штук в рік. Сума рівнянь емпіричного ряду повністю співпадає з сумою розрахункових значень вирівняного ряду.

Аналогічним чином проводиться аналітичне вирівнювання рядів динаміки з використанням інших рівнянь кривих. Проте кожній кривій відповідає своя система нормальних рівнянь. Так, наприклад, для вирішення рівняння параболи система рівнянь має вигляд:

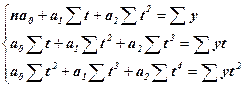(13.10)

Для вирішення експоненціального рівняння, система нормальних рівнянь має вигляд:

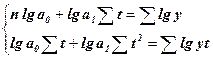(13.11)

Питання для самоконтролю

Дата добавления: 2015-06-26