Уравнение линии уровня, проходящей через данную точку, будет

.

Задание для самостоятельной работы

106. Найти производную функции в точке М (2; 1) в направлении вектора S = i +2 j.

107. Найти производную функции 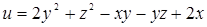в точке М (3; 1; 5) в направлении вектора S = i - 2 j + 3 k.

108. Найти производную функции 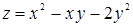в точке P (1; 2) в направлении, составляющем с осью Ox угол в 60°.

109. Найти производную функции 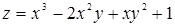в точке M (1; 2) в направлении, идущем от этой точки к точке N (4; 6).

110. Найти производную функции в точке М (1; 1) в направлении биссектрисы первого координатного угла.

111. Найти производную функции 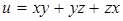в точке M (2; 1; 3) в направлении, идущем от этой точки к точке N (5; 5; 15).

112. Найти градиент функции в точке P (2; 1).

113. Найти градиент функции 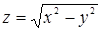в точке P (5; 3).

114. Найти градиент функции в точке P (1; 2; 3).

115. Найти угол между градиентами функций и в точке P (3; 4).

12. Формула Тейлора для функции двух переменных

Пусть функция двух переменных z = f (х, у) непрерывна вместе со всеми частными производными до (п + 1)-го порядка включительно в некоторой окрестности точки М (а, b). Тогда функцию двух переменных представим в виде суммы многочлена п -го порядка по степеням х – а и у – b и некоторого остаточного члена. Для случая п = 2 эта формула имеет вид

, (41)

где коэффициенты А ₀, D, E, А, В, С не зависят от х и у, а R ₂ – остаточный член, структура которого аналогична структуре остаточного члена в формуле Тейлора для функции одной переменной.

Применим формулу Тейлора для функции f (х, у) одной переменной у, считая х постоянным (ограничимся членами второго порядка):

, (42)

где h₁ = b + q₁(у – b), 0 < q₁ < 1. Функции f (x, b), f_y ¢(x, b), 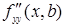разложим по формуле Тейлора по степеням х – а, ограничиваясь смешанными производными до третьего порядка включительно:

, (43)

где x₁ = х + q₂(х – а), 0 < q₂ < 1;

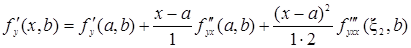, (44)

где x₂ = х + q₃(х – а), 0 < q₃ < 1;

, (45)

где x₃ = х + q₄(х – а), 0 < q₄ < 1.

Подставляя выражения (43), (44) и (45) в формулу (42), получим

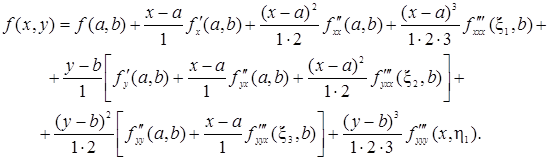
Располагая слагаемые так, как указано в формуле (41), получим

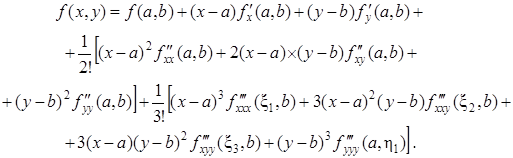(46)

Это и есть формула Тейлора при п = 2. Выражение

называется остаточным членом.

Обозначим, далее, х– а = D х, у – b = D у, 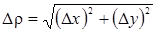. Преобразуем R ₂:

Так как ½D х ½< Dr,½D у ½< Dr и третьи производные, по условию ограничены, то коэффициент Dr³ ограничен в рассматриваемой области; обозначим его через a₀.

Тогда можно написать

R ₂ = a₀ Dr³.

Формула Тейлора (46) в принятых обозначениях для случая п = 2 примет вид

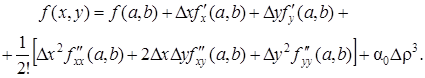
При любом п формула Тейлора имеет аналогичный вид.

Задание для самостоятельной работы

116. Разложить по целым положительным степеням k и h, если .

117. Разложить функцию 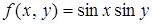по степеням и . Найти члены первого и второго порядка и (остаточный член второго порядка).

118. Функцию 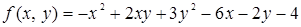разложить по формуле Тейлора в окрестности точки (-2; 1).

119. Найти приращение, получаемое функцией 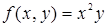при переходе от значений x = 1, y = 1 к значениям x = 1 + h, y = 1 + k.

120. Найти приращение, получаемое функцией

при переходе от значений x = 1, y = 2 к значениям x = 1 + h, y = 1 + k. Ограничиваясь членами 2-го порядка включительно, вычислить f (1,02; 2,03).

121. Разложить по формуле Тейлора в окрестности точки (1; 1) до членов 2-го порядка включительно функцию .

122. Разложить по формуле Тейлора в окрестности точки (1; -1) до членов 3-го порядка включительно функцию .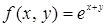

123. Вывести приближенную формулу с точностью до членов 2-го порядка относительно величин a и b для выражения .

124. Используя формулу Тейлора до членов 2-го порядка, вычислить приближенно .

125. Разложить в ряд Тейлора при a = 0, b = 0 функцию

.

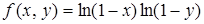13. Максимум и минимум функции нескольких переменных

Определение 1. Мы говорим, что функция z = f (х, у) имеет максимум в точке М ₀(х ₀, у ₀) (т.е. при х = х ₀, у = у ₀), если

f (х ₀, у ₀) > f (х, у)

для всех точек (х, у), достаточно близких к точке (х ₀, у ₀) и отличных от нее.

Определение 2. Совершенно аналогично говорят, что функция z = f (х, у) имеет минимум в точке М ₀(х ₀, у ₀), если

f (х ₀, у ₀) < f (х, у)

для всех точек (х, у), достаточно близких к точке (х ₀, у ₀) и отличных от нее.

Максимум и минимум функции называются экстремумами функции, т.е. говорят, что функция имеет экстремум в данной точке, если эта функция имеет максимум или минимум в данной точке.

Пример 40. Функция достигает минимума при х = 1, у = 2, т.е. в точке (1, 2). Действительно, f (1, 2) = -1, а так как (х – 1)² и (у – 2)² всегда положительны при х ¹ 1, у ¹ 2, то (х – 1)² + (у – 2)² – 1 > -1, т.е. f (х, у) > f (1, 2).

Пример 41. Функция при х = 0, у = 0 (т.е. в начале координат) достигает максимума.

Действительно, f (0, 0) = ½. Возьмем внутри окружности х ² + у ² = p/6 точку (х, у), отличную от точки (0, 0); тогда при 0 < х ² + у ² < p/6 будет sin(х ² + у ²)> 0 и поэтому 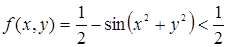, т.е. f (х, у) < f (0, 0).

Данное выше определение максимума и минимума функции можно перефразировать следующим образом.

Положим х = х ₀ + D х, у = у ₀ + D у; тогда

.

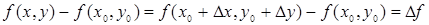1. Если D f < 0 при всех достаточно малых приращениях независимых переменных, то функция f (х, у) достигает максимума в точке М ₀(х ₀, у ₀).

2. Если D f > 0 при всех достаточно малых приращениях независимых переменных, то функция f (х, у) достигает минимума в точке М ₀(х ₀, у ₀).

Эти формулировки переносятся без изменения на функцию любого числа переменных.

Теорема 1 (необходимое условие экстремума). Если функция z = f (х, у) достигает экстремума при х = х ₀, у = у ₀, то каждая частная производная первого порядка от z или обращается в нуль при этих значениях аргументов, или не существует.

Действительно, дадим переменной у определенное значение, именно у = у ₀. Тогда функция f (х, у ₀) будет функцией одной переменной х. Так как при х = х ₀ она имеет экстремум (максимум или минимум), то, следовательно, или равно нулю, или не существует. Совершенно аналогично можно доказать, что или равно нулю, или не существует.

Эта теорема не является достаточной для исследования вопроса об экстремальных значениях функции, но позволяет находить эти значения в тех случаях, в которых мы заранее уверены в существовании максимума или минимума. В противном случае требуется дополнительное исследование.

Так, например, функция z = x ² – y ² имеет производные 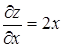, , 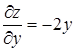которые обращаются в нуль при х = 0 и у = 0. Но эта функция при указанных значениях не имеет не максимума, ни минимума. Действительно, эта функция равна в нулю в начале координат и принимает в как угодно близких точках от начала координат как положительные, так и отрицательные значения. Следовательно, значение нуль не является ни максимум ни минимум.

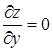Точки, в которых (или не существует) и (или не существует), называются критическими точками функции z = f (х, у). Если функция достигает экстремума в какой-либо точке, то (в силу теоремы 1) это может случиться в критической точке.

Для исследования функции в критических точках установим достаточные условия экстремума функции двух переменных.

Теорема 2. Пусть в некоторой области, содержащей точку М ₀(х ₀, у ₀), функция f (х, у) имеет непрерывные частные производные до третьего порядка включительно; пусть, кроме того, точка М ₀(х ₀, у ₀) является критической точкой функции f (х, у), т.е.

, .

Тогда при х = х ₀, у = у ₀

1) f (х, у) имеет максимум, есл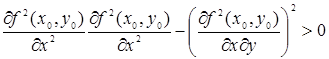и

и ;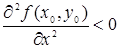

2) f (х, у) имеет минимум, есл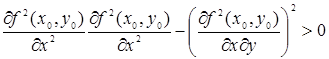и

и ;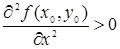

3) f (х, у) не имеет ни максимум, ни минимума, если

;

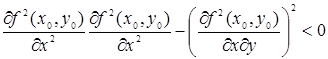4) если 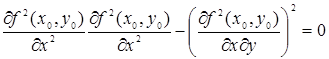, то экстремум может быть и может не быть (в этом случае требуется дополнительное исследование).

Доказательство. Напишем формулу Тейлора второго порядка для функции f (х, у). Полагая а = х ₀, b = у ₀, х = х ₀ + D х, у = у ₀ + D у, будем иметь

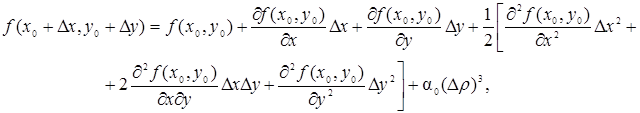
где 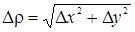, а a₀ стремится к нулю при Dr ® 0.

По условию

, .

Следовательно,

(47)

Обозначим теперь значения вторых частных производных в точке М ₀(х ₀, у ₀) через А, В, С:

, , .

Обозначим через j угол между направлением отрезка М ₀ М, где М есть точка М (х ₀ + D х, у ₀ + D у), и осью Ох; тогда D х = Dr cosj, D у = Dr sinj. Подставляя эти выражения в формулу (47), найдем

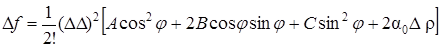. (48)

Предположим, что А ¹ 0.

Разделив и умножив на А выражение, стоящее в квадратных скобках, получим

. (49)

Рассмотрим теперь четыре возможных случая.

1. Пусть АС – В ² > 0, А < 0. Тогда в числителе дроби стоит сумма двух неотрицательных величин. Они одновременно в нуль не обращаются, так как первый член обращается в нуль при tg j = - А/В, второй при sin j = 0.

Если А < 0, то дробь есть отрицательная величина, не обращающаяся в нуль. Обозначим ее через – т ²; тогда

,

где т не зависит Dr, a₀Dr ® 0 при Dr ® 0. Следовательно, при достаточно малых Dr будет D f < 0, или f (х ₀ + D х, у ₀ + D у) – f (х ₀, у ₀) < 0. Но тогда для всех точек (х ₀ + D х, у ₀ + D у), достаточно близких к точке (х ₀, у ₀), имеет место неравенство

f (х ₀ + D х, у ₀ + D у) < f (х ₀, у ₀),

а это означает, что в точке (х ₀, у ₀) функция f (х, у) достигает максимума.

2. Пусть АС – В ² > 0, А > 0. Тогда, рассуждая аналогично, получим

,

или

f (х ₀ + D х, у ₀ + D у) > f (х ₀, у ₀),

т.е. f (х, у) имеет минимум в точке (х ₀, у ₀).

3. Пусть АС – В ² < 0, А > 0. В этом случае функция не имеет ни максимума ни минимума. Функция возрастает, когда мы движемся из точки (х ₀, у ₀) по одним направлениям, и убывает, когда мы движемся по другим направлениям. Действительно, при перемещении вдоль луча j = 0 имеем

;

при движении вдоль этого луча функция возрастает. Если же перемещаться вдоль луча j = j₀ такого, что tg j₀ = - А/В, то при А > 0 будет

;

при движении вдоль этого луча функция убывает.

Пусть АС – В ² < 0, А < 0. В этом случае функция тоже не имеет ни максимума, ни минимума. Исследование проводится так же, как и в рассматриваемом ранее случае.

Пусть АС – В ² < 0, А = 0. Тогда В ¹ 0, и равенство (48) можно переписать в виде

.

При достаточно малых значениях j выражение, стоящее в круглых скобках, сохраняет знак, так как оно близко к 2 В, а множитель sin j меняет знак в зависимости от того, будет ли j больше нуля или меньше нуля (после выбора j > 0 и j < 0 мы можем r взять настолько малым, что 2a₀ не будет изменять знак всей квадратной скобки). Следовательно, и в этом случае D f меняет знак при различных j, т.е. при различных D х и D у, следовательно, и в этом случае нет ни максимума, ни минимума.

Таким образом, каков бы ни был знак А, имеем всегда следующее положение:

Если АС – В ² < 0 в точке (х ₀, у ₀), то функция не имеет в этой точке ни максимума, ни минимума. Говорят, что функция имеет в этой точке минимакс.

4. Пусть АС – В ² = 0. В этом случае на основании формул (48) и (49) сделать заключение о знаке D f нельзя. Так, например, при А ¹ 0 будем иметь

;

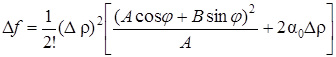при j = arctg (- А/В) знак D f определяется знаком 2a₀, здесь требуется специальное дальнейшее исследование (например, с помощью формулы Тейлора более высокого порядка или каким-либо иным способом). Таким образом, теорема 2 полностью доказана.

Пример 42. Исследовать на максимум и минимум функцию

.

Решение. 1. Находим критические точки:

, .

Решая систему уравнений

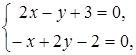
получаем

, .

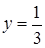2. Находим производные второго порядка в критической точке (-4/3; 1/3) и определяем характер критической точки:

, , ,

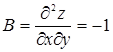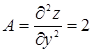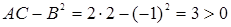, А > 0.

Следовательно, в точке (-4/3; 1/3) данная функция имеет минимум, а именно:

.

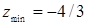Замечание. Теория максимумов и минимумов функции нескольких переменных является основой для одного метода получения формул для изображения функциональных зависимостей на основании экспериментальных данных.

Задание для самостоятельной работы

Исследовать на экстремум следующие функции:

126. .	127. .
128. .	129. .
130. 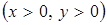.	131. .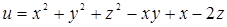
132. 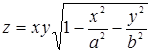.	133. .
134. .	135. .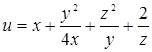

Дата добавления: 2015-06-04