WTA типті нейрондар

WTA типті нейрондарда (Winner Takes All – Жеңімпаз барлығын алады) шығыс сигналдарының мәнін сәйкес үлестерімен қосындыларын есептейтін стандартты сумматор түріндегі кіріс модулі бар. І-ші сумматордың шығыс сигналы (13.22) формулаға сәйкес есептелінеді

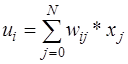. (13.22)

Өзара бәсекелес нейрондар тобы (13.9-сурет) бір x_j кіріс сигналдарын алады. Үлес коэффициенттерінің нақты мәндеріне байланысты жекелеген нейрондардың u_i қосынды сигналдары әртүрлі болуы мүмкін. Осы сигналдарды салыстырудың нәтижесінде u_i мәні ең үлкен болған нейрон жеңімпаз деп саналады. Жеңімпаз-нейрон өз шығысында 1 күйін, ал қалған (жеңілген) нейрондар 0 күйіне өтеді.

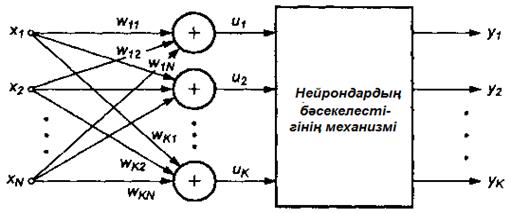
13.9-сурет. WTA типті нейрондардың қосылу сұлбасы

WTA типті нейрондарды оқыту үшін мұғалім қажет емес, ол х қалыптанған (нормальденген) кіріс векторын қолдану арқылы жүреді. Бастапқы кезеңде әрбір нейронның 1 қатысты қалыптанатын үлес коэффициенттері кездейсоқ таңдалынады. Бірінші х кіріс векторы берілгеннен кейін жеңімпаз анықталады. Жеңімпаз болған нейрон 1 күйіне өтеді, ал бұл оған оның кіріс түзулерінің үлестерін нақтылауға мүмкіндік береді (Гроссберг ережесі бойынша).

Жеңілген нейрондар шығыстарында 0 күйін қалыптастырады, ал бұл болса үлес коэффициенттерін нақтылау үдерісін жүзеге асыруды бұғаттайды. Бәсекелесуші нейрондардың (0 немесе 1) шығыс сигналдары мәндерінің бинарлығының салдарынан Гроссберг ережесі біраз қысқарады:

. (13.23)

WTA типті нейрондардың қызмет етуіне кіріс векторларымен үлес коэффициенттерін қалыптандыру бірталай әсер етеді. І-ші нейронның шығыс сигналы векторлық қатынаспен сипатталуы мүмкін

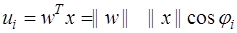. (13.24)

||w||=||x||=1 болғандықтан, u_i мәні x және w векторларының арасындағы бұрышпен анықталады, u_i=cosj_i. Сондықтан үлес векторы x ағымды оқытушы векторға ең жуық орналасқан нейрон жеңімпаз болады. Нейрон жеңісінің нәтижесінде мәндері х ағымды оқытушы вектордың мәндеріне жуықтайтын үлес коэффициенттері нақтыланады. Егер желінің кірісіне мәндері бойынша бір-біріне жуық векторлар жиынтығы берілетін болса, онда тек сол бір нейрон ғана жеңе беретін болады. Сондықтан оның үлестері бұл нейронды жеңіске жеткізіп отырған кіріс векторлары мәндерінің орташа мәніне айналады. Кезекті кіріс векторын берген уақытта жеңіске жету ғана оларға үлес коэффициенттерін нақтылап, жеңіс бар болса, оқытуды жалғастыруға мүмкіндік береді. Оқыту үдерісінің өзін-өзі ұйымдастыруы бұл сияқты бәсекелестік салдарынан болады. Нейрондар өздерінің үлестерін мәндері жағынан жуық кіріс векторларының тобын ұсынған уақытта, жеңімпаз қашанда бір нейрон болатындай нақтылайды. Қызмет етуі барысында дәл осы нейрон бәсекелестіктің арқасында кіріс мәліметтеріндегі өз санатын табады.

Әрине, біз нейрондардың барлқ модельдерін көрсеткен жоқпыз. Ең ьтанымал модельдердің ішінен Хебб моделі, инстар және оутстар Гроссберг, стохастикалық және т.б.

13.9Сигмоидальді типті бірбағытты көп қабатты желілер

Өзара біріктірілген нейрондар әріде жасанды нейрондық желілер (ЖНЖ) деп аталатын жүйені құрайды. Нейрондардың біріктірілу тәсіліне байланысты олар бірбағытты немесе рекуррентті (кері байланысы бар) желілер болуы мүмкін.

ЖНЖ танымал түрлерінің ішінен ең көп қызуғышылық тудыратыны сигмоидальді типті нейрондардан тұратын және дұрысы көп қабатты персептрон деп аталатын MLP бірбағытты көп қабатты желі. Бұл сияқты желілерде сигнал бірбағытта кірістен шығысқа қарай жүреді. Олардың математикалық сипаттаулары салыстырмалы алғанда қарапайым және айқын, ал нәтижесі алгебралық типті тура функционалды тәуелділік көрсетілуі мүмкін. Бұл сияқты желілерді оқытудың әдістеріде қарапайым және тәжірибеде жүзеге асыруда қиыншылықтар болмайды. Көп қабатты персептронды оқыту негізінен мұғаліммен бірге жүреді, ал оқытудың негізгі идеясы х- кіріс вектор, ал – оған сәйкес күтілетін желінің шығыс векторы болатын <x,d> кортеждерін таңдауда жатыр. Егер x және d векторлары өзара тең болмаса, онда желі гетероассоциативті деп аталады. Бұл сияқты типті желілерде нейрондардың персептронды модельдері немесе олардың сигмоидальді түрдегі жалпыланған формасы пайдаланылады.

13.10 Бірқабатты желілер

Бірқабатты желілерді бір жазықтықта орналасқан нейрондар құрайды (13.8-сурет). Әрбір і-ші нейронда поляризация бар (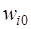 үлестерімен байланыс, бұл байланысқа сәйкес бірлік сигнал түседі), сонымен қатар, үлестерімен көптеген байланыстар бар, оларға сәйкес x_j кіріс сигналдары түседі. Үлестердің мәндері y_i шығыс сигналдарының мәндерін d_i күтілетін мәндерге жуықтатудан тұратын оқыту барысында таңдалынады. Мақсатты функция (құндық функция) жуықтық өлшемі болып саналады. М шығыс нейроны кіретін желіні оқыту үшін <x,d> оқыту векторының р санын қолданғанда, мақсатты функцияны келесі түрдегі эвклидтік метрикамен анықтауға болады

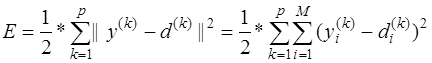. (13.25)

y_i нейронның шығыс сигналдары мәндері оқыту барысында мақсатты функцияны минимизациялау критерийі бойынша анықталатын w_ij желі үлестерінің функциясы болып табылады.

13.10-сурет. Бірқабатты сигмоидальді нейрондық желінің құрылымы

Бір деңгейде орналасқан нейрондар бір-бірінен тәуелсіз қызмет етеді, сондықтан бұл сияқты желінің мүмкіндіктері тек жекелеген нейрондардың қасиеттерімен шектеледі. Нейрондардың үлестері нақты бір шешім кеңістігін құрайды. Әрбір нейрон функционалді бейнелеуді жүзеге асыратындығын ескеру керек. f(*) сигмоидальді функция бірдеңгейлі (одноступенчатой) порогтық функцияның аналогы болып келетіндігін назарға ала отырып, нейронның шығыс сигналы (0 немесе 1 мәні) 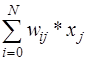өрнегінің таңбасына тәуелді болатындығын аңғаруға болады. Бұл теңдеу үлестермен салыстырмалы алғанда сызықтық болады. Үлестердің мәндері шектелген (бекітілген) мәндер болғанда y_i шығыс сигналы көп өлшемді кеңістікті екі ішкі кеңістікке бөлетін гипер жазықтықты анықтайтын х кіріс векторының орналасуына тәуелді болады. Сондықтан жіктеу тапсырмасы (нейронның шығыс сигналына 0 немесе 1мәндерін жазып қоя отыра) жалғыз нейронның ғана көмегімен шешіледі, бірақ егер нейрон сызықтық сеперация класына (мысалы, AND немесе OR логикалық функцияларын қолданылған) жататын болса ғана орындалады.

XOR екі кірісті логикалық функцияны жүзеге асыру мысалы арқылы бірқабатты желілердің мүмкіндіктерінің шектеулілігін көрсетейік. Қысқарту үшін бір сатылы түрдегі порогтың белсендендіру функциясын қолданамыз. Логикалық функцияны оқытуға берілген мәліметтер жиынтығы 18-кестеде берілген.

18-кесте. XOR функциясын оқыту үшін мәліметтер жиынтығы

x1
x2
d

Бірі 1- кіріс сигналына, ал екішісі 0-ге сәйкес болатындай етіп мәліметтер кеңістігін екі ішкі кеңістікке бөлетін жалғыз түзуді жүргізу мүмкін болмайтындығын көрсету қиындық тудырмайды (13.11-суретте штрихтелген аймақ бір класқа, ал штрихтелмеген аймақ екіші класқа тиесілі).

13.11-сурет. XOR логикалық функциясына сәйкес келетін оқыту мәліметтерін сызықтық бөлудің мүмкін еместігін көрсету

Неронның шығыс сигналы штрихтелген аймақтың ішінде 1-ге тең, ал бұл аймақтан тыста 0-ге тең болуы керек. Түзудің параметрлерінің мәндеріне (w₁₀, w₁₁, w₁₂ үлестеріне) қарамастан кеңістікті бөлуге жалғыз түзуді (бір нейронды) қолданғанда бұл сияқты шарт орындалмайды. Сонымен бір сатылы персептронның тіптен XOR сияқты қарапайым функцияның өзін жүзеге асыратындай шамасы жоқ. Бұл мәселені жасанды нейрондық желіні кеңейту жолымен оңай шешуге болады. Осы мақсатпен сатыға тағы бір нейрон қосып, екі нейронныңда үлестерін олар кеңістікті x=[x₁,x₂]^T кіріс сигналының мәніне байланысты екі кеңістікке бөліп тұратындай етіп таңдап аламыз: u₁=w₁₁*x₁+w₁₂*x₂+w₁₀>0 и u₁=w₁₁*x₁+w₁₂*x₂+w₁₀<0 (бірінші нейрон) и u₂=w₂₁*x₁+w₂₂*x₂+w₂₀>0 и u₂=w₂₁*x₁+w₂₂*x₂+w₂₀<0 (екінші нейрон). Үлестерді таңдау кеңістікті 13.12-суретте көрсетілгендей етіп бөлуді қамтамасыз етуі керек.

u₁>0, u₂>0 шарттарына сәйкес келетін ішкі жиынтықтың ортақ бөлімі u₁<0, u₂<0 шарттарына сәйкес келетін қалған аймақтан жеке аймақты анықтады.

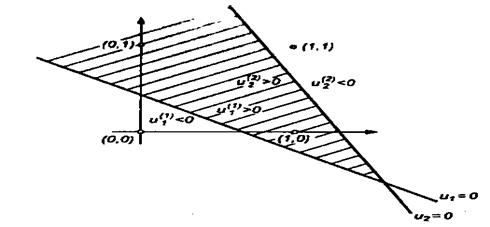
13.12-сурет. Сызықтық бөлгіштерді пайдалану жолымен сызықтық емес бөлу мәселелерін шешу

Желі шығысында жалғыз нейроннан тұратын бір қабатты қосу арқылы u₁>0, u₂>0 жиынтықтарының ортақ бөлімін ерекшелеп тұрған логикалық қосындылау функциясын жүзеге асыруға болады. XOR функциясын орындайтын нейрондық желінің ең соңғы құрылымы 13.13-суретте көрсетілген.

Желіге қосымша тағы бір қабатты қосу мәліметтерді сызықтық бөлудің мүмкіндігі жоқтығы мәселесін шешуге мүмкіндік бергенін атап өткен жөн. Жасырын қабаттың әрбір нейроны жазықтықты қосымша сызықтық бөлуді жүзеге асырады, және бұл сияқты бөлімнің u_i>0 және u_i<0 аймақтарына деген шекаралары нейрон үлесінің мәніне тәуелді болады. Шығыс қабаты жасырын қабаттың нейрондары арқылы кіріс мәліметтерінің жиынтығы бөлінген ішкі аймақтардың сәйкес комбинациясын (мысалы, логикалық қосындысын) орындайды.

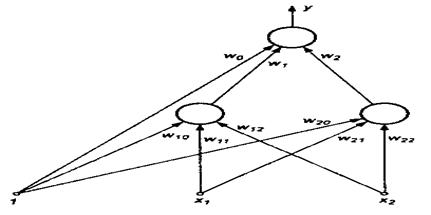
13.13-сурет. – XOR функциясын атқаратын жасанды нейрондық желінің құрылымы

Бірқабатты желілердің тәжірибелік маңызының зор болғанына қарамастан, қойылған тапсырманы орындау үшін бір қабат нейрон жеткілікті жерлерде де оны қолдануды жалғастырып келеді. (Несмотря на то, что однослойная сеть имеет небольшое практическое значение, ее продолжают использовать там, где для решения поставленной задачи достаточно и одного слоя нейронов.)

Желінің бұл сияқты архитектурасын таңдап алудың себебі өте қарапайым. Кіріс нейрондарының саны x кіріс векторының өлшемімен, ал шығыс нейрондарының саны d векторының өлшемімен анықталады. Желіні оқыту мұғаліммен бірге жүргізіледі және оқытуды жүргізу барысы тура бірлік нейронды оқытудың көшірмесі сияқты.

13.11 Көп қабатты персептрон

Көп қабатты желі әртүрлі сатыларда орналасқан нейрондардан тұрады, сонымен қатар кіріс және шығыс қабаттардан басқа жоқ дегенде бір ішкі, яғни жасырын қабат болады. Нейрондық желілер саласына арналған әдебиеттерде көрсетілгендей бұл сияқты нейрондық жүйе көп қабатты персептрон деп аталады. Суретте жасырын бір қабаты бар желі берілген.

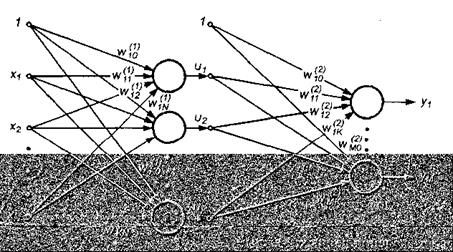
13.14-сурет. Екі қабатты сигмоидальді нейрондық желінің жалпылама құрылымы (бір жасырын қабаты бар)

Төменде берілетін келесі талқылаулардың барлығыда осы сияқты желілерге қатысты. Үлестердің сигналдарының белгілеулері де суретке сәйкес болады. Жасырын қабаттың нейрондарының үлесін жоғарғы индекспен (1), ал шығыс қабатының нейрондарының үлесін жоғарғы индекспен (2) белгілейміз. Жасырын қабаттың нейрондарының шығыс сигналдарын 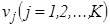, ал шығыс қабатының нейрондарының шығыс сигналдарын белгілейміз. Нейрондарды белсендендіру функциясы униполярлы немесе биполярлы сигмоидальді формада берілген делік. Сипаттауды қысқарту үшін желінің кіріс векторының кеңейтілген белгілеуін 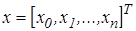түрде қолданамыз, мұнда, поляризацияның бірлік векторына сәйкес келеді. Х векторымен желінің екі кіріс векторы байланысқан: y 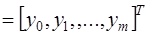фактілік шығыс сигналдарының векторы, ал d күтілетін шығыс сигналдарының векторы.

Оқытудың мақсаты желінің барлық қабаттарының және 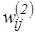үлестерінің мәндерін х кіріс векторы берілген уақытта үшін күтілетін мәндерімен қажетті дәлдікпен сәйкес болатын шығыста сигналдарының мәнін алуға болатындай етіп таңдау. Егер бірлік поляризациялық сигналды Х кіріс векторының бір компоненті ретінде қарастыратын болсақ, онда поляризация үлестерін екі қабаттың да сәйкес нейрондарының үлес векторларына қосуға болады. бұл сияқты жағдайда жасырын қабаттың і-ші нейронының шығыс сигналын төмендегі функциямен сипаттауға болады

, (13.27)

Мұндағы 0 индексі сигналға және поляризация үлесіне сәйкес болады және 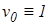, 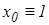. Шығыс қабатындағы к-ші нейрон төмендегі функциямен анықталатын шығыс сигналын туындатады

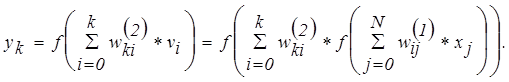(13.28)

Соңғы формуладан шығатыны: шығыс сигналының мәні екі қабаттың да үлесіне әсер етеді, ал бұл уақытта жасырын қабатта туындайтын сигналдар шығыс қабатының үлесіне тәуелді емес.

13.12 Қатенің кері таралу (распространения) алгоритмі

Бұл алгоритм тиімдеудің градиенттік әдістерін қолдана отырып көп қабатты желінің үлестерін таңдау стратегиясын анықтайды. Осы уақытта бұл алгоритм көп қабатты желіні оқытудың ең нәтижелі алгоритмдерінің бірі болып саналады. Оның негізін шығыс сигналдарының фактілік мәндерімен күтілетін мәндерінің арасындағы айырманың квадраттарының қосындысы түрінде құрылатын мақсатты функция құрайды. (x,d) бірлік оқытатын таңдау жағдайында мақсатты функция келесі түрде анықталады

(13.29)

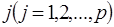оқытатын таңдаулар саны көп болғанда, мақсатты функция барлық таңдаулар бойынша қосындыға айналады

(13.30)

Үлестерді нақтылау әрбір оқытатын таңдауды ұсынғаннан кейін («онлайн» режимі деп аталатын) жүргізіледі немесе оқыту циклін құрайтын барлық таңдауларды ұсынғаннан кейін («оффлайн» режимі) бір рет жүргізіледі. Ұсынылған материалда әрі қарай әрбір таңдаудан кейін үлестерді белсендендіруге сәйкес келетін мақсатты функция (бірінші формула) пайдаланылады.

Қысқарту үшін оқытудың мақсаты желінің әрбір қабатының нейрондарының үлестерінің мәндерін кіріс векторы берілген уақытта үшін күтілетін мәндерімен қажетті дәлдікпен сәйкес болатын шығыста сигналдарының мәнін алуға болатындай етіп анықтау деп санауға болады.

Қателерді кері тарату алгоритмін қолдана отырып желіні оқыту бірнеше кезеңмен жүргізіледі. Олардың біріншісінде х оқытатын таңдауы ұсынылып, желінің сәйкес нейрондарының сигналдарының мәні есептелінеді. х векторының берілген уақытта бірінші жасырын қабаттың шығыс сигналының мәні, одан кейін шығыс қабатының нейронының мәні анықталады. Есептеу жүргізу үшін жоғарыда көрсетілген формулалар қолданылады. шығыс сигналдарының мәндері алынғаннан кейін 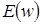мақсатты функциясының нақты мәнін есептеу мүмкін болады. Екінші кезеңде бұл функцияның мәні минимизацияланады.

Егер мақсатты функцияны үзіліссіз деп санасақ, онда оқытудың ең нәтижелі тәсілдері болып тиімдеудің градиенттік әдістері болып табылады. Оларға сәйкес үлестер векторын (оқыту) нақтылау 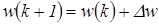формуласымен жүргізіледі, мұндағы 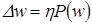, η – оқыту коэффициенті, ал P(w) – w көп өлшемді кеңістіктегі бағыт.

Градиентті әдістерді қолдана отырып көп қабатты желіні оқыту желінің барлық қабаттарының үлестеріне қатысты градиент векторын анықтауды қажет етеді, ал бұл P(w) бағытын дұрыс таңдау үшін керек. Бұл тапсырманың тек шығыс қабаттарының үлестері үшін ғана анық шешімі бар. Басқа қабаттар үшін жасанды нейрондық желілер теориясында қателіктерді кері тарату алгоритмі (англ. Error backpropagation) деп аталатын арнайы стратегия жасалған, бұл алгоритм болса желіні оқыту процедурасымен теңестіріледі. Бұл алгоритмге сәйкес оқытудың әрбір циклінде келесі кезеңдер анықталады.

Кезекті х векторын құрайтын кіріс сигналдарын генерациялауда ақпаратты тура бағытта жіберудегі нейрондық желіні талдау. Мұндай талдаудың нәтижесінде жасырын қабаттың және шығыс қабатының нейрондарының шығыс сигналдарының мәні, сонымен қатар әрбір қабаттың белсендендіру функцияларының 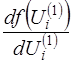, ,…, сәйкес туындылары есептелінеді (m- желі қабаттарының саны).

Сигналдарды жіберу бағытын өзгерту, белсендендіру функциясын олардың туындыларымен алмастыру және еліктіру желісінің бұрынғы шығысына (қазіргі уақыттағы кірісі) фактілік және күтілетін мәндердің айырмасы түрінде жіберу арқылы қателіктерді кері тарату желісін құру. Бұл сияқты жолмен анықталған желі үшін қажетті кері айырмаларды (обратных разностей) есептеу керек.

Үлестерді нақтылау (желіні оқыту) жоғарыда ұсынылған формулалар бойынша оргинал желі және қателіктерді кері тарату желісі үшін 1 және 2 п. алынған нәтижелер негізінде жүргізіледі.

1 және 3 п. сипатталған үдерістерді барлық оқытатын таңдаулар үшін алгоритмді тоқтату шарты орындалғанға дейін жалғастыра беру керек. Градиент нормасы оқыту үдерісінің дәлдігін сипаттайтын ε априори мәнінен төмендегенде алгоритм әрекеті тоқтатылады.

Нейрондық желі теориясы үшін нейрондық желілердің нақты типтеріне арналған базалық формулалармен олардың өзгертулері классикалық деп саналады. Осы себепті біз тек бір жасырын қабаты бар желіге қатысты шарттарды ғана қарастырамыз. Используемые обозначения представлены на рис. N.

Бұрынғы сияқты кіріс түйіндерініңі санын N әріпімен, жасырын қабаттағы нейрондар санын – K, ал шығыс қабаттағы нейрондар санын - M деп белгілейміз. Бұл нейрондардың сигмоидальдік белсендендіру функциясын қолданамыз. Алгоритмнің негізін мақсатты функцияны желінің шығыс сигналдарының фактілік мәндерімен күтілетін мәндерінің арасындағы айырманың квадраттарының қосындысы түрінде есептеу құрайды. бірлік (x,d) оқытатын таңдау жағдайында мақсатты функция және оқытатын таңдаулардың жиынтығы Е формуласымен беріледі. Баяндалып отырған материалды қысқарту үшін әрбір оқытатын таңдауды ұсынғаннан кейін үлестерді нақтылауға мүмкіндік беретін мақсатты функцияны қолданамыз.

N-суретте берілген белгілеулерді ескере отырып, бұл функция келесі өрнекпен анықталады

С учетом обозначений, введенных на рис. N, эта функция определяется выражением

.

(13.31)

Градиенттің нақты компоненттері бұл өрнекті дифференциалдау арқылы есептелінеді. Бірінші кезекте шығыс қабатының нейрондарының үлестері анықталады. Шығыс үлестері үшін аламыз:

,

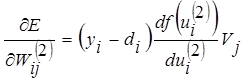(13.32)

мұнда .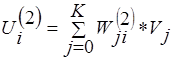

Егер 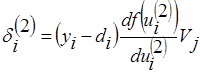белгілеуін енгізетін болсақ, онда шығыс қабаты нейрондарының үлестеріне қатысты градиенттің сәйкес компонентін төмендегі түрде көрсетуге болады

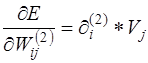. (13.33)

Жасырын қабаттың нейрондарына қатысты градиенттің компоненттері осы қағида бойынша анықталады, бірақ олар төменде берілген түрдегі функцияның (13.34) бар болуынан туындайтын күрделі тәуелділікпен сипатталады

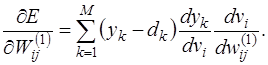(13.34)

Бұл өрнектің жекелеген құрауыштарын (составляющих) нақтылағаннан кейін аламыз:

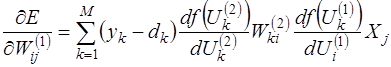(13.35)

Егер төмендегі белгілеуді енгізетін болсақ

, (13.36)

онда жасырын қабаттың нейрондарының үлестеріне қатысты градииеттің компоненттерін анықтайтын өрнекті аламыз

. (13,37)

Екі жағжайда да 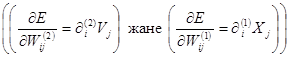градиенттің сиппаттамасының құрылымы бірдей және екі сигналдың көбейтіндісімен беріледі: біріншісі бұл безбенделген (салмақталған, ойластырылған, взвешенный) байланыстың бастапқы түйініне сәйкес келеді, ал екіншісі бұл байланыс орнатылған түйінге ауысқан қателікке сәйкес келеді. Градиент векторын анықтау келесі үлестерді анықтау үдерісі үшін аса маңызды. Қатені кері таратудың классикалық алгоритмінде P(W) факторы теріс градиенттің бағытын көрсетеді, сондықтан

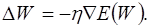(13.38)

Бағытты таңдаудың мұнанда тиімді әдістері бар.

Дата добавления: 2015-06-04