Потік магнітного поля. Теорема Гауса для магнітного поля в вакуумі

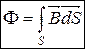Ф]=1 Вб =1 Тл×м²= 1 Н×м²/А×м= 1 В×с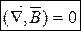

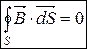
Теорема про циркуляцію магнітного поля в вакуумі

Циркуляція вектора :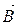

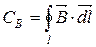
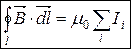
Обчислення магнітних полів за допомогою теореми про циркуляцію

1) М.п. прямолінійного провідника R нескінченної довжини з струмом I.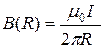

2) Магнітне поле нескінченно довгого соленоїда 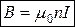n×I - кількість ампер-витків.

3) Магнітне поле тороїда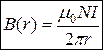

Локальна форма теореми про циркуляцію

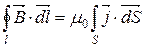За теоремою Стокса: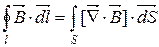

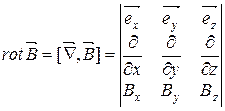
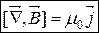
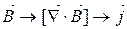
Потенціальні та вихрові поля

	Електростатичне поле	Магнітне поле
Силова характеристика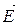
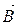
Теорема Гауса в інтегральній формі		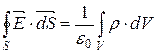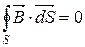поле соленоїдне
Теорема Гауса в локальній формі		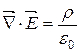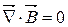поле бездівергентне
Теорема про циркуляцію	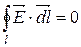поле потенціальне
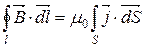
Теорема про циркуляцію в локальній формі		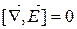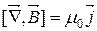вихрове поле

Магнітне поле в речовині. Магнетики.

Маг. момент атомів та молекул. Намагн.. Вектор .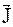

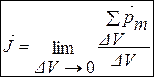
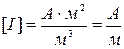
Струми намагнічування. Т. Гауса для магнітного поля в речовині.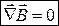

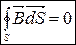
Т. про циркуляцію маг. поля в речовині. Вектор напруженості магнітного поля Н.

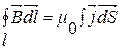
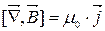
У вакуумі: 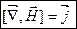В речовині: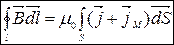

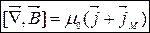
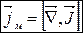
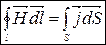
Магнітна сприйнятливість. Магнітна проникність речовини.

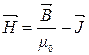
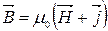
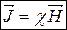
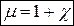
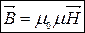
Умови на межі поділу двох магнетиків.

1 Умови для нормальних складових .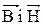

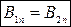
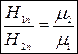
2 Умови для тангенціальних складових 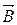i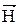

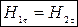
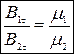
3. Заломлення ліній вектора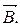

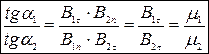
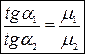
Магнетики.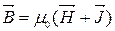

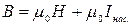
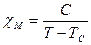
Електромагнітна індукція.

Спостереження та експериментальні закономірності явища.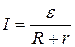

Основний закон електромагнітної індукції.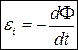

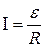
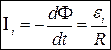
Явище самоіндукції. Індуктивність контуру.

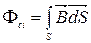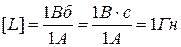
І=І(t) 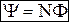потокозчеплення

Струм при замиканні та розмиканні електричного кола з індуктивністю.

1 Розмикання 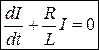кола. 2 Замикання кола.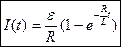

Взаємна індукція.

Енергія магнітного поля.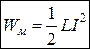

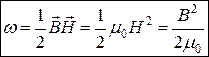
Природа електромагнітної індукції.

1. Виникнення ЕРС самоіндукції в провіднику, що рухається.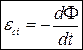

2. Вихрове електричне поле.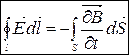

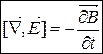
Рівняння Максвела

Струм зміщення

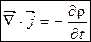
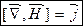
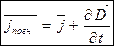
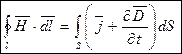
Система рівнянь Максвела

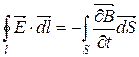
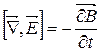
1)		Закон електромагнітної індукції
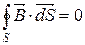
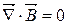
2)		Теорема Гауса для магнітного поля
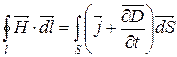
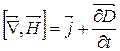
3)		показує. що змінне електричне поле утворює у просторі змінне магнітне поле
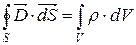
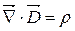
4)		Теорема Гауса для електричного поля

Матеріальні співвідношення: .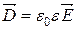

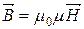
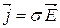Диф. с-му рівнянь доповнюють граничними умовами:D_2n=D_1n E_2t=E_1t B_2n=B_1n H_2t=H_1t

Надамо заряд відокремленому провіднику.

q® φ 2q ® 2φ φ ~ q 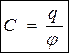(3.3)

Електроємність відокремленого провідника – відношення q до φ, показує який заряд q треба надати провіднику, щоб збільшити потенціал на одиницю. Характеризує здатність провідника до накопичування зарядів.

Приклад: обчислити С кулі з радіусом R, діелектричною проникністю ε.

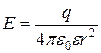
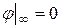
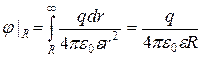
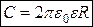(3.4)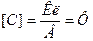

Ємність 1 фарад – ємність такого провідника, при наданні заряду в 1 кулон потенціал якого змінюється на 1 вольт. Ємність провідної кулі з розмірами Землі: R_з=6400 км С_з=0,7 мФ

Ємність конденсатора

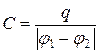
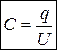(3.5)

Ємність конденсатора визначається його геометрією (форма, розмір обкладок, зазор між обкладками) та діелектричними характеристиками середовища.

Алгоритм розв’язку задач:

1) За теоремою Гауса знаходять Е в просторі між обкладками.

2) Обчислюють напругу: 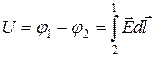3) Обчислюють С: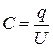

Приклади

1.Плоский конденсатор

d, S,ε

C-?

:

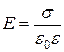
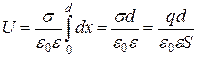
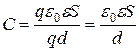
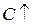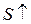
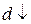
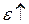
2.Циліндричний 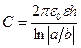3.Сферичний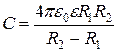

Дата добавления: 2015-06-04