
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Плотность энергии магнитного поля
|
|
|
|
Индуктивность тороида
Если в тороиде протекает ток I, то внутри него создается магнитное поле, индукция которого определяется формулой (17.32). Магнитный поток через один виток – BS, а через N витков
 ,
,
где S – площадь сечения тороида.
Подставив сюда значение B из (17.32), получим
 ,
,
т.е. индуктивность тороида
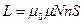 ,
,
Поскольку N=nl, где l – длина осевой линии тороида, то
 . .
| (18.14) |
где V = lS – объем тороида.
Формулу (18.14) можно использовать также для вычисления индуктивности соленоида при условии, что его длина значительно больше диаметра: l>>d.
Соединим параллельно с источником тока индуктивность L и сопротивление R (рис. 18.4). При выключении источника в верхней части цепи, содержащей индуктивность и сопротивление, некоторое время будет идти ток, который поддерживается ЭДС самоиндукции. Элементарная работа ЭДС самоиндукции
 ,
,
а полная работа
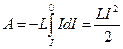 ,
,
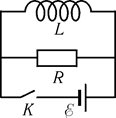 Рис. 18.4
Рис. 18.4
|
Выполнение этой работы сопровождалось исчезновением магнитного поля внутри соленоида. На основании закона сохранения энергии можно заключить, что работа A производилась за счет энергии магнитного поля W:
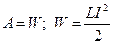 . .
| (18.15) |
Выразим энергию (18.15) через характеристики магнитного поля соленоида. Для этого подставим в (18.15) выражение для индуктивности соленоида (18.14) и значение силы тока I из (17.32). Имеем
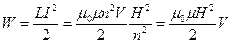 , ,
| (18.16) |
где V — объем соленоида.
Ранее было показано, что магнитное поле соленоида сосредоточено в его объеме. Введем понятие плотности энергии магнитного поля, т.е. энергии, сосредоточенной в единичном объеме поля:
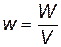 [Дж/м3]. [Дж/м3].
| (18.17) |
Из (18.16) и (18.17) следует, что плотность энергии магнитного поля
 . .
| (18.18) |
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 590; Нарушение авторских прав?; Мы поможем в написании вашей работы!