Фазовая и групповая скорости света

Рассмотрим плоскую монохроматическую волну 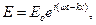где k = 2p/l — волновое число.

Зафиксируем некоторое значение фазы волны:

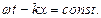
(28.1)

Скорость, с которой перемещается в пространстве данное значение фазы, называется фазовой скоростью. Поскольку 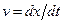, то из выражения (28.1) следует, что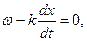

т.е. фазовая скорость

(28.2)

В реальных условиях под монохроматической волной понимается со­вокупность волн с частотами, заключенными в более или менее узком интервале ширинойDw. Суперпозиция таких волн, мало отличающихся друг от друга по частоте, называется группой волн. В результате наложения волн с близкими частотами возникают биения (см. § 21.8). Точка, в которой амплитуда (а значит, и интенсив­ность) группы волн имеет максимум, называется центром группы волн. Центр группы волн перемещается со скоростью, которая называется — групповой.

Рассмотрим для простоты группу волн, состоящую из двух монохро­матических волн с близкими частотами w иw+Dw:

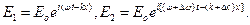
Результирующая волнаE=E1+E2 описывается уравнением

.

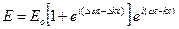Первый множитель, стоящий в квадратных скобках, изменяется гораздо медленнее,чем второй, поэтому его можно рассматривать как ампли­туду. Максимальное значение амплитуды достигается, если

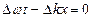
Отсюда для групповой скорости получаем

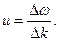
или

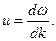
(28.3)

Найдем связь между групповой и фазовой скоростью. Так как w=2pn, то

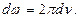
(28.4)

Далее имеем 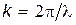, а так как 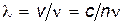, где n — показатель преломления, то

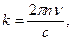
откуда

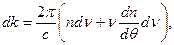
(28.5)

Подставляя (28.4) и (28.5) в (28.3), окончательно получаем:

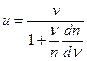
(28.6)

Из (28.6) видно, что групповая и фазовая скорости совпадают лишь в том случае, когда dn/dn, т.е. показатель преломления n не за­висит от частоты световой волны. В общем случае u¹v, поскольку n=n(n).

Круг явлений, в которых наблюдается зависимость показателя пре­ломления n от частоты n, называется дисперсией.

Дата добавления: 2015-06-04