Поглощение света. Элементарная классическая теория дисперсии

Элементарная классическая теория дисперсии

Используя выражение (24.13), устанавливаем связь между показате­лем преломления среды и диэлектрической проницаемостью:

Поскольку e=1+æ (см. формулу (12.16)), гдеæ — диэлект­рическая восприимчивость вещества, то

(28.7)

Таким образом, для нахождения функции n=n(n).необходимо найти зависимость æ от частоты n.

Так как световые волны обладают очень высокой частотой (n~ 10¹⁵Гц), то их действие на атомы вещества сводится к смещению электронов в электрическом поле световой волны и появлению деформа­ционной поляризации.

Рассмотрим простейший случай, когда атом имеет лишь один элект­рон. Под действием световой волны

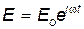
(28.8)

электрон совершает вынужденные колебания, уравнение которых (см. § 21.12):

где амплитудное значение силы, действующей на электрон се стороны электрической составляющей световой волны,

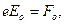
(28.9)

m —масса электрона.

Электрон смещается от положения равновесия на величину x в результате чего атом приобретает наведенный дипольный момент pe=ex. Пусть no — число атомов в единице объема вещества. Тогда поляризованность

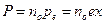
(28.10)

Однако поляризованность связана с напряженностью электрического поля соотношением (12.10). Сравнивая (28.10) и (12.10), находим ди­электрическую восприимчивость

Подставим в это выражение величину смещения x из (21.48)и значениеE из (28.8). После сокращения на e^iwt получим

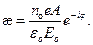
(28.11)

где A— амплитуда; j — начальная фаза вынужденных колебаний электрона.

Используя формулу Эйлера (cм. Математическую справку), найдем действительную часть выражения (28.11):

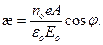
Таким образом,

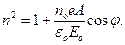
(28.12)

Воспользовавшись известным тригонометрическим тождеством

и учтя (21.51), получим

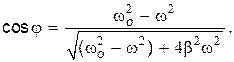
(28.13)

Подставляя (28.13) и (21.50) в (28.12) и учитывая (28.9),по­лучаем

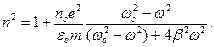
(28.14)

Если затухание отсутствует (b= 0), то

(28.15)

Из выражения (28.15) видно, что в области частот w<w_o при w®w_o n²®¥, а в области частот w>w_o при w®w_o n²® –¥ (рис.28.1,а).

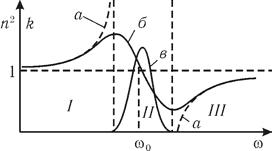Рис. 28.1

Физически бессмысленные бесконечные значения n² при w=w_o получены из-за нашего предположения об отсутствии затухания. На самом деле b¹0 и функция n²(w) ограниченна и не­прерывна. График зависимости n²(w) при b¹0 показан на рис. 28.1, б. В области частот I и Ш показатель преломления уве­личивается с ростом частоты. Это области нормальной дисперсии. Вблизи от частоты собственных колебаний электрона w_о — область II показа­тель преломления резко уменьшается с ростом частоты световых воли — это область аномальной дисперсии. Поскольку на частотах, близких к w_о, вещество поглощает свет (см. § 28.3), то область аномальной дисперсии совпадает с полосой собственного поглощения ве­щества.

Поглощение света носит резонансный характер, т.е. из всего спектра волн, падающих на вещество, избирательно поглощаются такие волны, частоты которых соответствуют собственным частотам колебаний электронов в атомах. При этом энергия волн превращается в энергию колебательного движения электронов.

Выделим в веществе бесконечно тонкий слой толщинойdx, на который падает свет интенсивностью I. После прохождения этого слоя интенсивность света убывает на некоторую величину – dI:

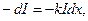
(28.16)

где k — коэффициент поглощения, зависящий от частоты световой волны и рода вещества.

Разделяя переменные в (28.17) и интегрируя, получаем

(28.17)

где Io — начальное значение интенсивности.

Соотношение (28.17) носит название закона Бугера.

В классической электродинамике доказывается, что коэффициент поглощения k численно равен модулю мнимой части диэлектрической восприимчивости æ формула (28.11):

(28.18)

Используя (21.51), с помощью тригонометрического тождества

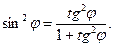
можно получить

(28.19)

Подставим (28.19) и (21.50) в (28.18). С учетом (28.9) получим выражение, описывающее зависимость коэффициента поглощения от частоты световой волны:

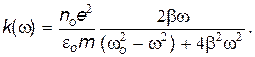
(28.20)

Из (28.20) видно, что при w®0 или w®¥ коэффици­ент поглощения k(w), т.е. световые волны с очень малыми или очень большими частотами практически не поглощаются веществом. Максимум поглощения наблюдается вблизи частоты собственных колебаний электрона в атоме w_o»w_o, (рис. 28.1, в).

Явление поглощения света (с использованием закона Бугера) применяется для количественного и качественного анализа веществ.

Дата добавления: 2015-06-04