Предмет, основные понятия статики

Основные понятия и аксиомы статики.

• Предмет, основные понятия статики.
• Аксиомы статики.
• Первая аксиома.
• Вторая аксиома.
• Третья аксиома.
• Четвертая аксиома.
• Пятая аксиома.
• Шестая аксиома.

В статике в соответствие с моделями теоретической механики изучают равновесие материальных точек, твердых тел и их систем. Наибольший интерес представляет равновесие твердого тела и систем твердых тел. Поэтому в статике мы будем изучать статику твердого тела и систем твердых тел.

Статика - это раздел теоретической механики, в котором изучают равновесие тел под действием сил и преобразования систем сил.

Для статики и динамики одним из основных понятий является понятие силы. Состояние равновесия или движения тела зависит от его взаимодействия с другими телами. Меру этого взаимодействия в механике называют силой.

Из определения силы следует, что источником силы является только тело, а во взаимодействии могут находиться, как минимум, два тела. Силы могут возникать как при непосредственном контакте тел, так и при взаимодействии на расстоянии, например, силы всемирного тяготения.

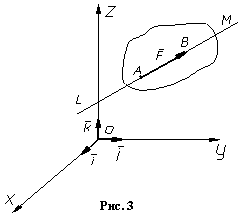
Действие силы на реальное физическое тело, которое деформируется силой, определяется: 1) величиной или модулем силы; 2) направлением силы; 3) точкой приложения силы. То есть сила, приложенная к физическому телу, является связанным вектором, который нельзя перемещать внутри физического тела. Само же физическое тело и вместе с ним сила могут перемещаться в пространстве. На рис. 3 показана сила, приложенная в точке A. Длина отрезка AB в определенном масштабе равна модулю силы. Точка B называется концом вектора силы. Стрелка на конце вектора указывает направление силы. Прямая LM, на которой лежит вектор силы, называется линией действия силы.

Модуль силы находят сравнением с силой, принятой за единицу измерения. Основной единицей силы в Международной системе единиц является 1 ньютон (1 Н). Для измерения силы служат приборы, называемые динамометрами, в которых измеряемую силу сравнивают с линейной силой упругости, а величину силы определяют по деформации упругих элементов динамометров - пружин, торсионов и т.д.

Из математики известно, что связанные векторы определяются шестью независимыми параметрами. Скользящие векторы, которые можно переносить вдоль линии действия, определяются пятью параметрами, а свободные векторы, которые можно переносить параллельно самим себе в любую точку пространства, - тремя параметрами. Силу, как связанный вектор, удобнее определить в системе отсчета OXYZ (рис. 3) следующими параметрами. Это координаты точки приложения XA, YA, ZA и проекции силы на оси координат Fx, Fy, Fz. Первые три параметра определяют точку приложения силы A, а остальные три определяют величину и направление силы:

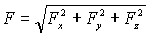
	(1)
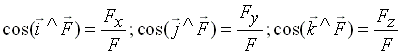
	(2)

В выражении (2) представлены косинусы углов между осями координат и силой, которые называются направляющими косинусами и определяют направление силы в пространстве.

Далее физическое тело будем называть телом, а состояние движения или равновесия тела под действием сил будем называть состоянием.

Введем понятие системы сил. Системой сил назовем совокупность сил 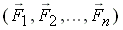, действующих на одно тело.

Так как силы, приложенные к телу и к твердому телу, не являются свободными векторами, то для систем сил используется понятие эквивалентности систем сил. Системы сил эквивалентны друг другу, если при замене одной системы сил 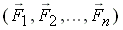на другую 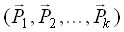состояние тела не изменится. Математическая запись этого утверждения .

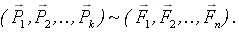Система сил является уравновешенной или эквивалентной нулю, если под ее действием тело находится в равновесии и тогда 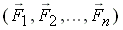~ 0.

В равновесии или покое все точки тела не перемещаются относительно системы отсчета. Точное определение равновесия будет сформулировано при изучении динамики. Если система отсчета движется, то равновесие называется относительным. Если система отсчета близка к неподвижной, то равновесие называют абсолютным или просто равновесием. При решении задач статики за неподвижную можно принять систему отсчета, оси которой связаны с поверхностью Земли.

В том случае, когда система сил 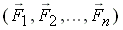эквивалентна одной силе , последняя называется равнодействующей.

В заключение пункта рассмотрим классификацию систем сил. Если на положение сил системы нет ограничений и силы произвольно расположены в пространстве, то систему сил называют произвольной или пространственной. Если силы системы лежат в одной плоскости, то систему сил называют плоской. Силы, линии действия которых пересекаются в одной точке, называются сходящимися, а силы, линии действия которых параллельны друг другу называют параллельными. Соответственно существуют пространственные и плоские системы сходящихся и параллельных сил.

Дата добавления: 2015-06-04