Пример 1. Связи и реакции связей

Несвободное тело можно рассматривать как свободное, заменив связи их реакциями.

Две основные задачи статики.

1. Задача о приведении системы сил: заключается в замене данной стстемы сил другой, наиболее простой, ей эквивалентной.

2. Задача о равновесии состоит в определении условий, при которых система сил приложенная к телу будетуравновешенной системой.

Принцип освобождаемости от связей широко используется и в динамике для исследования движения несвободных тел. Поэтому важно уметь правильно заменять отброшенные связи их реакциями, что является одним из важных этапов решения задач статики и динамики. Существуют основные правила построения реакций связей.

1. При непосредственном контакте тела и связи, если контакт происходит в одной точке, то реакция связи приложена в точке контакта. Если контакт происходит по площади, то реакция приложена в центре приведения распределенных сил, например в центре давления, для выталкивающей или архимедовой силы.

2. Реакция связи приложена к телу, а не к связи.

3. Реакция связи направлена в сторону противоположную той, куда связь не дает перемещаться телу.

Рассмотрим некоторые виды связей.

Идеально гладкие поверхности. Таких поверхностей в природе нет. В инженерной практике за идеально гладкую поверхность можно принять поверхность, у которой поверхностная сила трения значительно меньше других сил, например, поверхность льда.

На рис. 9, a изображено твердое тело на идеально гладкой поверхности. Реакция связи возникает в точке контакта тела со связью и приложена к телу. Связь позволяет телу скользить по ее поверхности, и оторваться от нее. Она не позволяет телу перемещаться по нормали к поверхности связи во внутрь связи. Следовательно реакция идеально гладкой поверхности направлена по нормали к поверхности в сторону от связи. Далее используем аксиому связей. В результате перейдем от несвободного тела к свободному, к которому приложена сила, заменившая идеально гладкую поверхность.

На рис. 9, b показан грузик на идеально гладкой наклонной плоскости. Контакт тела и связи происходит по плоскости и силы взаимодействия распределены по площади. Они приводятся к одной силе, приложенной в геометрическом центре площади. Проведя аналогичные рассуждения, применим принцип освобождаемости от связей. Отбросив наклонную плоскость, заменив ее силой N, изобразим грузик как свободное тело. Этот рисунок называется расчетной или силовой схемой.

Однородный брус веса P положен в выемку, как показано на рис. 9, c, и находится в равновесии. Требуется расставить активные силы, реакции связей и получить расчетную схему задачи.

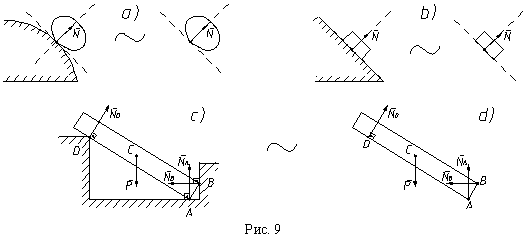Активной силой является вес бруса. Из физики известно, что для однородных тел точкой приложения веса является геометрический центр бруса - точка C. В точках A и B реакции направлены по нормали к поверхности выемки в сторону от связи. В точке D имеет место опора на острие. К острию нельзя построить касательную, а следовательно, и нормаль. Поэтому мы вынуждены использовать правила построения реакций связей. Реакция связи приложена в точке контакта. Определяем, куда острие D не дает перемещаться брусу. Брус может скользить по острию и оторваться от острия. Он не может перемещаться только внутрь связи в направлении по нормали к поверхности бруса. Следовательно, реакция острия направлена от острия по нормали к поверхности тела (в нашем случае - бруса). Заменим связь (выемку) ее реакциями - тремя силами N_A, N_B, N_D, затем ее отбросим. В результате получим расчетную схему (рис. 9, d), где брус изображен как свободное тело, которое согласно аксиоме связей, попрежнему находится в равновесии под действием активной силы и реакций связи.

У реакций связей, изображенных на рис. 9, известны точка приложения и направление. Величина этих реакций вычисляется при решении конкретной задачи.

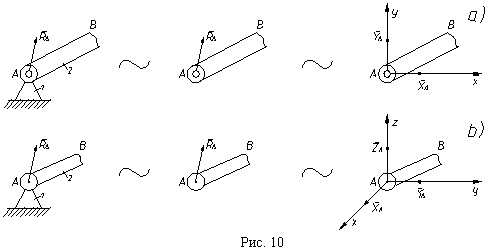Существуют связи, у реакций которых известна только точка приложения. Остальные параметры вычисляются при решении задач. К таким связям относятся неподвижные цилиндрический (рис. 10, a) и сферический (рис. 10, b) шарниры. Эти шарниры соединяют тела так, что одно тело может поворачиваться относительно другого.

Цилиндрический шарнир допускает вращение вокруг одной оси, называемой осью шарнира, которая проходит через точку A. Образцами цилиндрического шарнира являются соединение двух половин ножниц, шарниры двери и т.д. Цилиндрический шарнир не дает перемещаться концу A тела AB в любом направлении в плоскости, перпендикулярной оси шарнира. Следовательно, реакция шарнира может занимать в этой плоскости любое положение, известна лишь точка приложения - A. При решении задач аналитическими методами эту одну реакцию R_A удобно представить как равнодействующую двух неизвестных составляющих X_A, Y_A, которые направляют параллельно осям координат, как показано на рис. 10, a. Физически это отражает то, что неподвижный шарнир не дает перемещаться концу A тела AB вдоль осей координат, в нашем случае вправо-влево, вверх-вниз.

Сферический шарнир позволяет поворачиваться телу вокруг любой оси, проходящей через точку A. Однако он не дает перемещаться концу A тела AB в пространстве. Следовательно, реакция шарнира может занимать в пространстве любое положение, известно лишь, что она проходит через точку A. При решении задач аналитическими методами эту реакцию представляют тремя составляющими X_A, Y_A, Z_A. Это означает, что сферический шарнир не дает перемещаться концу A вдоль трех осей координат, в нашем случае (рис. 10, b) вперед-назад, вправо-влево, вверх-вниз.

Сформулированные аксиомы являются фундаментом, на котором строится статика. Кроме того, аксиома действия и противодействия и аксиома связей используются в динамике при изучении движения несвободных материальной точки и твердого тела.

Дата добавления: 2015-06-04