Основные понятия. Теорема о трех силах

Вопрос

Будем рассматривать абсолютно твердое тело, т.е. такое тело, расстояния между двумя любыми точками которого остаются неизменными. Это значит, что мы отвлекаемся от деформаций, возникающих всегда при действии силы на любое реальное тело*).

Далее, мы не будем различать состояние равномерного прямолинейного движения и покоя, т.е. будем всегда выбирать для рассмотрения ту инерциальную систему отсчета, где тела покоятся. Чтобы исключить возможность свободного вращения тела по инерции, вообще говоря, не противоречащую условиям равновесия, мы будем предполагать, что во всех утверждениях, касающихся силового воздействия на тело, воздействие это оказывается на тело, первоначально находившееся в покое.

Будем говорить, что система сил {s} (приложенных к абсолютно твердому телу) находится в равновесии или эквивалентна нулю, если данная система не сообщает телу никакого движения, и записывать это следующим образом: {s} {0}.

1. Аксиомы статики. Существенной характеристикой силы в этих аксиомах помимо величины и направления выступает положение точки ее приложения.

Рис. 1

1. Система двух сил находится в равновесии тогда и только тогда, когда эти силы равны по величине, противоположны по направлению и точки их приложения лежат на линии действия сил (эти точки могут и совпадать), (рис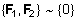. 1):

. (1)

2. Две системы сил, различающиеся на систему, эквивалентную нулю, эквивалентны между собой:

{s} {s} + {o}, (2)

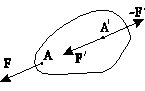Рис. 2

т.е. к любой системе сил можно прибавлять (или отнимать от нее) без изменения ее действия приложенную произвольным образом систему сил, эквивалентную нулю.

Следствие аксиом 1 и 2. Сила (приложенная к абсолютно твердому телу) — вектор скользящий, т.е. точку ее приложения можно произвольно перемещать вдоль линии ее действия.

Для доказательства выберем на линии действия силы F, приложенной в точке А (рис.2), произвольную точку А и приложим в ней (эквивалентную нулю) систему двух сил { F, - F }, равных по величине F. Но силы F и - F образуют эквивалентную нулю систему ({ F, - F } 0), которую можно отбросить. Таким образом, останется лишь сила F, равная F, но приложенная в другой точке.

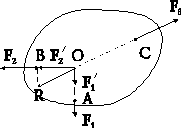  Рис. 3

3. Система двух непараллельных сил, приложенных в одной точке, эквивалентна одной силе (равнодействующей), приложенной в той же точке и определяемой по правилу параллелограмма (содержание этой аксиомы выражает основное свойство сил, приведенное в лекции 2).

2. Теорема о трех силах. Если (абсолютно твердое) тело находится в равновесии под действием плоской системы трех непараллельных сил (т.е. сил, из которых хотя бы две непараллельные), то линии их действия пересекаются в одной точке.

Доказательство. Пусть из трех сил F 1, F 2, F ₃, приложенных соответственно в точках А, В и С (рис.3), непараллельными являются F 1и F 2. Продолжим линии их действия до пересечения в точке О и перенесем в эту точку обе силы. Очевидно, система { F 1, F 2} эквивалентна 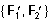, а эта последняя уже имеет равнодействующую R. Таким образом,

{ F 1, F 2, F 3} { R, F 3,}. (3)

Но система двух сил находится в равновесии только в том случае, если они направлены вдоль одной прямой. Следовательно, линия действия F 3должна совпасть с линией действия R, т.е. пройти через точку О.

  Рис. 4

Замечание. Доказанное усло­вие является необходимым, но не достаточным условием равновесия. Для достаточности нужно еще равенство нулю геометрической суммы приложенных сил (см. § 3.4).

Пример. Рассмотрим однородную гладкую балку AB массой m, шарнирно закрепленную в точке A и опирающуюся на уступ D (рис. 4). Куда направлена реакция шарнира R?

На балку действуют три силы: неизвестная реакция шарнира R, сила тяжести m g, приложенная к ее середине и направленная вниз, и сила давления уступа N, направленная перпендикулярно балке*). Направления сил m g и N известны, следовательно, известна и точка их пересечения O. А так как балка находится в равновесии, то сила R тоже должна пройти через эту же точку, т.е. направлена вдоль линии AO.

Дата добавления: 2015-06-04