
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Эквивалентность пар сил
|
|
|
|
Векторный и алгебраический моменты пары сил.
Алгебраический момент M=±F•d (пара). M=±dF1=±dF2=±2SΔABC= ±S. Он не меняется при перемещении сил вдоль линии их действия (ни плечо, ни направление вращения не меняются).
Векторный момент – вектор M = M (F, F’), направлен перпендикулярно плоскости пары в ту сторону, откуда видно стремление пары повернуть тело против часовой хода стрелки, его модуль равен алгебраическому моменту пары.
M (F 1, F 2)= BA x F 1= AB x F 2.
7 вопрос
Рассмотрим две теоремы, характеризующие важные свойства пар сил.
Теорема 1. Пару сил в плоскости ее действия можно переносить в любое новое положение, действие пары на тело при этом не изменится.
Пусть дана пара  с плечом
с плечом 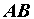 и требуется перенести ее так, чтобы плечо
и требуется перенести ее так, чтобы плечо 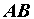 заняло произвольно выбранное положение
заняло произвольно выбранное положение  (рисунок а)
(рисунок а)

| 
| 
|
Через точки 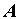 и
и  , а также
, а также 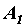 и
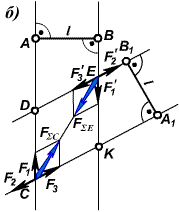
и 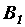 проведем прямые, перпендикулярные соответственно
проведем прямые, перпендикулярные соответственно 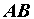 и
и  (рисунок б). Две первые параллельные линии пересекаются с двумя вторыми параллельными и образуют ромб
(рисунок б). Две первые параллельные линии пересекаются с двумя вторыми параллельными и образуют ромб 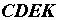 (так как дано
(так как дано 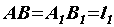 , а параллелограмм, у которого две высоты, проведенные из одной вершины, равны, - ромб). Силу
, а параллелограмм, у которого две высоты, проведенные из одной вершины, равны, - ромб). Силу 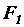 из точки
из точки 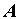 перенесем вдоль линии действия в точку
перенесем вдоль линии действия в точку 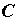 , а силу
, а силу  - из точки
- из точки  в точку
в точку  . В точке
. В точке 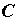 вдоль прямой
вдоль прямой  приложим уравновешенную систему сил
приложим уравновешенную систему сил  и
и  , равных по модулю
, равных по модулю  ; в точке
; в точке  вдоль прямой
вдоль прямой 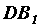 также приложим уравновешенную системы сил
также приложим уравновешенную системы сил 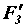 и
и 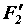 , равных по модулю
, равных по модулю  ; таким образом,
; таким образом, 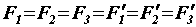 .
.
Определим равнодействующую  сил
сил 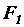 и
и  , приложенных к точке
, приложенных к точке 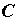 , и равнодействующую
, и равнодействующую 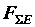 сил
сил 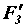 ,
,  приложенных к точке
приложенных к точке  . Легко видеть, что силы
. Легко видеть, что силы  и
и 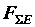 уравновешивают друг друга, так как они равны между собой по модулю и действуют по диагонали
уравновешивают друг друга, так как они равны между собой по модулю и действуют по диагонали 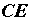 ромба
ромба 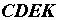 в противоположные стороны. Следовательно, силы
в противоположные стороны. Следовательно, силы 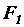 ,
,  ,
, 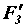 и
и  , образовавшие уравновешенную систему, можно исключить из рассмотрения. Остаются две силы - сила
, образовавшие уравновешенную систему, можно исключить из рассмотрения. Остаются две силы - сила  , которую из точки
, которую из точки 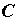 вдоль линии действия перенесем в точку
вдоль линии действия перенесем в точку 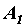 (рисунок в), и сила
(рисунок в), и сила 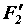 , которую из точки
, которую из точки  перенесем в точку
перенесем в точку 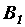 . Так как модули
. Так как модули 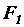 ,
,  ,
,  ,
, 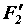 и плечи
и плечи 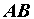 и
и  равны, то получаем пару
равны, то получаем пару  ,
, 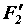 в положении
в положении  , эквивалентную паре
, эквивалентную паре 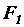 ,
,  в положении
в положении 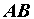 . Теорема доказана.
. Теорема доказана.
Перенося пару сил в любое положение в плоскости ее действия, мы тем самым переносим и точку приложения вектора момента пары, не меняя его ориентации в пространстве. Значит, вектор момента пары - свободный вектор.
Теорема 2. Две пары, расположенные в одной плоскости, производят на тело одинаковое вращательное действие в том случае, если их моменты равны.
 Предположим, что задана пара
Предположим, что задана пара  с плечом
с плечом 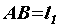 . Следовательно, момент пары
. Следовательно, момент пары  (рис. а). Присоединим к паре уравновешенную систему сил
(рис. а). Присоединим к паре уравновешенную систему сил 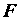 и
и  , действующих вдоль плеча
, действующих вдоль плеча 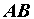 (рис. б), и сложим попарно силы
(рис. б), и сложим попарно силы 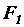 и
и 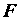 , а также
, а также  и
и  . Их равнодействующие
. Их равнодействующие  и
и 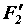 образуют новую пару сил с плечом
образуют новую пару сил с плечом 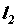 (рис. в). Все произведенные выше преобразования сделаны на основе аксиом статики и не нарушают состояния, в котором находилось тело, т. е. пара
(рис. в). Все произведенные выше преобразования сделаны на основе аксиом статики и не нарушают состояния, в котором находилось тело, т. е. пара 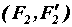 производит на тело такое же действие, как и пара
производит на тело такое же действие, как и пара  . Остается доказать равенство моментов этих пар сил:
. Остается доказать равенство моментов этих пар сил:
момент пары 
 ,
,
момент пары 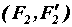
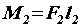 .
.
Из построений на рис. б видно, что  ,
, 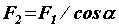 ; следовательно,
; следовательно, 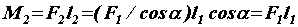 , т. е.
, т. е.  .
.
Теорема доказана.
Действующие в одной плоскости пары сил, моменты которых равны друг другу, называются статически эквивалентными.
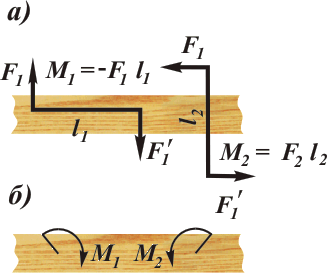 Из доказанных теорем следует, что вращательное действие расположенной в данной плоскости пары зависит только от ее момента, поэтому для задания пары сил достаточно указать числовое значение ее момента, а затем по данному или выбранному плечу можно определить силы пары или по силам подобрать необходимое плечо. Исходя из этого, на рисунках и схемах пары сил изображают иногда просто круговой стрелкой, характеризующей лишь направления вращающего действия. Например, пары
Из доказанных теорем следует, что вращательное действие расположенной в данной плоскости пары зависит только от ее момента, поэтому для задания пары сил достаточно указать числовое значение ее момента, а затем по данному или выбранному плечу можно определить силы пары или по силам подобрать необходимое плечо. Исходя из этого, на рисунках и схемах пары сил изображают иногда просто круговой стрелкой, характеризующей лишь направления вращающего действия. Например, пары  и
и 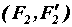 , приложенные к брусу (рис. а), можно условно изобразить круговыми стрелками, обозначив их
, приложенные к брусу (рис. а), можно условно изобразить круговыми стрелками, обозначив их 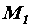 и
и  (рис. б).
(рис. б).
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 2161; Нарушение авторских прав?; Мы поможем в написании вашей работы!