Приведение пространственной произвольной системы сил к данному центру. Главный вектор и главный момент. Основная теорема статики

Пусть даны силы , приложенные к телу соответственно в точках (рис. 47, а). Осуществим преобразование данной пространственной произвольной системы сил, называемое приведением сил к данному центру. Выберем в теле произвольную точку О и в соответствии с леммой перенесем в эту точку все заданные силы. В результате получим новую систему сил, эквивалентную данной и состоящую из таких же сил, только приложенных в точке О, то есть сил 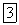, и присоединенных пар (рис. 47, б).

Силы 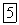являются сходящимися в точке О, и их можно заменить одной силой R (равнодействующей), приложенной в той же точке и равной геометрической сумме сил:

Рис. 47.

Совокупность всех присоединенных пар также можно заменить одной результирующей парой, момент которой равен геометрической сумме моментов всех присоединенных пар:

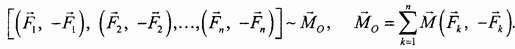
Выражая моменты присоединенных пар при помощи равенств , момент представим в виде

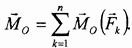
В результате проделанного преобразования вся совокупность заданных сил оказывается эквивалентной одной силе R и одной паре с моментом (рис. 47, в):

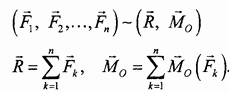
Введем два новых важных понятия.

Вектор R, равный геометрической сумме векторов всех заданных сил, называется главным вектором данной системы сил.

Вектор , равный геометрической сумме моментов всех заданных сил относительно центра О, называется главным моментом данной системы сил относительно центра О.

Теперь итоги выполненного преобразования можно сформулировать так. Всякую пространственную систему сил в общем случае можно заменить эквивалентной ей системой, состоящей из одной силы, равной главному вектору этой системы сил и приложенной в произвольно выбранной точке тела (центре приведения) и одной пары сил с моментом, равным главному моменту системы сил относительно выбранного центра приведения.

Это утверждение носит название основной теоремы статики.

Примечание. Не следует смешивать понятия главного вектора и равнодействующей системы сил. Равнодействующая, по определению, это сила, эквивалентная данной системе сил. Главный вектор представляет собой просто векторную сумму всех заданных сил. Как следует из основной теоремы статики, главный вектор эквивалентен данной системе сил только в совокупности с парой сил с моментом , и поэтому не может служить для нее равнодействующей. В дальнейшем будем пользоваться для равнодействующей обозначением .

11 вопрос

Дата добавления: 2015-06-04