Равновесие плоской системы сил. Случай параллельных сил

Необходимые и достаточные условия равновесия любой системы сил даются равенствами выражаемыми формулами (23). Найдем вытекающие отсюда аналитические условия равновесия плоской системы сил. Их можно получить в трех различных формах.

1. Основная форма условий равновесия. Так как вектор R равен нулю, когда равны нулю его проекции то для равновесия должны выполняться равенства где в данном случае — алгебраический момент, а любая точка в плоскости действия сил. Но из формул (27) следует, что предыдущие равенства будут выполнены, когда действующие силы удовлетворяют условиям:

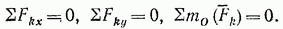
Формулы (29) выражают следующие аналитические условия равновесия: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю. Одновременно равенства (29) выражают условия равновесия твердого тела, находящегося под действием плоской системы сил.

2. Вторая форма условий равновесия: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительно каких-нибудь двух центров А и В и сумма их проекций на ось не перпендикулярную прямой АВ, были равны нулю:

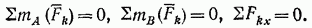(30)

Необходимость этих условий очевидна, так как если любое из них не выполняется, то или или и равновесия не будет. Докажем их достаточность. Если для данной системы сил выполняются только первые два из условий (30), то для нее Такая система сил, согласно результатам, полученным в § 15, может не находиться в равновесии, а иметь равнодействующую R, одновременно проходящую через точки А и В (рис. 52). Но по третьему условию должно быть Так как ось проведена не перпендикулярно к АВ, то последнее условие может быть выполнено, только когда т. е. когда имеет место равновесие.

3. Третья форма условий равновесия (уравнения трех моментов): для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительно любых трех центров А, В к С, не лежащих на одной прямой, были равны нулю:

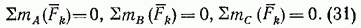
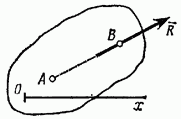
Рис. 52

Необходимость этих условий, как и в предыдущем случае, очевидна. Достаточность условий (31) следует из того, что если при одновременном выполнении этих условий данная система сил не находилась бы в равновесии, то она должна была бы приводиться к равнодействующей, одновременно проходящей через точки А, В и С, что невозможно, так как эти точки не лежат на одной прямой. Следовательно, при выполнении условий (31) имеет место равновесие.

Во всех рассмотренных случаях для плоской системы сил получаются три условия равновесия. Условия (29) считаются основными, так как при пользовании ими никаких ограничений на выбор координатных осей и центра моментов не налагается.

Если на тело наряду с плоской системой сил действует система лежащих в той же плоскости пар с моментами , то при составлении условий равновесия в уравнения проекций пары не войдут, так как сумма проекций сил пары на любую ось равна нулю. В уравнениях же моментов к моментам сил алгебраически прибавятся моменты пар, так как сумма моментов сил пары относительно любого центра равна моменту пары формула (15)]. Таким образом, например, условия равновесия (29) при действии на тело системы сил и пар примут вид:

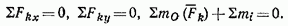
Аналогично преобразуются в этом случае условия (30) и (31),

Равновесие плоской системы параллельных сил. В случае, когда все действующие на тело силы параллельны друг другу, можно направить ось перпендикулярно силам, а ось параллельно им (рис. 53).

Тогда проекция каждой из сил на ось будет равна нулю и первое из равенств (29) обратится в тождество вида . В результате для параллельных сил останется два условия равновесия:

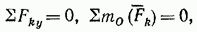
где ось параллельна силам.

Другая форма условий равновесия для параллельных сил, получающаяся из равенств (30), имеет вид:

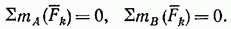
При этом точки А и В не должны лежать на прямой, параллельной силам.

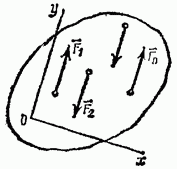
Рис. 53

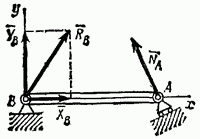
Рис. 54

13 вопрос

Дата добавления: 2015-06-04