
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Коэффициент трения скольжения
|
|
|
|
Коэффициент трения покоя
Определение коэффициента трения
Виды трения
Трение покоя проявляется в том случае, если тело находившееся в состоянии покоя, приводится в движение. Коэффициент трения покоя обозначается μ0.
Трение скольжения проявляется при наличии движения тела, и оно значительно меньше трения покоя.
| 1. | μск < μ 0 |
Трение качения проявляется в том случае, когда тело катится по опоре, и оно значительно меньше трения скольжения.
| 2. | μкач << μск |
Сила трения качения зависит от радиуса катящегося предмета. В типичных случаях (при расчетах трения качения колес поезда или автомобиля), когда радиус колеса известен и постоянен, его учитывают непосредственно в коэффициенте трения качения μкач.
 Коэффициент трения можно определить экспериментально. Для этого помещают тело на наклонную плоскость, и определяют угол наклона при котором:
Коэффициент трения можно определить экспериментально. Для этого помещают тело на наклонную плоскость, и определяют угол наклона при котором:
тело начинает двигаться
(коэффициент трения покоя μ0)
тело движется с постоянной скоростью
(коэффициент трения скольжения μ).
| 3. | μFн = Fс |
| 4. | μG cos (α) = G sin (α) |
| 5. | μ =tg (α) |
Здесь:
μ — искомый коэффициент трения,
α — угол наклона плоскости
14 вопрос
Пусть твердое тело под действием активных сил находится на шероховатой поверхности в предельном состоянии равновесия, когда сила трения достигает своего максимального значения 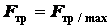 при данном значении реакции (рис. 1.28). В этом случае полная реакция шероховатой поверхности отклонена от нормали общей
при данном значении реакции (рис. 1.28). В этом случае полная реакция шероховатой поверхности отклонена от нормали общей  касательной плоскости трущихся поверхностей на наибольший угол
касательной плоскости трущихся поверхностей на наибольший угол  .
.
Угол между полной реакцией, построенной на наибольшей силе трения при данной нормальной реакции, и направлением нормальной реакции, называется углом трения
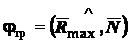 ;
; 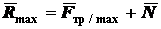 .
.
Из рис. 1.28 следует
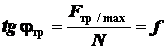 ;
; 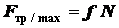 .
.
Тангенс угла трения равен коэффициенту трения
 .
.
Конус с вершиной в точке приложения нормальной реакции шероховатой поверхности, образующая которого составляет угол трения с этой нормальной реакцией, называется конусом трения (рис. 1.28).
Все максимальные реакции шероховатой поверхности направлены вдоль образующих конуса трения.
Если коэффициент трения во всех направлениях одинаков, то конус трения круговой.
Конус трения интересен тем, что ограниченная им область определяет область равновесия тела. Если линия действия равнодействующей активных сил проходит внутри конуса трения, то эта сила не сдвигает тело, как бы она не была велика. Если же линия действия равнодействующей активных сил расположена вне конуса трения, то эта сила сдвинет тело, как бы мала она не была.
15 вопрос
Если рассматриваемое тело имеет форму цилиндрического катка и под действием активных сил может катиться по поверхности другого тела, то из-за деформации поверхностей этих тел в месте их соприкосновения возникают силы реакции, препятствующие как скольжению, так и качению катка. Примерами таких катков являются различные колеса, например, колеса локомотивов, электровозов, вагонов, автомашин и т.д.
Пусть к оси катка весом 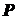 ,
,  находящегося на горизонтальной плоскости, приложена горизонтальная сила
находящегося на горизонтальной плоскости, приложена горизонтальная сила 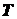 (рис. 1.29). Соприкосновение катка с плоскостью из-за их деформации происходит не вдоль одной образующей цилиндра, как в случае абсолютно твердых тел, а по некоторой площадке
(рис. 1.29). Соприкосновение катка с плоскостью из-за их деформации происходит не вдоль одной образующей цилиндра, как в случае абсолютно твердых тел, а по некоторой площадке 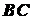 . Точка приложения реакций
. Точка приложения реакций 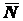 и
и 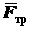 будет находиться в некоторой точке
будет находиться в некоторой точке 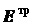 этой площадки.
этой площадки.
Из условий равновесия катка имеем
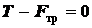 ;
; 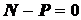 ;
; 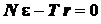 .
.
На каток действуют две уравновешенные пары сил
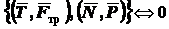 .
.
Пара 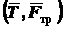 стремится привести каток в движение; пара
стремится привести каток в движение; пара 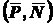 препятствует движению.
препятствует движению.
Момент пары 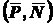 называется моментом сопротивления качению.
называется моментом сопротивления качению.
Итак, реакция плоскости на каток состоит из нормальной реакции 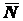 , касательной реакции
, касательной реакции 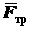 (силы трения качения), из пары трения качения
(силы трения качения), из пары трения качения 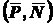 с моментом сопротивления качению.
с моментом сопротивления качению.
Установлены следующие приближенные законы трения качения.
Первый закон. Максимальный момент пары сил, препятствующий качению, в широких пределах не зависит от радиуса катка.
Второй закон. Максимальный момент сопротивления качению пропорционален силе нормального давления катка на опорную плоскость и достигается в момент выхода катка из положения равновесия
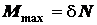 ;
; 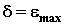
(условие начала качения катка).
Коэффициент 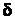 называют коэффициентом трения качения или коэффициентом трения 2-го рода. Он имеет размерность длины.
называют коэффициентом трения качения или коэффициентом трения 2-го рода. Он имеет размерность длины.
Коэффициент трения качения равен плечу пары сопротивления качения при предельном равновесии катка (рис. 1.29).
Третий закон. Коэффициент трения качения зависит от материала катка, опорной плоскости, а также от физического состояния их поверхностей.
В момент начала качения катка (выхода катка из положения равновесия) имеем (рис. 1.29)
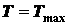 ;
; 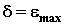 ;
; 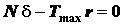 .
.
Коэффициенты трения качения устанавливаются экспериментально.
Приведем значения коэффициентов трения качения для некоторых материалов (в см):
Стальной каток по стали............... 0,005
Деревянный каток по стали............. 0,03 – 0,04
Деревянный каток по дереву............. 0,05 – 0,08
Колесо вагона по рельсу..............» 0,05
Резиновая шина по шоссе..............» 0,024
Коэффициент трения качения при качении можно считать не зависящим от угловой скорости качения катка и его скорости скольжения по плоскости.
Законы трения качения, как и законы трения скольжения, справедливы для не очень больших давлений и не слишком легко деформируемых материалов катка и плоскости.
Вычислим тяговую силу, необходимую для начала скольжения тела и для начала качения катка радиуса  одинакового веса по горизонтальной плоскости
одинакового веса по горизонтальной плоскости
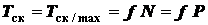 ;
;
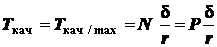 .
.
Обычно 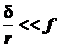 . Следовательно, для начала качения требуется значительно меньшая сила, чем для начала скольжения тела одинакового веса по горизонтальной плоскости. С точки зрения затрат энергии выгодно заменять скольжение качением. Изобретение колеса примерно 5000 лет назад явилось огромным достижением человечества по пути борьбы с трением.
. Следовательно, для начала качения требуется значительно меньшая сила, чем для начала скольжения тела одинакового веса по горизонтальной плоскости. С точки зрения затрат энергии выгодно заменять скольжение качением. Изобретение колеса примерно 5000 лет назад явилось огромным достижением человечества по пути борьбы с трением.
Задача 1.7. Однородный брус опирается  в точке
в точке 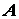 на негладкий горизонтальный пол и удерживается в точке
на негладкий горизонтальный пол и удерживается в точке 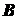 веревкой (рис. 1.30). Коэффициент трения бруса о пол равен
веревкой (рис. 1.30). Коэффициент трения бруса о пол равен 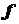 . При каком угле
. При каком угле 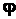 наклона веревки к горизонту брус начнет скользить по полу? Угол
наклона веревки к горизонту брус начнет скользить по полу? Угол 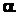 образуемый брусом с полом, равен
образуемый брусом с полом, равен 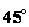 .
.
Решение. Рассмотрим равновесие бруса. Освободим брус от связей, приложим к нему реакции связей. На брус действуют силы 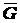 ,
, 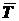 (натяжение веревки),
(натяжение веревки), 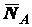 ,
, 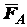 (нормальная и касательная составляющие реакции горизонтальной плоскости).
(нормальная и касательная составляющие реакции горизонтальной плоскости).
Составим условия равновесия
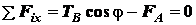 ;
;
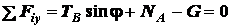 ;
;
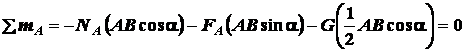 .
.
На основании закона Кулона имеем
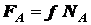 .
.
Последовательно получаем зависимости
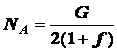 ; (
; ( 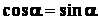 ;
; 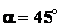 );
);
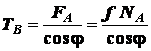 ;
;
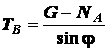 .
.
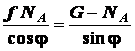 ;
;
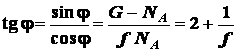 .
.
Итак,
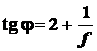 .
.
Задача 1.8. Цилиндрический каток радиуса 
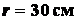 и весом
и весом 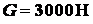 приводится в равномерное движение человеком, который давит на рукоятку
приводится в равномерное движение человеком, который давит на рукоятку 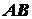 с постоянной силой
с постоянной силой 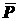 в направлении
в направлении 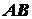 (рис. 1.31, а). Коэффициент трения качения катка
(рис. 1.31, а). Коэффициент трения качения катка 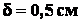 , коэффициент трения скольжения между катком и дорогой
, коэффициент трения скольжения между катком и дорогой 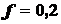 . Определить величину силы
. Определить величину силы 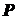 и нормальную реакцию горизонтальной плоскости. Рукоятка
и нормальную реакцию горизонтальной плоскости. Рукоятка 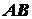 составляет с горизонталью угол
составляет с горизонталью угол 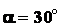 .
.
Решение. Рассмотрим равновесие катка. Освободим каток от связей, приложим к нему реакции связей (рис. 1.31, б). На каток действуют силы 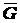 и
и 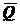 (давление рукоятки на шарнир
(давление рукоятки на шарнир 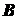 ),
), 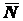 ,
, 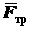 (нормальная и касательная составляющие реакции горизонтальной плоскости), причем
(нормальная и касательная составляющие реакции горизонтальной плоскости), причем 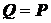 .
.
Уравнения равновесия имеют вид
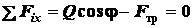 ; (а)
; (а)
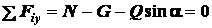 ; (б)
; (б)
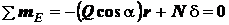 . (в)
. (в)
Из (а), (б), (в) находим
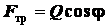 ;
;
 ;
;
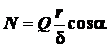 .
.
Далее получаем
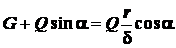 ;
;
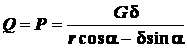 .
.
Выполним вычисления:
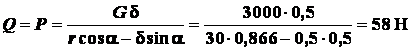 ;
;
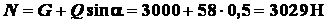 .
.
Проверим выполнение условия качения катка без скольжения
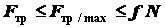 .
.
Вычислим силу трения качения и силу трения скольжения
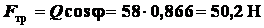 ;
;
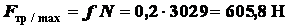 .
.
Таким образом, сила трения качения меньше силы трения скольжения. Каток будет катиться бег скольжения.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 1563; Нарушение авторских прав?; Мы поможем в написании вашей работы!