
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема Вариньона
|
|
|
|
В некоторых случаях при определении момента силы возникают трудности в расчете плеча силы.
Решение вопроса упрощает теорема Вариньона, согласно которой момент равнодействующей системы сил относительно какого-либо центра равен геометрической сумме моментов составляющих систему сил относительно того же центра.

Рисунок 1.17
Например, момент силы F относительно точки O можно определить как алгебраическую сумму моментов сил Fx и Fy (на которые можно разложить силу F) относительно той же точки O (рисунок 1.17). То есть
Mo(F)= -Fh = -Fx y+ Fy x, (1.8)
где Fx, Fy, x и y – проекции на оси координат силы F и радиуса-вектора r.
12 вопрос
Из основных аксиом статики следуют элементарные операции над силами:
1) силу можно переносить вдоль линии действия;
2) силы, линии действия которых пересекаются, можно складывать по правилу параллелограмма (по правилу сложения векторов);
3) к системе сил, действующих на твёрдое тело, можно всегда добавить две силы, равные по величине, лежащие на одной прямой и направленные в противоположные стороны.
Элементарные операции не изменяют механического состояния системы.
Назовём две системы сил эквивалентными, если одна из другой может быть получена с помощью элементарных операций (как в теории скользящих векторов).
Система двух параллельных сил, равных по величине и направленных в противоположные стороны, называется парой сил (рис.12).
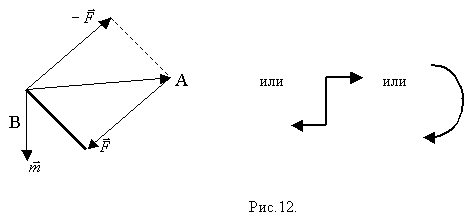
Момент пары сил  - вектор, по величине равный площади параллелограмма, построенного на векторах пары, и направленный ортогонально к плоскости пары в ту сторону, откуда вращение, сообщаемое векторами пары, видно происходящим против хода часовой стрелки.
- вектор, по величине равный площади параллелограмма, построенного на векторах пары, и направленный ортогонально к плоскости пары в ту сторону, откуда вращение, сообщаемое векторами пары, видно происходящим против хода часовой стрелки.
 , то есть момент силы
, то есть момент силы  относительно точки В.
относительно точки В.
Пара сил полностью характеризуется своим моментом.
Пару сил можно переносить элементарными операциями в любую плоскость, параллельную плоскости пары; изменять величины сил пары обратно пропорционально плечам пары.
Пары сил можно складывать, при этом моменты пар сил складываются по правилу сложения (свободных) векторов.
Приведение системы сил, действующих на твёрдое тело, к произвольной точке (центру приведения) - означает замену действующей системы более простой: системой трёх сил, одна из которых проходит через наперёд заданную точку, а две другие представляют пару.
Доказывается с помощью элементарных операций (рис.13).
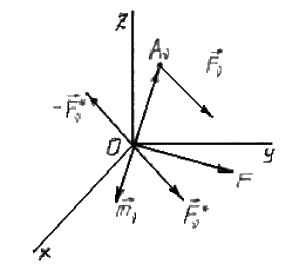
Рис.13.
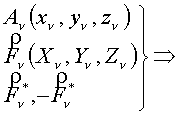 Система сходящихся сил
Система сходящихся сил 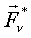 и система пар сил
и система пар сил 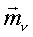 .
.
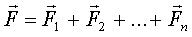 - результирующая сила
- результирующая сила 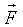 .
.
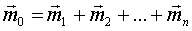 - результирующая пара
- результирующая пара 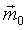 .
.
Что и требовалось показать.
Две системы сил будут эквивалентны тогда и только тогда, когда обе системы приводятся к одной результирующей силе и одной результирующей паре, то есть при выполнении условий:
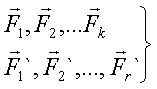
| 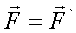 , , 
|
Общий случай равновесия системы сил, действующих на твёрдое тело
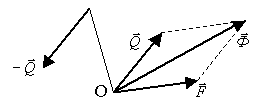
Рис.14.
Приведём систему сил к (рис.14):
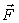 - результирующая сила через начало координат;
- результирующая сила через начало координат;
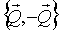 - результирующая пара, причём,
- результирующая пара, причём, 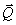 через точку О.
через точку О.

То есть привели к 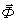 и
и 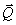 - две силы, одна из которых
- две силы, одна из которых 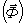 проходит через заданную точку О.
проходит через заданную точку О.
Равновесие, если 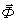 и
и 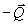 на одной прямой, равны, направлены противоположно (аксиома 2).
на одной прямой, равны, направлены противоположно (аксиома 2).
Тогда 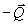 проходит через точку О, то есть
проходит через точку О, то есть 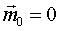 .
.
Далее: 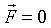 , так как остаётся только эта сила.
, так как остаётся только эта сила.
Итак, общие условия равновесия твёрдого тела:
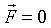 ,
, 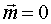 .
.
Эти условия справедливы для произвольной точки пространства.
Контрольные вопросы:
1. Перечислите элементарные операции над силами.
2. Какие системы сил называются эквивалентными?
3. Напишите общие условия равновесия твёрдого тела.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 605; Нарушение авторских прав?; Мы поможем в написании вашей работы!