Трение. Трение покоя и трение скольжения

Силы “сухого” трения возникают при соприкосновении поверхностей твердых тел. Если эти тела неподвижны друг относительности друга – может возникнуть сила трения покоя, если есть относительное движение – сила трения скольжения.

Сила трения покоя. Рассмотрим брусок, лежащий на горизонтальной поверхности (рис. 1а). На него действуют сила тяжести m g и сила реакции опоры N. Брусок покоится, потому что эти две силы компенсируют друг друга; силы, пытающейся сдвинуть брусок вдоль поверхности нет, поэтому и нет никакой силы трения.

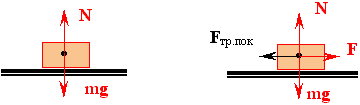
Рис. 1а. Рис. 1б.

Подействуем на брусок с небольшой силой F, направленной вдоль поверхности (рис. 1б). Если брусок по-прежнему не сдвигается с места, то, значит, возникает сила трения покоя F _тр.пок., равная по величине и направленная против пытающейся сдвинуть брусок силы F:

F _тр.пок. = - F

Будем увеличивать “сдвигающую” силу F. Пока брусок остается в покое, сила трения покоя так же увеличивается. При некоторой, достаточно большой, сдвигающей силе F брусок придет в движение, и сила трения покоя превращается в силу трения скольжения. Это означает, что сила трения покоя не может увеличиваться до бесконечности – существует верхний предел, больше которого она быть не может. Величина этого предела – значение силы трения скольжения:

F _{тр.пок.предел} = F _{тр.скольж}

А от чего зависит сила трения скольжения? Она, напротив, не зависит от величины сдвигающей силы, а определяется только двумя факторами: природой и качеством соприкасающихся поверхностей (коэффициентом трения скольжения μ) и силой, прижимающей одно тело к другому (а, значит,и силой реакции опоры N):

F_{тр.скольж} = μ N

Сила трения скольжения всегда направлена против относительной скорости скольжения соприкасающихся тел. Величина этой силы слабо зависит от величины скорости, поэтому при решении задач ее считают постоянной по величине.

Пример 1. Плоскость наклонена под углом α к горизонту. С каким ускорением будет двигаться по ней брусок, если коэффициент трения между бруском и плоскостью равен μ?

Решение. На брусок действуют три силы: тяжести m g, реакции опоры N и сила трения F _тр(рис. 2). По второму закону Ньютона:

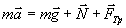
(6)

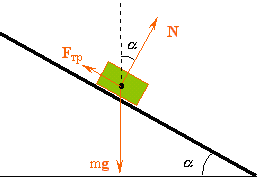
Рис. 2.

Относительно силы трения заранее известно только то, что она направлена вдоль наклонной плоскости. То же можно сказать о направлении ускорения. Характер движения бруска зависит от начальных условий: мы могли в начальный момент времени сообщить бруску некоторую скорость, направленную а) вниз по наклонной плоскости, б) вверх по наклонной плоскости, в) куда-нибудь вбок, г) не сообщать никакой начальной скорости (осторожно положить брусок на наклонную плоскость) – ведь от этого зависит направление силы трения, а также то, будет она силой трения скольжения или силой трения покоя.

Запишем уравнение (6) в проекции на направление поперек наклонной плоскости:

0 = - mgCosα + N (7)

Видно, что сила реакции опоры в данном примере не зависит характера движения бруска и равна mgCosα.

Рассмотрим сначала наиболее простой случай г) – состояние покоя бруска (а = 0). В проекции на ось вдоль наклонной плоскости уравнение (6) запишется:

0 = mgSinα - F_тр.пок.

Откуда: F_тр.пок. = mgSinα

Видно, что для обеспечения покоя бруска сила трения покоя должна возрастать с увеличением угла α. Но мы знаем, что она не может быть больше максимального значения – силы трения скольжения:

F_тр.пок. ≤ F_{тр.пок.предел} = F_{тр.скольж} = μ N = μ mgCosα.

Поэтому ясно, что существует предельный угол α _пр наклона плоскости, при котором покой бруска станет невозможным, начнется соскальзывание. Значение этого угла найдем из условия, что сила трения покоя становится максимальной:

F_тр.пок. = F_{тр.пок.предел}

mgSinα _пр = μ mgCosα _пр

Откуда: tg α _пр = μ

Видно, что предельный угол не зависит от массы бруска. Последнее соотношение позволяет на практике определить значение коэффициента трения.

При α > α _пр брусок будет соскальзывать вниз по наклоной плоскости. Сила трения скольжения, как всегда, направлена против движения (рис. 2). Проекция уравнения (6) на направление вдоль плоскости будет:

ma = mgSinα - F_{тр.скольж}

Подставляя в это равенство значение силы трения скольжения

F_{тр.скольж} = μ mgCosα, получим значение ускорения бруска

a = g(Sinα - μ Cosα) (8)

Ускорение бруска не зависит от его массы. При α > α _пр (8) дает положительное значение ускорения, при α < α _пр значение ускорения формально отрицательно, что не имеет физического смысла в случае г), когда брусок вначале был неподвижен, но имеет смысл в случае а), когда бусок движется вниз по плоскости благодаря скорости, которую он уже имел в начальный момент времени – в этом случае он будет двигаться замедленно и в конце концов остановится. Это следует из того, что для получения (8) мы использовали только тот факт, что сила трения направлена вверх по наклонной плоскости.

В случае б) сила трения будет сначала направлена вниз по наклонной плоскости и, легко убедиться, что ускорение бруска будет направлено вниз вдоль наклоной плоскости и равно:

a = g(Sinα + μ Cosα) (9)

Это ускорение равнозамедленого движения бруска вверх, пока он не остановится в верхней точке. Дальше брусок либо останется в покое в этой точке, если α < α _пр, либо начнет соскальзывать вниз с ускорением (8), если α > α _пр .

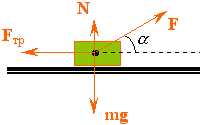
Рис. 3.

Пример 2. Необходимо тянуть брусок массой m при помощи нити по горизонтальной поверхности. Под каким углом α к горизонту надо приложить силу тяги F, чтобы она была минимальной (рис. 3)?

Коэффициент трения между бруском и поверхностью равен μ.

Решение. На брусок действуют силы: тяжести m g, трения скольжения F_тр, реакции опоры N и тяги F. По второму закону Ньютона:

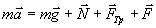
Ясно, что сила тяги будет минимальной, когда ускорение бруска будет равно нулю, т.е. если тянуть его равномерно:

(*)

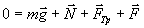
В проекциях на горизонтальное и вертикальное направления получим:

0 = - F_тр + FCosα (10)

0 = - mg + N + FSinα (11)

Сила трения скольжения F_тр = μ N, а из (11): N = mg - FSinα. Тогда из (10)

μ (mg - FSinα) = FCosα

Откуда

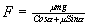
(12)

Мы нашли функциональную зависимость величины силы тяги от угла α. Очевидно, F будет наименьшей при наибольшем значении знаменателя. Таким образом, надо найти такой угол α, при котором функция

f(α) = Cosα + μ Sinα

принимает наибольшее значение. Известно, что для этого необходимо приравнять к нулю производную функции:

f `(α) = - Sinα + μ Cosα = 0

Sinα = μ Cosα (13)

Находим, что значение функции f(α) максимально при tgα = μ. (Под таким углом надо направлять силу тяги). При этом f(α) = 1/Cosα. Подставляя в (12), получим минимальное значение силы тяги

F_min = μ mg Cosα

или с учетом (13)

F_min = mgSinα (14)

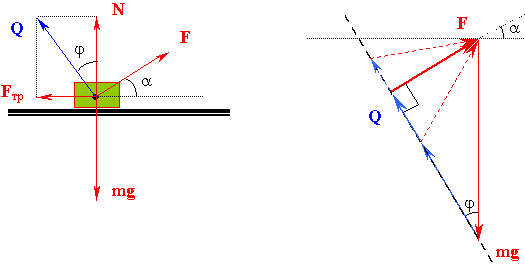
Рис. 4а. Рис. 4б

Можно обойтись и без помощи понятия производной функции. Рассмотрим вместо сил N и F_тр их сумму Q (рис. 4а). Эта сумма направлена под углом φ к вертикали, причем tgφ = F_тр/N = μ N/N = μ. Важно отметить, что при изменении силы реакции опоры N (а, значит, и силы трения скольжения F_тр = μ N) значение этого угла φ остается всегда одним и тем же. Тогда вместо (*) запишем условие равномерного движения бруска:

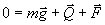
(14)

и найдем минимальное значение силы тяги F графически. Для этого из некоторой точки отложим сначала вертикально вниз вектор силы тяжести m g (рис. 4,б). Из конца вектора m g под известным углом φ = arctgμ мы должны отложить следующий вектор суммы Q. Величина его нам пока неизвестна, но его конец должен лежать на пунктирной прямой, проведенной под углом φ к вертикали. Наконец, в соответствии с (14), вектор силы F должен замыкать треугольник сил – соединять конец вектора Q с началом вектора m g. Как видно из рис. 6,б, величина силы F будет минимальна тогда, когда она будет перпендикулярна силе Q (в этом случае α = φ и tgα = tgφ = μ). Тогда:

F_min = mgSinφ = mgSinα

получили те же результаты, что и выше.

Коэффициент трения устанавливает пропорциональность между силой трения и силой нормального давления, прижимающей тело к опоре. Коэффициент трения является совокупной характеристикой пары материалов которые соприкасаются и не зависит от площади соприкосновения тел.

Дата добавления: 2015-06-04