
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
По горизонталям и уклонов линий
|
|
|
|
Определение отметок точек. Если точки располагаются на горизонталях, то их отметки будут равны высотам этих горизонталей. Отметки самих горизонталей определяются по высоте сечения рельефа, указанной на карте, и отметкам точек Земли, отмеченных непосредственно на карте (рис.24). Например, на рис.22,а отметка вершины т.А равна 121,3 м, а т.В расположена по спуску на второй горизонтали от точки А. Если отметка первой горизонтали равна 120 м (при hс = 2 м), то отметка второй горизонтали и, следовательно, точки В будет равна 118 м. Или на рис.24,б отметка дна впадины т.А равна 170,6 м, а точка В расположена с повышением на второй горизонтали от точки А. Если отметка первой горизонтали равна 171 м (при hc = 1 м), то отметка второй горизонтали и, следовательно, точки В будет равна 172 м. Аналогичные примеры приведены на рис.24,в,г,д. На рис.24,е дана отметка одной из горизонталей (110 м) и здесь отметка следующей горизонтали определяется путём последовательного прибавления (вычитания) величины сечения рельефа (hс) – отметка точки В будет равна 110 м + 0,5 м + 0,5 м = 111 м (при hс = 0,5 м).
Если точки располагаются между горизонталями, то их отметки определяются путём интерполирования их отметок. Например, точка с расположена между горизонталями с отметками 123 и 124 м (при hс = 1 м) (рис.25,а). Отсюда можно представить разрез местности по направлению линии ав (см. рис.25,б).
|
 В С
В С










 h х +
h х + 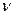 А
А



|
 в в с а
в в с а
 с
с
а НВ = 124 м НС На = 123 м
124 123

Уровень моря
Рис.25. Схема интерполирования при определении отметки точки С:
а – схема расположения точки С б – схема расположения точки С
на плане; на местности
Из анализа рис. 25,б следует, что отметка искомой точки С будет равна отметки точки (горизонтали) А плюс отрезок х. Величина х может быть получена из решения пропорции для двух подобных треугольников:  Вва и
Вва и  Сса
Сса 
 или х =
или х = 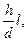 (20)
(20)
где h – превышение между двумя горизонталями, hc; d - расстояние между точками А и В на плане ав; l – расстояние между точками А и С на плане ас.
Например, на плане расстояния d и l между точками ав и ас равны соответственно: d = 30 мм и l = 20 мм.
Тогда, используя формулу (20), получим х =  .
.
Отсюда отметка искомой точки равна
Нс = На + х = 123 м + 0,7 м = 123,7 м.
Определение уклонов. Характер местности на картах и планах определяется не только наличием тех или иных форм рельефа (см. табл.5), но и величинами наклона её поверхности к горизонту. Величину наклона можно определить по тем же горизонталям (рис.25), откуда видно, что линия АВ местности наклонена к горизонту (к линии ав) под углом 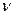 . Тангенс этого угла называется уклоном линии и обозначается латинской буквой i
. Тангенс этого угла называется уклоном линии и обозначается латинской буквой i
i = tg 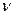 =
= 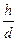 , (21)
, (21)
уклон линии равен отношению превышения между концами данной линии к горизонтальному проложению этой линии.
В примере на рис. 25,б превышение между точками А и В равно 1 м, горизонтальное расстояние между ними на плане (см. рис.23,а) в масштабе 1:2000 равно d = 30 мм х 2000 = 60 м и уклон линии АВ будет равен
i = 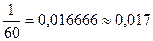 .
.
В инженерной практике уклоны рассчитываются до 0,001, вычисление уклона с большей точностью не имеет практического смысла. Записывают уклоны или в уклонах i, или в процентах %, или в промилях 0/00. В данном примере i = 0,017 = 1,7% = 170/00.
Наличие такого уклона означает, что по данному направлению линия повышается или понижается через каждые 100 м горизонтального расстояния на 1, 7 м, а через 1 км – на 17 м.
Полученная величина уклона ещё не до конца характеризует участок местности – нет информации о направлении повышения или понижения линии, то есть перед значением уклона следует проставлять знак + или -. Знак уклона зависит от положительного или отрицательного значения превышения. Знак превышения определяется в процессе нахождения разности отметок концов данной линии: h = НВ – НА, при определении превышения следует из отметки конечной точки НВ вычитать отметку начальной точки НА.
Здесь следует отметить, что полученный уклон характеризует местность только в том случае, если линия совпадает с её поверхностью. В противном случае это только наклон линии. Характер же местности определяется крутизной её скатов.
3.4.2.3. Определение крутизны ската.
Масштабы (графики) заложений
Мерой крутизны ската служит его уклон, определяемый тангенсом угла наклона линии ската к горизонту (см. формулу 21). Для определения крутизны следует в указанной формуле использовать превышение между соседними горизонталями, hс
i = tg  , (22)
, (22)
где hс – сечение рельефа, м; d – заложение, м.
Только в этом случае будет найден уклон местности на этом участке (рис.26).
 В
В


 Плоскости сечения d Местность
Плоскости сечения d Местность
рельефа

Р
А В

 d
d
Заложение
 |  |

Соседние на плане горизонтали
Рис.26. Схема определения по плану крутизны ската
Таким образом, для определения крутизны ската по тому или иному направлению необходимо измерить расстояние между соседними горизонталями в масштабе данной карты или плана и по формуле (22) найти уклон, величина превышения берётся по указанному на карте или плане высоте сечения рельефа (рис.27)



 n k l 125125
n k l 125125
|

Рис. 27. Схема различной крутизны ската по разным направлениям
Отсюда следует, при определении крутизны ската по разным направлениям величина превышения не меняется и равна высоте сечения рельефа. Следовательно, чем меньше расстояние между соседними горизонталями, тем круче скат.
Из анализа вышесказанного следует, что при определении крутизны ската можно пользоваться специальным графиком, который называется масштабом (графиком) заложений. Как правило, графики строятся на каждой карте или плане в их масштабе с учётом принятой для них высоты сечения рельефа, записав формулу (22) в следующем виде:
для уклонов – d =hc/i и для углов наклона - d = hc ctg 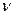 (23)
(23)
Построение графиков сводится к следующему. На вертикальных линиях (для уклонов и для углов наклона) откладываются произвольные отрезки, подписывая их в порядке возрастания уклонов или углов наклона (рис.28)
Через точки деления проводятся горизонтальные линии, на которых откладываются в масштабе данной карты или плана вычисленные по формулам (23) величины заложений d. Концы этих заложений соединяются плавной кривой.
Масштабы заложений
i 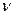

 в уклонах в углах наклона
в уклонах в углах наклона




 1,00 450
1,00 450

 0,90 М 1:2000 40
0,90 М 1:2000 40


 0,80 Высота сечения рельефа 1 м 30
0,80 Высота сечения рельефа 1 м 30


 0,70 20
0,70 20

 0,60 15
0,60 15

 0,50 10
0,50 10

 0,40 9
0,40 9

 0,30 8
0,30 8

 0,20 7
0,20 7

 0,10 6
0,10 6

 0,08 5
0,08 5

 0,06 4
0,06 4

 0,04 M-N M-N 3
0,04 M-N M-N 3

 0,03 2
0,03 2

 0,02 1
0,02 1

 0,01 0000/
0,01 0000/
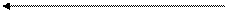
 d
d
Рис. 28 Схема построения графиков заложений
Пользуются полученными графиками следующим образом: раствором циркуля-измерителя на карте берётся отрезок (заложение) между соседними горизонталями по заданному направлению ската, этот размер переносится на тот или иной график, совмещая одну ножку циркуля с вертикальной линией графика, а другую – с кривой по горизонтальному направлению. По ножке циркуля на вертикальной линии берётся величина уклона или угла наклона. На рис. 28 уклон линии M-N ската равен i = 0,03, а угол наклона - 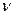 = 20.
= 20.
3.4.2.4. Проведение на картах и планах
линий заданного уклона
Пользуясь графиками заложений, можно решать обратные задачи, например, находить на картах и планах положение линий с заданным уклоном. Такая задача часто встречается в инженерной практике при трассировании линейных сооружений. Для этого размером циркуля берется с графика отрезок, соответствующий заданному уклону или углу наклона, и переносится на карту или план, совмещая концы циркуля с соседними горизонталям. Концы циркуля и будут показывать направление линии заданного уклона. Здесь следует ещё раз подчеркнуть, что пользоваться графиками можно лишь на картах и планах, для которых они построены, то есть имеется полное соответствие масштаба и высоты сечения рельефа карты и графика.
Например, на плане масштаба 1:2000 с сечением рельефа 1 м необходимо найти между точками А и В линию с уклоном i = 0,050 (рис.29).

 d А
d А

|



 152
152
заложение,
 равное уклону
равное уклону

 1 n
1 n
0,050 или 5% k
 151
151
 l
l
|


 11
11
 f 149
f 149
В 148
М 1:2000
Высота сечения рельефа 1 м
Рис.29. Схема проведения на плане линии заданного уклона
В этом случае поступают следующим образом. Точки А и В соединяют прямой и с графика заложений берут отрезок d, равный заданному уклону I = 0,05 (см. рис.29, отрезок d). При этом следует вспомнить то, о чём шла речь в предыдущем параграфе: если отрезок заданного размера (уклона) своими концами касается по кратчайшему направлению двух соседних горизонталей, то в этом направлении уклон местности соответствует заданному уклону; если отрезок больше, чем кратчайшее расстояние между смежными горизонталями, то его следует повернуть до совпадения концов со смежными горизонталями, и в этом направлении местность будет иметь заданный уклон; если же отрезок своими концами не достаёт до смежных горизонталей, то здесь местность во всех направлениях имеет уклон меньше, чем заданный, и следует остановиться на кратчайшем направлении. Необходимо также отметить, что искать направления линии заданного уклона следует вблизи прямой АВ или совпадающие с ней, укладка каждого последующего отрезка нужно начинать от конца предыдущего.
На рис.29 отрезок d не поместился между горизонталями 152 и 151 по кратчайшему направлению и пришлось наметить два варианта – Аm и Аn.
Видно, что второй вариант лучше, так как расположение отрезка оказалось ближе к прямой АВ. Однако это не значит, что первый вариант следует сразу отбрасывать, так как ещё неизвестно результаты дальнейшего трассирования. Поэтому нужно продолжать поиски положения линии заданного уклона по этим вариантам до конца и только потом оценивать эти варианты, например, с позиции коэффициента развития этой линии (трассы).
Коэффициент развития К – это соотношение длины найденной ломаной линии по отношению к исходной длине прямой, соединяющей заданные точки АВ
К1 =  и К2 =
и К2 =  . (24)
. (24)
В данном примере без каких-либо расчётов видно, что второй вариант действительно оказался предпочтительней, так как линия получилась ближе к прямой АВ (коэффициент развития меньше).
3.4.2.5. Построение профилей местности
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 4975; Нарушение авторских прав?; Мы поможем в написании вашей работы!