
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Випадки приведення просторової системи сил до найпростішого виду
|
|
|
|
Будь-яка просторова система сил приводиться до однієї сили - головного вектора  - та однієї пари сил, момент якої дорівнює головному моменту
- та однієї пари сил, момент якої дорівнює головному моменту  . Можливі такі випадки:
. Можливі такі випадки:
а) для даної системи сил головний вектор  і головний момент
і головний момент  дорівнюють нулю (
дорівнюють нулю ( ) - система знаходиться в рівновазі. При цьому діючі сили задовольняють умовам рівнянь (8.14) і (8.15);
) - система знаходиться в рівновазі. При цьому діючі сили задовольняють умовам рівнянь (8.14) і (8.15);
б) якщо для даної системи сил  , а
, а 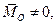 то система приводиться до пари сил, момент якої обчислюється за допомогою формул (8.7) і (8.8). Напрямні косинуси вектора
то система приводиться до пари сил, момент якої обчислюється за допомогою формул (8.7) і (8.8). Напрямні косинуси вектора  визначаються за формулами (8.9);
визначаються за формулами (8.9);
в) якщо для даної системи сил 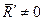 , а
, а  то система приводиться до рівнодіючої
то система приводиться до рівнодіючої  , яка проходить через центр приведення О та обчислюється за допомогою формул (8.4), (8.5), (8.6);
, яка проходить через центр приведення О та обчислюється за допомогою формул (8.4), (8.5), (8.6);
 г) якщо для даної системи сил
г) якщо для даної системи сил 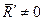 і
і 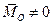 , але
, але  (рис. 8.4), то ця система сил також приводиться до однієї рівнодіючої, яка дорівнює
(рис. 8.4), то ця система сил також приводиться до однієї рівнодіючої, яка дорівнює  і прикладена в точці А.
і прикладена в точці А.
Відстань ОА обчислюється за формулою:

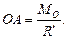 (8.16)
(8.16)
Вектор 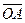 направлений так, щоб обертання навколо точки О силою
направлений так, щоб обертання навколо точки О силою  відбувалось проти ходу годинникової стрілки;
відбувалось проти ходу годинникової стрілки;
д) якщо для даної системи сил 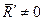 і
і 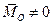 , а
, а 
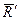 II
II 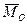 (рис. 8.5 а), то система сил приводиться до однієї сили
(рис. 8.5 а), то система сил приводиться до однієї сили 
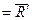 і пари сил
і пари сил 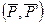 , яка лежить у площині, перпендикулярній до сили
, яка лежить у площині, перпендикулярній до сили  . Така сукупність сили та пари сил називається динамічним гвинтом або динамою. Пряма, уздовж якої направлений вектор
. Така сукупність сили та пари сил називається динамічним гвинтом або динамою. Пряма, уздовж якої направлений вектор  , називається віссю динами (рис. 8.5 б);
, називається віссю динами (рис. 8.5 б);
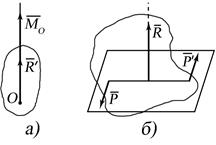
 е) якщо для даної системи сил
е) якщо для даної системи сил 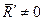 ,
, 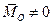 і
і 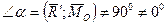 , то така система сил також приводиться до динами, але вісь динами не проходить через точку О, а проходить через точку А (рис. 8.6 а, б). При цьому:
, то така система сил також приводиться до динами, але вісь динами не проходить через точку О, а проходить через точку А (рис. 8.6 а, б). При цьому:


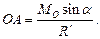 (8.17)
(8.17)
Рівняння центральної гвинтової осі мають вигляд:
 (8.18)
(8.18)
Вказівка. Для закріплення теоретичного матеріалу § 8 необхідно розв’язати наступні задачі із збірника: Мещерский И.В. Сборник задач по теоретической механике. - М.: Наука, 1981 (або 1986):
1) №№ 8.12 - 8.16;
2) №№ 8.17; 8.19; 8.21; 8.24; 8.28; 8.36;
3) №№ 8.31; 8.33; 8.37 - 8.39.
Питання для самоконтролю
1. Сформулюйте теорему про паралельний перенос сили.
2. Яка система сил називається довільною просторовою системою сил?
3. Опишіть зведення довільної просторової системи сил до однієї сили та пари сил.
4. Що називається головним вектором системи сил?
5. Чи є головний вектор еквівалентним до системи сил?
6. Що називається головним моментом системи сил відносно центра зведення?
7. Чим у загальному випадку можна замінити довільну просторову систему сил?
8. Як визначаються величина та напрямок головного вектора довільної просторової системи сил?
9. Як визначаються величина та напрямок головного моменту довільної просторової системи сил?
10. Як виражається залежність головного моменту просторової системи сил від вибору центра зведення?
11. Що називають статичними інваріантами просторової системи сил?
12. Запишіть, як виражаються статичні інваріанти просторової системи сил.
13. Сформулюйте необхідну та достатню умову рівноваги довільної просторової системи сил.
14. Напишіть рівняння рівноваги довільної просторової системи сил.
15. Сформулюйте план розв’язання задачі на рівновагу невільного твердого тіла під дією довільної просторової системи сил.
16. Як записують рівняння рівноваги у випадку паралельних сил?
17. Які є випадки зведення просторової системи сил до найпростішого виду?
18. За яких умов дана система сил зводиться до пари сил та як обчислюється момент такої пари?
19. Коли дана система зводиться до рівнодіючої, яка проходить через центр зведення, та як обчислюється ця рівнодіюча?
20. За яких умов дана система зводиться до рівнодіючої, яка не проходить через центр зведення, а проходить через іншу точку?
21. Як обчислити відстань від точки прикладання рівнодіючої до центра зведення?
22. За яких умов дана система сил зводиться до динами?
23. Що називають віссю динами?
24. Запишіть рівняння центральної гвинтової осі.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 1838; Нарушение авторских прав?; Мы поможем в написании вашей работы!