
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Волны де Бройля. Вычислить дебройлевские длины электрона, протона и атома урана, имеющих кинетическую энергию эВ
|
|
|
|
5.86 [6.49]
Вычислить дебройлевские длины электрона, протона и атома урана, имеющих кинетическую энергию 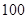 эВ.
эВ.
5.87 [6.50]
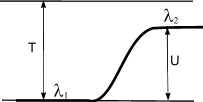 Частица движется слева направо в одномерном потенциальном поле, см. рис. Левее барьера, высота которого U = 15 эВ, кинетическая энергия частицы T = 20 эВ. Во сколько раз и как изменится дебройлевская длина волны частицы при переходе через барьер?
Частица движется слева направо в одномерном потенциальном поле, см. рис. Левее барьера, высота которого U = 15 эВ, кинетическая энергия частицы T = 20 эВ. Во сколько раз и как изменится дебройлевская длина волны частицы при переходе через барьер?
5.94 [6.57]
При каком значении кинетической энергии дебройлевская длина волны электрона равна его комтоновской длине волны.
5.96 [6.59]
Параллельный поток моноэнергетических электронов падает нормально на диафрагму с узкой прямоугольной щелью ширины b = 1,0 мкм. Определить скорость этих электронов, если на экране, отстоящем от щели на расстоянии l = 50 см, ширина центрального дифракционного максимума 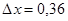 мм.
мм.
5.97 [6.60]
Параллельный поток электронов, ускоренных разностью потенциалов U = 25 B, падает нормально на диафрагму с двумя узкими щелями, расстояние между которыми d = 50 мкм. Определить расстояние между двумя соседними максимумами дифракционной картины на экране, расположенном на расстоянии
l = 100 см от щелей.
Соотношения (принцип) неопределённостей Гейзенберга
5.108 [6.71]
Оценить с помощью соотношения неопределённостей минимальную кинетическую энергию электрона, локализованного в области размером 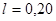 нм.
нм.
5.112 [ 6.75]
Частица массы m движется в одномерном потенциальном поле U = kx 2/2 (гармонический осциллятор). Оценить с помощью соотношения неопределённостей минимально возможную энергию частицы в таком поле.
5.113 [6.76]
Оценить с помощью соотношения неопределённостей минимально возможную энергию электрона в атоме водорода и соответствующее эффективное расстояние его от ядра.
Семинары 12, 13. Уравнение Шредингера. Частица в потенциальной яме. Потенциальный барьер. Туннельный эффект.
Волновая функция. Уравнение Шрёдингера. Потенциальная яма
5.123 [6.79]
Найти частное решение временного уравнения Шрёдингера для свободно движущейся частицы массы m.
5.124 [6.80]
Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Найти ширину ямы, если разность энергии между уровнями с n 1 = 2 и n 2 = 3 составляет
DЕ = 0,30 эВ.
5.125 [6.81]
Частица находится в основном состоянии в одномерной прямоугольной потенциальной яме ширины l c абсолютно непроницаемыми стенками (0< x < l). Найти вероятность пребывания частицы в области l/3< x <2 l /3.
5.129 [6.82]
Частица находится в одномерной потенциальной яме с бесконечно высокими стенками. Ширина ямы 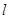 .Найти нормированные волновые функции стационарных состояний частицы, взяв начало отсчёта в середине ямы.
.Найти нормированные волновые функции стационарных состояний частицы, взяв начало отсчёта в середине ямы.
5.131 [6.85]
Частица массы m находится в двумерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками. Найти:
а) возможные значения энергии, если стороны ямы равны l 1 и l 2;
б) значения энергии частицы на первых четырех уровнях, если яма квадратная со стороной l.
5.138 [6.92]
Найти возможные значения энергии частицы массы 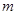 , находящейся в сферически-симметричной потенциальной яме
, находящейся в сферически-симметричной потенциальной яме 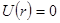 при
при 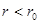 и
и 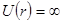 при
при 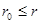 , для случая, когда движение частицы описывается волновой функцией
, для случая, когда движение частицы описывается волновой функцией 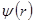 , зависящей только от
, зависящей только от 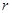 .
.
Указание. При решении уравнения Шрёдингера воспользоваться подстановкой 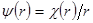 .
.
5.141 [6.95]
Волновая функция частицы массы m для основного состояния в одномерном потенциальном поле U(x)= kx 2/2 имеет вид y(x)=A exp (-ax2), где 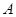 и
и 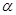 - некоторые постоянные. Найти с помощью уравнения Шредингера постоянную
- некоторые постоянные. Найти с помощью уравнения Шредингера постоянную 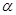 и энергию
и энергию 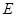 частицы в этом состоянии.
частицы в этом состоянии.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 2565; Нарушение авторских прав?; Мы поможем в написании вашей работы!