Закон стокса

Как известно, течение потоков жидкости (или газа) бывает ламинарным и турбулентным. Английский ученый Рейнольдс установил, что характер течения зависит от значения безразмерной величины: Re = 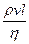, где ρ – плотность жидкости (или газа), – средняя скорость потока, – характерный геометрический параметр потока, – коэффициент вязкости жидкости (или газа). При больших значениях Re наблюдается турбулентное течение, а при малых – ламинарное.

При малых Re сопротивление среды обусловлено только силами трения. Стокс установил следующую закономерность: для тела, находящегося в ламинарном потоке, сила сопротивления среды пропорциональна коэффициенту динамической вязкости η, скорости ν движения тела относительно жидкости и характерному размеру тела l.

Если тело имеет сферическую форму, то сила сопротивления потока будет равна:

F_c=6πηrv.

Как и любая другая сила трения, Fc всегда направлена в сторону противоположную движению тела.

Решим некоторые типичные задачи по этой теме.

Задача 1: Какой диаметр должна иметь дождевая капля, чтобы достичь скорости

υ=45,4 м/с, если динамическая вязкость воздуха равна η=1,2·10^-5 Па·с? Плотность воды ρ=10³ кг/м³.

Дано:

υ=4,1 м/с Рассмотрим все силы, которые действуют на каплю в даннях условиях:

η=1,2·10^-5 Па·с 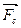Во-первых, это сила тяжести F_т, которая направлена

ρ=10³ кг/м³ всегда вертикально вниз. А во-вторых, это сила

сопротивления F_с, которая в данном случае направ-

d -? лена вертикально вверх (противоположно движению).

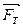Силу Архимеда (которая в данных условиях тоже имеет место) учитывать не будем вследствие ее малой величины.

Поскольку капля, в конце концов, приобретает определенную постоянную скорость, то эти две силы уравновешивают друг друга: = (*).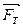

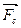В скалярном виде уравнение (*) имеет вид: F_т = F_с, где F_с = 6πηrυ

F_т = mg

g = 9,8 м/с² – ускорение свободного падения,

m = ρV – масса капли,

ρ – плотность воды,

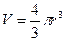- объем капли (согласно формуле объема шара).

Таким образом, F_т равно: F_т = .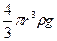

Уравнение (*) приобрело следующий вид: 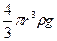= 6πηrυ

Решим его. Сократим на общий множитель 2πr: 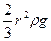= 3ηυ

Найдем r: r² = 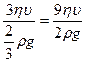; r = .

Для подтверждения правильности конечной формулы произведем действия с единицами измерений:

[r] = .

Вычислим r: r = .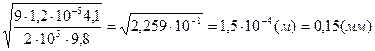

Теперь ответим на вопрос задачи: d = 2r; d = 2·1,5·10^-4=3·10^-4 (м) = 0,3 (мм).

Ответ: d = 0,3 мм.

Задача 2: Пробковый шарик радиусом 5 мм всплывает в сосуде, наполненном касторовым

маслом. Чему равны динамическая и кинематическая вязкости касторового

масла в условиях опыта, если шарик всплывает с постоянной скоростью

3,5 см/с? Плотность касторового масла равна 900 кг/м³. Плотность пробковой коры равна 150 кг/м³.

Дано: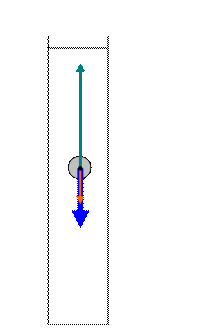

r=5мм=5·10^-3м Составим уравнение: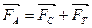

υ=3,5см/с=3,5·10^-2м

ρж=900кг/м³ 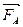В скалярном виде уравнение имеет вид:

ρ_Т=150 кг/м³.

η -? ν -? F_A=F_C+F_T

F_A=ρ_жgV_ш=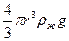

F_C=6πηrυ,

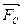F_T=mg= .

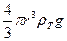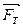Таким образом получаем уравнение, которое

нужно решить относительно η:

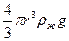= 6πηrυ+ ;

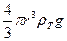6πηrυ= - ;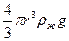

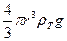6πηrυ = ;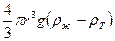

η= ;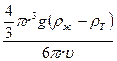

η = .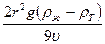

Для подтверждения правильности конечной формулы произведем действия с единицами измерений:

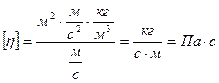
Найдем η: η= 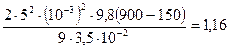(Па·с)

Найдем ν: ;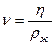

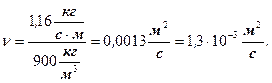
Ответ: η = 1,16 Па·с, ν = 1,3·10^-3 м²/с.

Задача 3: Смесь свинцовых дробинок діаметром d₁ = 3 мм и d₂ = 1 мм опустили в бак с гліцерином глубиной h = 1 м. На сколько позже упадут на дно дробинки меньшего діаметра по сравнению с дробинками большего диаметра? Динамическая вязкость при температуре опыта η = 1,47 Па·с, плотность свинца ρ_с = 11300 кг/м³, плотность глицерина ρ_г = 1200 кг/м³.

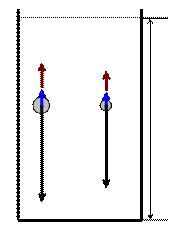
Дано:

d₁ = 3 мм = 3·10^{-3 м}

d₂ = 1 мм = 10^{-3 м}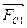

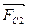
h = 1 м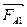

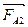
η = 1,47 Па·с h

ρ_с = 11300 кг/м³

ρ_г = 1200 кг/м³

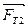
Δt -?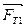

Δt = t₂ – t₁,

где t₁ – время, в течение которого упадут дробинки диаметром d₁,

t₂ – время, в течение которого упадут дробинки диаметром d₂.

Учитывая, что движение дробинок будет равномерным (вследствие уравновешивания сил), имеем:

; .

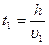Следовательно для решения этой задачи нужно найти υ₁ и υ₂.

Составим уравнение для дробинок диаметром d_1: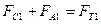

F_C1=6πηr₁υ₁;

F_A1=ρ_гgV_с= ;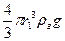

F_T1=m₁g= .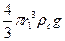

6πηr₁υ₁+ = ;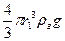

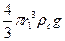6πηr₁υ₁= - ;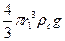

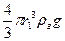6πηr₁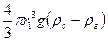υ₁= ;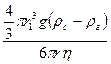

υ₁= ; υ₁= .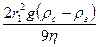

Очевидно, что для дробинок диаметром d₂ все выкладки будут призводиться аналогічно, в результате чего получаем:

υ₂= .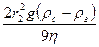

Произведем вычисления:

υ₁=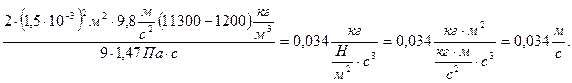

.

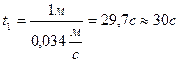υ₂=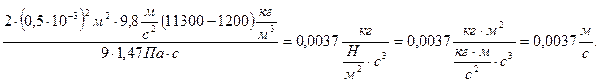

.

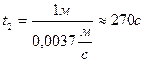Δt =270с – 30с = 240 с = 4 мин.

Ответ: Δt =4 мин

Дата добавления: 2015-06-04