Разложение силы по трем осям координат

Пространственная система сил

Условия равновесия пространственной системы сил.


Пространственная система сходящихся сил

Система сил, линии действия которых расположены в различных плоскостях, называется пространственной системой сил.

Пространственная система сил называется сходящейся, если линии действия всех сил системы пересекаются в одной точке.

Теорема: пространственная система сходящихся сил эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил.

Пусть дана пространственная система n сходящихся сил (F₁, F₂, F₃,....F_n). На основании следствия из аксиом III и IV перенесем все силы системы вдоль линий действия в точку их пересечения. Затем на основании аксиомы параллелограмма последовательно сложим все силы и получим их равнодействующую:

F_Σ = F₁ + F₂ + F₃ +....+ F_n, или F_Σ = ΣF_i.

Силовой многоугольник пространственной системы сил не лежит в одной плоскости, поэтому геометрический и графический способы нахождения равнодействующей пространственной системы сходящихся сил неприемлемы, а применяется только аналитический способ (метод проекций).

Проекция силы на ось в пространстве находится по проецирующим перпендикулярам, и может быть определена при помощи тригонометрических функций. При определении проекций сил пространственной системы потребуется система координат с осями X, Y, Z, поскольку силы системы не располагаются в одной плоскости.

Правило знаков для проекций будет таким же, как и для плоской системы сил – совпадающие по направлению с координатной осью силы считаются положительными, в противном случае – отрицательными. Если вектор силы параллелен какой-либо оси координат, то он проецируется на эту ось в натуральную величину, если же вектор перпендикулярен оси, его проекция на эту ось будет равна нулю.

Пусть дана сила F (см. рисунок 1).
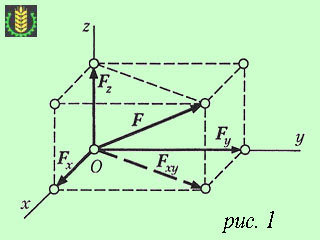Возьмем систему координат так, чтобы начало координат совпадало с началом вектора силы F (т. е. с точкой приложения силы). Из конца этого вектора опустим перпендикуляр на плоскость xy и разложим силу F на составляющие F_xy и F_z, а составляющую F_xy – на составляющие F_x и F_y. Тогда:

F = F_x + F_y + F_z.

Достроим полученное изображение до параллелепипеда, у которого составляющие F_x, F_y и F_z являются ребрами, а сила F – диагональю.

Из изложенного можно сделать вывод: равнодействующая трех взаимно-перпендикулярных сил выражается по модулю и направлению диагональю параллелепипеда, построенного на этих силах.

Из рисунка видно, что в случаях разложения силы F по трем взаимно-перпендикулярным направлениям x, y, z составляющие F_x, F_y и F_z равны по модулю проекциям силы F на эти оси.

Зная проекции силы на три взаимно-перпендикулярные оси координат, можно определить модуль и направление вектора силы по формулам:

модуль силы: F = √(F_x² + F_y² + F_z²) (здесь и далее √ - знак корня);

направляющие косинусы: cos(F,x) = Fx/F; cos(F,y) = Fy/F; cos(F,z) = Fz/F.

Дата добавления: 2015-06-04