
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Перпендикулярность прямых и плоскостей
|
|
|
|
 Две прямые называются перпендикулярными, ели они пересекаются под прямым углом.
Две прямые называются перпендикулярными, ели они пересекаются под прямым углом.
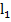
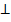
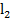
Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой в плоскости, проходящей через точку пересечения данной прямой и плоскости. 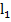
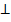
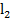
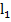
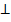 α
α 
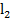 ϵ α
ϵ α
 Две плоскости называются перпендикулярными, если пересекаясь, они образуют прямые двугранные углы. α
Две плоскости называются перпендикулярными, если пересекаясь, они образуют прямые двугранные углы. α 
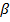
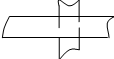
 Признак перпендикулярности прямой и плоскости. Если прямая, пересекающая плоскость, перпендикулярна двум пересекающимся прямым в этой плоскости, то она перпендикулярна плоскости.
Признак перпендикулярности прямой и плоскости. Если прямая, пересекающая плоскость, перпендикулярна двум пересекающимся прямым в этой плоскости, то она перпендикулярна плоскости.
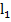
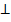 l
l
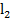
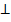 l l
l l 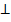 α
α
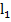 ∩
∩ 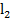
 Признак перпендикулярности двух плоскостей. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Признак перпендикулярности двух плоскостей. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Теоремы о перпендикулярных прямых и плоскостях:
1. 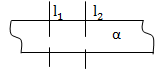 Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.  ǁ
ǁ 
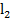
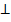 α
α
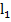
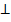 α
α
2. Если две прямые перпендикулярны одной и той же плоскости, то они параллельны.
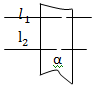

 α
α  ǁ
ǁ 
 α
α
3. 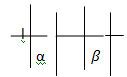 Если прямая перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и другой. α ǁ
Если прямая перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и другой. α ǁ  l
l 
l  α
α
4. Если две плоскости перпендикулярны одной и той же прямой, то они параллельны.
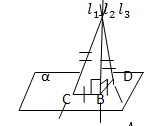 Перпендикуляр и наклонная
Перпендикуляр и наклонная 
 α
α
Теорема. Если из одной точки вне плоскости проведены  I
I 
 α
α
Перпендикуляр и наклонные, то:
1) Наклонные, имеющие равные проекции, равны;

2) Из двух наклонных больше та, проекция которой больше;
3) Равные наклонные имеют равные проекции;
4) Из двух проекций больше та, которая соответствует большей наклонной.
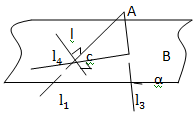 Теорема о трёх перпендикулярах. Для того чтобы прямая, лежащая в плоскости, была перпендикулярна наклонной, необходимо и достаточно, чтобы эта прямая была перпендикулярна проекции наклонной.
Теорема о трёх перпендикулярах. Для того чтобы прямая, лежащая в плоскости, была перпендикулярна наклонной, необходимо и достаточно, чтобы эта прямая была перпендикулярна проекции наклонной.
l ϵ α i  ∩ α=C
∩ α=C  ∩
∩  =A
=A

 α
α
 l
l 

Теорема о площади ортогональной проекции многоугольника на плоскость. Площадь ортогональной проекции многоугольника на плоскость равна произведению площади многоугольника на косинус угла между плоскостью многоугольника и плоскостью проекции.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 795; Нарушение авторских прав?; Мы поможем в написании вашей работы!