Постулат об измерении

Двумерное и трехмерное уравнение Шредингера. Стационарное уравнение Шредингера.

Как мы уже видели, предсказания квантовой теории носят вероятностный характер. Выясним, когда измерение наблюдаемой 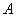дает определенный результат. Рассмотрим отклонение от среднего . Ему отвечает наблюдаемая , где 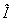- единичный оператор (в дальнейшем его будем опускать). Дисперсия случайной переменной 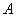в состоянии 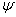равна 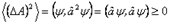. Она обращается в нуль только пр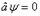и , или .
Следовательно, в указанном состоянии наблюдаемая имеет определенное значение, которое совпадает с одним из собственных значений оператора наблюдаемой. Само состояние описывается волновой функцией, представляющей собой собственный вектор оператора.

В дальнейшем для краткости, если это не приведет к недоразумению, мы будем отождествлять понятия состояния и соответствующей ему волновой функции (используется также термин вектор состояния), наблюдаемой и оператора наблюдаемой.

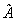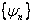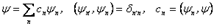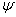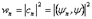Пусть наблюдаемая имеет дискретный спектр: , причем система собственных функций полна и ортонормированна, т.е. образует базис в пространстве состояний: .Здесь - произвольный вектор с единичной нормой. Имеем следующие соотношения: . Отсюда следует, что есть вероятность получить значение наблюдаемой 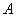при измерении в состоянии 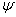, причем значений на опыте обнаружить нельзя.

Если наблюдаемая 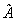имеет непрерывный спектр , то 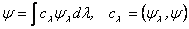.Тогда 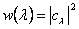- плотность вероятности, т.е. 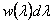- вероятность обнаружить значение 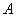в интервале 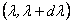. При этом . Условие ортонормированности заменяется условием нормировки на 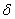-функцию: .

Дата добавления: 2015-06-04