Вторая аксиома

Две силы, равные по модулю и направленные по одной прямой в разные стороны, уравновешиваются (рис. 1.2). Рис. 1.2

Третья аксиома

Не нарушая механического состояния тела, можно добавить или убрать уравновешенную систему сил (принцип отбрасывания систе­мы сил, эквивалентной нулю) (рис. 1.3).

¹⁾ Векторные величины обозначаются полужирным шрифтом, скалярные величины – обычным.

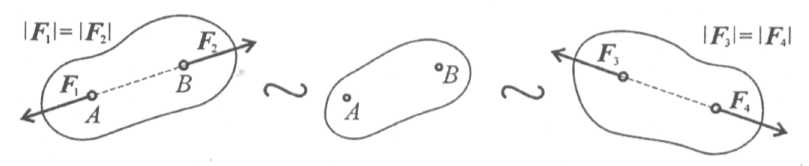
Рис. 1.3

Четвертая аксиома (правило параллелограмма сил)

Равнодействующая двух сил, прило­женных в одной точке, приложена в той же точке и является диагональю паралле­лограмма, построенного на этих силах как на сторонах (рис. 1.4).

Вместо параллелограмма можно по­строить треугольник сил: силы вычерчи­вают одну за другой в любом порядке; равнодействующая двух сил соединяет начало первой силы с концом второй.

Пятая аксиома

При взаимодействии тел всякому действию соответствует равное и противоположно направленное противодействие (рис. 1.5).

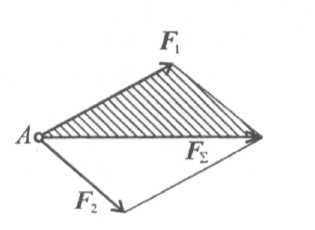
Рис. 1.4

Силы действующие и противо­действующие всегда приложены к разным телам, поэтому они не урав­новешиваются.

Силы, с которыми два тела дей­ствуют друг на друга, всегда равны
по модулю и направлены вдоль одной прямой в разные стороны.

Рис. 1.5

Следствие из второй и третьей аксиом

Силу, действующую на твер­дое тело, можно перемещать вдоль линии ее действия (рис. 1.6).

Сила F приложена в точ­ке А. Требуется перенести ее в точку В. Используя третью аксиому, добавим в точке (F’; F”). Образуется уравнове­шенная по второй аксиоме систе­ма сил (F; F”). Убираем ее и получим в точке В силу F", равную заданной F.

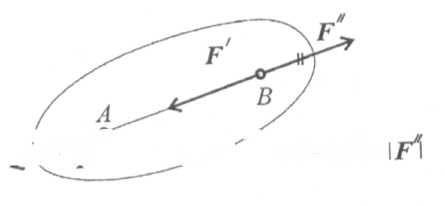
Рис. 1.6

^ Связи и реакции связей

Все законы и теоремы статики справедливы для свободного твердого тела.

Все тела делятся на свободные и связанные.

Свободные тела — тела, перемещение которых не ограничено.

Связанные тела — тела, перемещение которых ограничено дру­гими телами.

^ Тела, ограничивающие перемещение других тел, называют свя­зями.

Силы, действующие от связей и препятствующие перемещению, называют реакциями связей.

Реакция связи всегда направлена с той стороны, куда нельзя перемещаться.

^ Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей).

Все связи можно разделить на несколько типов.

Связь — гладкая опора (без трения)

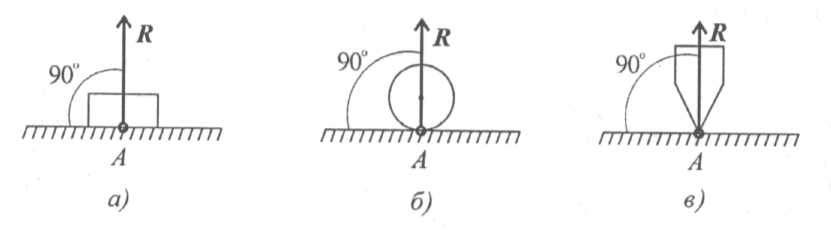
Рис. 1.7

Реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре (рис. 1.7).

Гибкая связь (нить, веревка, трос, цепь)

Груз подвешен на двух нитях (рис. 1.8).

Реакция нити направлена вдоль нити от ела, при этом нить может быть только растянута.

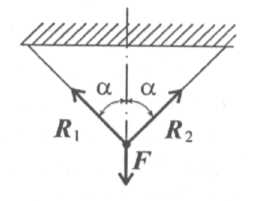
Рис. 1.8

Жесткий стержень

На схемах стержни изображают толстой сплошной линией (рис. 1.9).

Стержень может быть сжат или растянут. Ре­акция стержня направлена вдоль стержня. Стер­жень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения те­ла без этой связи.

^ Возможным перемещением точки называется такое бесконечно малое мысленное перемещение, которое допуска­ется в данный момент наложенными на него связями.

Убираем стержень 1, в этом случае стержень 2 падает вниз. Сле­довательно, сила от стержня 1 (реакция) направлена вверх. Убираем стержень 2. В этом случае точка Л опускается вниз, отодвигаясь от стены. Следовательно, реакция стержня 2 направлена к стене.

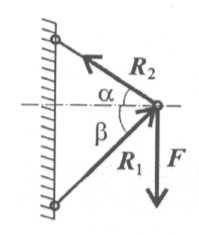
Рис. 1.9

Шарнирная опора

Шарнир допускает поворот вокруг точки закрепления. Различа­ют два вида шарниров.

Подвижный шарнир

Стержень, закрепленный на шарнире, может поворачивать­ся вокруг шарнира, а точка крепления может перемещаться вдоль направляющей (площадки) (рис. 1.10).

Рис. 1.10

Реакция подвижного шарни­ра направлена перпендикулярно опорной поверхности, т. к. не до­пускается только перемещение поперек опорной поверхности.

Неподвижный шарнир

Точка крепления пере­мещаться не может. Стер­жень может свободно повора­чиваться вокруг оси шарни­ра. Реакция такой опоры про­ходит через ось шарнира, но неизвестна по направлению. Ее принято изображать в ви­де двух составляющих: гори­зонтальной и вертикальной (R_x\Ry) (рис. 1.11).

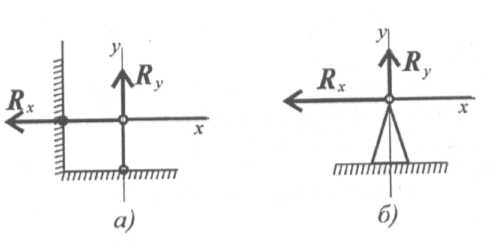
Рис. 1.11

Защемление или «заделкам

Рис. 1.12

Любые перемещения точки крепле­ния невозможны.

Под действием внешних сил в опоре возникают реактивная сила и реактив­ный момент Mr, препятствующий пово­роту (рис. 1.12).

Реактивную силу принято предста­влять в виде двух составляющих вдоль осей координат

R = R_x + R_y.

Контрольные вопросы и задания

1. Какая из приведенных систем сил (рис. 1.13) уравновешена?

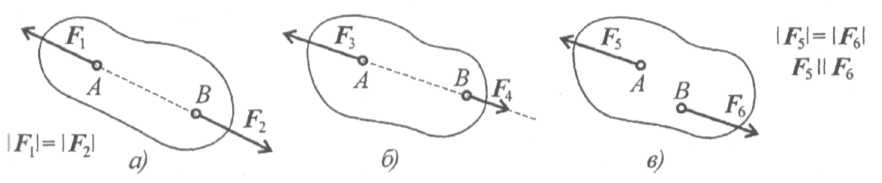
Рис. 1.13

2. Какие силы системы (рис. 1.14) можно убрать, не нарушая механического состояния тела?

Рис.1.14

3. Тела 1 и 2 (рис. 1.15) находятся в равновесии. Можно ли убрать действующие системы сил, если тела абсолютно твердые? Что изменится, если тела реальные, деформируемые?

Рис. 1.15

4. Укажите возможное направление реакций в опорах (рис. 1.16).

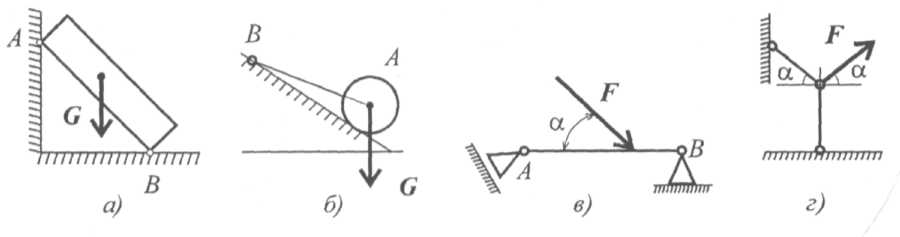
Рис. 1.16

Дата добавления: 2015-06-04