Произвольная пространственная система сил

Если силы, действующие на тело, лежат в пространстве, то такая система сил называется пространственной, и если главный вектор и главный момент системы равны нулю, то система сил уравновешенная.

Следовательно, необходимые и достаточные условия равновесия пространственной системы будут R = 0, M = 0 - в векторной форме. Так как при равновесии главный момент нравен нулю относительно любого центра приведения, то вместо 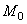можно писать М без индекса.

Спроектировав главный вектор R на координатные оси Оx, Оy, Оz получим аналитические условия равновесия произвольной пространственной системы сил, которые выражаются шестью уравнениями равновесия и

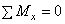
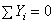
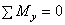(28)

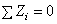
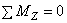
и формулируется так: произвольная пространственная система сил находится в равновесии, если сумма проекций сил на каждую из координатных осей и сумма моментов всех сил относительно осей координат равны нулю.

При решении необходимо рассмотреть связи, которые до сих пор не встречались нам.

Подпятник (рис.38) - это тип опоры не препятствующий повороту тела или какой-либо его детали вокруг своего центра, но препятствующий смещению тела в любом направлении, поэтому для такого типа опоры не известны ни величина реакции, ни образуемые его с координатами осями углы, а известна только точка приложения реакции.

Рис. 38

Такую реакцию можно представить составляющими, направленными в положительных направлениях трех осей координат (отрицательный знак, полученный при решении уравнения равновесия, покажет, что в действительности та или иная составляющая опорной реакции направлена в противоположную выбранному направлению сторону).

В большинстве задач требуется определить не реакцию, а ее составляющие, сама реакция определяется как диагональ прямоугольного параллепипеда, построенного на составляющих X, Y, Z как на сторонах.

.

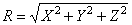Направление реакции можно определить по направляющим косинусам

,

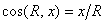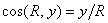, (29)

.

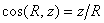Подлинник (рис.39) - это цилиндрический шарнир, позволяющий телу или его элементу (например, валу, оси и т.д.) поворачиваться вокруг своей оси, смещаться вдоль нее, но не позволяющему перемещаться в перпендикулярной плоскости к его оси, следовательно, реакция подшипника может быть расположена только в плоскости, перпендикулярной к его оси. Зная в этой плоскости только точку приложения реакции и не зная угла, образуемого его с какой-либо находящейся в этой плоскости осью, представляем реакцию двумя составляющими, направленными в положительные стороны координатных осей, расположенных в этой плоскости. Сама реакция R может быть определена как равнодействующая определенных составляющих Z и Y.

Рис.39

. (30)

Направление ее может быть найдено по формулам:

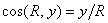, (31)

.

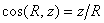Для равновесия любой плоской системы сил необходимо и достаточно, чтобы выполнялись условия (4.2.5):

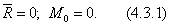
Записывая условия равновесия в аналитической форме, можно привести три их классических вида:

1. Основная форма условий равновесия:

Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций на оси координат были равны нулю и сумма моментов всех сил относительно центра О была равна нулю.

2. Вторая форма условий равновесия.

Для равновесия произвольной плоской системы необходимо и достаточно, чтобы сумма моментов относительно двух произвольно взятых точек тела была равна нулю и сумма проекций сил на одну из осей координат была равна нулю:

6) Основные понятия кинематики. Способы задания движения точки.
Кинематикой называют раздел теоретической механики, в котором изучается движение материальных тел с геометрической точки зрения незави­симо от приложенных сил.

Положение движущегося тела в пространстве всегда определяется по отношению к любому другому неизменяемому телу, называемому телом отсчета. Система координат, неизменно связанная с телом отсчета, называется системой отсчета. В механике Ньютона время считается абсолютным и не связанным с движущейся материей. В соответствии с этим оно протекает одинаково во всех системах отсчета независимо от их движения. Основной единицей измерения времени является секунда (с).

Если положение тела по от­ношению к выбранной системе отсчета с течением времени не изменяется, то говорят, что тело относительно данной системы отсчета находится в покое. Если же тело изменяет свое положение относительно выбранной системы от­счета, то говорят, что оно движется по отношению к этой системе. Тело может находиться в состоянии покоя по отношению к одной системе отсчета, но дви­гаться (и притомсовершенно различным образом) по отношению к другим сис­темам отсчета. Например, пассажир, неподвижно сидящий на скамье движуще­гося поезда, покоится относительно системы отсчета, связанной с вагоном, но движется по отношению к системе отсчета, связанной с Землей. Точка, лежа­щая на поверхности катания колеса, движется по отношению к системе отсчета, связанной с вагоном, по окружности, а по отношению к системе отсчета, свя­занной с Землей, по циклоиде; та же точка покоится по отношению к систе­ме координат, связанной с колесной парой.

Таким образом, движение или покой тела могут рассматриваться лишь по от­ношению к какой-либо выбранной системе отсчета. Задать движение тела отно­сительно какой-либо системы отсчета - значит дать функциональные зависи­мости, с помощью которых можно определить положение тела в любой момент времени относительно этой системы. Различные точки одного и того же тела по отношению к выбранной системе отсчета движутся по-разному. Например, по отношению к системе, связанной с Землей, точка поверхности ката­ния колеса движется по циклоиде, а центр колеса - по прямой. Поэтому изучение кинема­тики начинают с кинематики точки.

Способы задания движения точки

Движение точки может быть задано тремя способами: естественным, векторным и координатным.

При естественном способе задания движения дается траектория, т. е. линия, по которой движется точка (рис.2.1). На этой траектории выбирается некоторая точка 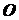, принимаемая за начало от­счета. Выбираются положительное и отрицательное направления отсчета дуговой координаты 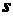, определяющей положение точки на траектории. При движе­нии точки расстояние 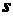будет изменяться. Поэтому, чтобы определить положение точки в любой момент времени, достаточно задать дуговую коор­динату 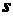как функцию времени:

. (2.1)

Это равенство называется уравнением движения точки по данной траектории.

Итак, движение точки в рассматриваемом случае определяется совокупностью следующих данных: траектории точки, положения начала отсчета дуговой координаты, положительного и отрицательного направлений отсчета и функции .

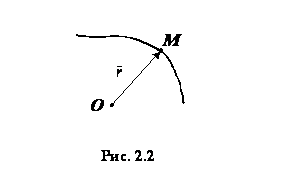При векторном способе задания движения точки положение точки определя­ется величиной и направлением радиуса-вектора 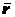, проведенного из неподвиж­ного центра 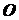в данную точку (рис. 2.2). При движении точки ее радиус-вектор 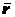изменяется по величине и направлению. Поэтому, чтобы оп­ределить положе­ние точки в любой момент времени, достаточно задать ее радиус-вектор 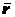как функцию времени:

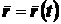. (2.2)

Это равенство называется векторным уравнением движения точки.

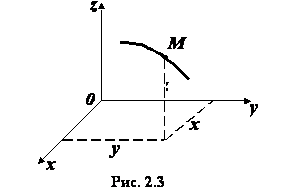При координатном способе задания движения положение точки по отношению к выбранной системе отсчета определяется при помощи прямоугольной системы декартовых координат (рис. 2.3). При движении точки ее координаты изменяются с течением времени. Поэтому, чтобы определить положение точки в любой момент времени, достаточно задать координаты 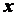, , 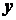как функции времени:

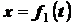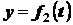; ; . (2.3)

Эти равенства называются уравнениями движения точки в прямоугольных де­картовых координатах. Движение точки в плоскости определяется двумя уравне­ниями системы (2.3), прямолиней­ное дви­жение — одним.

Между тремя описанными способами задания движения существует вза­имная связь, что позволяет от одного способа задания движения перейти к другому. В этом легко убедиться, например, при рассмотрении перехода от ко­ординатного способа задания движения к векторному.

Положим, что движение точки задано в виде уравнений (2.3). Имея в виду, что и ; ; 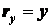, можно записать

.

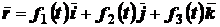А это и есть уравнение вида (2.2).

7) Определение скоростей и ускорений точек тела при естественном и координатном способах задания движения
Вектор скорости точки

Одной из основных кинематических характеристик движе­ния точки является векторная величина, называемая скоростью точки.

Скорость - мера механического состояния тела. Она характеризует быстроту изменения положения тела относительно данной системы отсчета и является векторной физической величиной.

Единица измерения скорости – м/с. Часто используют и другие единицы, например, км/ч: 1 км/час=1/3,6 м/с.

Известно, что при движении точки по прямой линии с постоянной скоростью, равномерно, скорость её определяется делением пройденного расстояния s на время: 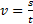. При неравномерном движении эта формула не годится. Введем сначала понятие о средней скорости точки за какой-нибудь промежуток времени.

Пусть движущаяся точка находится в момент времени t в положении М, определяемом радиусом-векто­ром 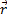, а в момент t₁ приходит в положение M ₁ определяемое векто­ром (рис.7). Тогда перемещение точки за промежуток времени ∆t=t₁-t определяется вектором который будем называть вектором перемещения точки. Из треугольника ОММ ₁ видно, что 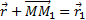; следовательно,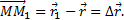

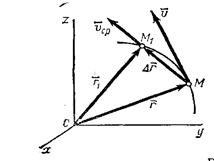
Рис. 7

Отношение вектора перемещения точки к соответствующему промежутку времени дает векторную величину, называемую сред­ней по модулю и направлению скоростью точки за промежуток времени ∆t:

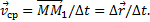
Скоростью точки в данный момент времени t называется векторная величина v, к которой стремится средняя скорость v_ср при стремлении промежутка времени ∆t к нулю:

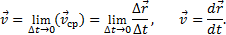
Итак, вектор скорости точки в данный момент времени равен первой производной от радиуса-вектора точки по времени.

Так как предельным направлением секущей ММ ₁ является касательная, то вектор скорости точки в данный момент времени направлен по касательной к траектории точки в сторону движения.

Определение скорости точки при координатном способе задания движения

Вектор скорости точки , учитывая, что r_x=x, r_y=y, r_z=z, найдем:

Таким образом, проекции скорости точки на координатные оси равны первым производным от соответствующих координат точки по времени.

Зная проекции скорости, найдем ее модуль и направление (т.е. углы α, β, γ, которые вектор v образует с координатными осями) по формулам

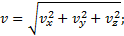
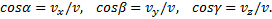
Итак, численная величина скорости точки в данный момент времени равна первой производной от расстояния (криволинейной координаты) s точки по времени.

Направлен вектор скорости по касательной к траектории, кото­рая нам наперед известна.

Определение скорости точки при естественном способе задания движения

Величину скорости можно определить как предел (∆r – длина хорды ММ ₁):

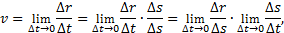
где ∆s – длина дуги ММ ₁. Первый предел равен единице, второй предел – производная ds/dt.

Следовательно, скорость точки есть первая производная по времени от закона движения:

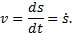
Направлен вектор скорости, как было установлено ранее, по касательной к траектории. Если величина скорости в данный момент будет больше нуля, то вектор скорости направляется в положительном направлении

Дата добавления: 2015-06-04