
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Эллипсоид
|
|
|
|
Конус
Эллипсоид деп мынадай
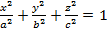 (15)
(15)
теңдеуімен анықталатын геометриялық бетті айтамыз. Бұл теңдеуді қарастырудан бұрын мына мәселеге тоқталайық. Кеңістіктегі геометрияда айналмалы геометриялық беттер жиі кездеседі. Мысалы: айналмалы цилиндр, айналмалы конус немесе айналмалы эллипсоид. Қысқаша айтқанда, айналмалы екінші ретті бет дегеніміз не?
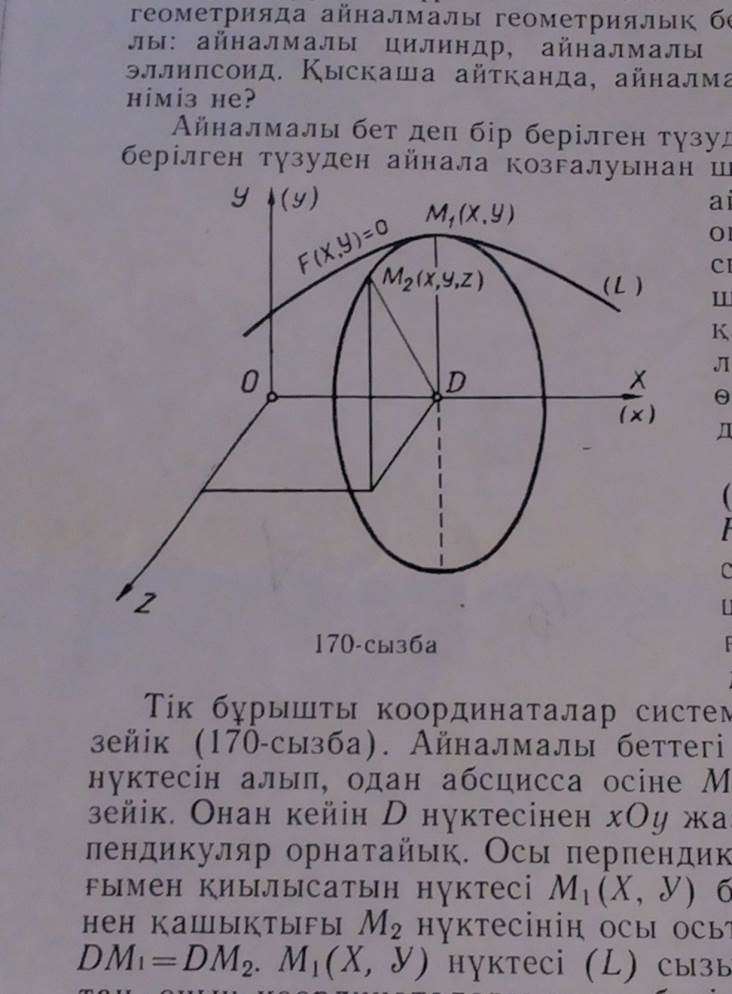 Айналмалы бет деп бір берілген түзудің немесе қисық сызықтың берілген түзуден айнала қозғалуынан шыққан бетті айтамыз. Бұл айналмалы бет қозғалғанда, оның әрбір нүктесі шеңбер сызады. Берілген түзу сол шеңбердің жазықтығына әрқашанда перпендикуляр болады және оның центрінен өтеді. Бұл түзу айналу осі деп аталады.
Айналмалы бет деп бір берілген түзудің немесе қисық сызықтың берілген түзуден айнала қозғалуынан шыққан бетті айтамыз. Бұл айналмалы бет қозғалғанда, оның әрбір нүктесі шеңбер сызады. Берілген түзу сол шеңбердің жазықтығына әрқашанда перпендикуляр болады және оның центрінен өтеді. Бұл түзу айналу осі деп аталады.
xOy жазықтығында бір (L) сызығы бізге мынадай F(X, Y)=0 теңдеуімен берілсін.Осы (L) сызығының абсцисса осінен айналғанда шығатын беттің теңдеуін іздейік.
Тік бұрышты координаталар системасына (L) сызығын жүргізейік (170-сызба). Айналмалы беттегі кез-келген бір M2(x, y, z) нүктесін алып, одан абцисса осіне M2D перпендикулярын жүргізейік. Онан кейін D нүктесінен xOy жазықтығындағы Ox осіне перпендикуляр орнатайық. Осы перпендикулярдың берілген (L) сызығымен қиылысатын нүктесі M1(X, Y) болсын. Бұл нүктенің Ox осінен қашықтығы M2 нүктесінің осы осьтен қашықтығындай болады: DM1=DM2. M1(X, Y) нүктесі (L) сызығының бойында жатқандықтан, оның координаталары мына берілген F(X, Y)=0 теңдеуін қанағаттандырады: M1D=ǀYǀ, M2D=  , M1D=DM2, ǀYǀ=
, M1D=DM2, ǀYǀ=  . Сондықтан
. Сондықтан
Y = + 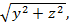 Y = -
Y = - 
M1, M2, D - нүктелері yOx жазықтығына параллель жазықтықта жатқандықтан, x = X.
Ендеше, мына F(X, Y)=0 теңдеуіндегі X пен Y- тің орнына X = x, Y =  , Y =
, Y = 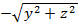 қойып, мынаны табамыз:
қойып, мынаны табамыз:
F(x,  ) = 0,
) = 0,
F(x, 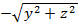 ) = 0
) = 0
Немесе
F(x, 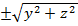 ) = 0. (16)
) = 0. (16)
Сөйтіп, XOY жазықтығындағы F(x, y) теңдеуімен берілген бір (L) сызығы OX осінен айналса, онда айналмалы беттің теңдеуі мынандай болады:
F(x, 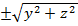 ) = 0,
) = 0,
Мұндағы x, y, z – кеңістіктегі нүктенің координаталары, Ox осі OX осімен, Oy осі OY осімен үйлеседі.
1-мысал. Түзудің xOy жазықтығында y = x теңдеуі берілсін. Егер осы түзуді Ox осінен айналдырсақ, онда (16) формула бойынша мынадай теңдеу шығады:
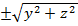 =x
=x
немесе
y2 +z2 = x2
y2 +z2 – x2 =0
Бұл-төбесі координаталардың бас нүктесінде жатқан конустық беттің теңдеуі. Сонымен, y = x биссектрисасының абсцисса осінен айналғаннан шыққан кеңістіктегі геометриялық бейнесі конус болады. Оның теңдеуі y2 +z2 – x2 =0.
2-мысал. Егер xOy жазықтығындағы x2+ y2 =R2 шеңберін абсйисса осінен айналдырсақ, онда айналмалы бет сфера болады. Оның теңдеуі 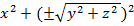 = R2 формуласы бойынша былай жазылады:
= R2 формуласы бойынша былай жазылады:
x2+y2 +z2 = R2
Егер 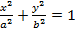 , z=0 эллипсті Ox осінен айналдырсақ, онда
, z=0 эллипсті Ox осінен айналдырсақ, онда
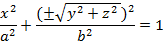
Немесе

Бұл айналмалы эллипсоид деп аталады. Егер осы айналмалы эллипсоидты y осінің бойымен созсақ, онда Y =  немесе y’=
немесе y’=  Y болады. Мұндағы b
Y болады. Мұндағы b 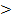 c – кесінділер. Айналмалы эллипсоидтың теңдеуі
c – кесінділер. Айналмалы эллипсоидтың теңдеуі  болсын.
болсын.
Енді y’ -тің мәнін осы теңдеуге қойып  эллипсоидтың теңдеуін табайық:
эллипсоидтың теңдеуін табайық:
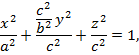
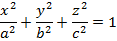
Егер  болса немесе үш ось 2a, 2b, 2c өз ара тең болмаса, онда эллипсоид үш осьтік эллипсоид деп аталады. Егер a=c немесе a=b болса, онда айналмалы эллипсоид болады. Егер a=b=c болса, онда эллипсоид шарға айналады.
болса немесе үш ось 2a, 2b, 2c өз ара тең болмаса, онда эллипсоид үш осьтік эллипсоид деп аталады. Егер a=c немесе a=b болса, онда айналмалы эллипсоид болады. Егер a=b=c болса, онда эллипсоид шарға айналады.
Эллипсоидтың координаталар осьтерімен қиылысатын нүктелері оның төбелері деп аталады. Ол нүктелер: A2(-a, 0, 0), A1(a, 0, 0), C2(0, 0, -c), C1(0, 0, c), B2(0, b, 0), B1(0, -b, 0). Төбелерінің арасындағы A1A2=2a, B1B2=2b, C1C2=2c кесінділері эллипсоидтың осьтері деп аталады (171-сызба).
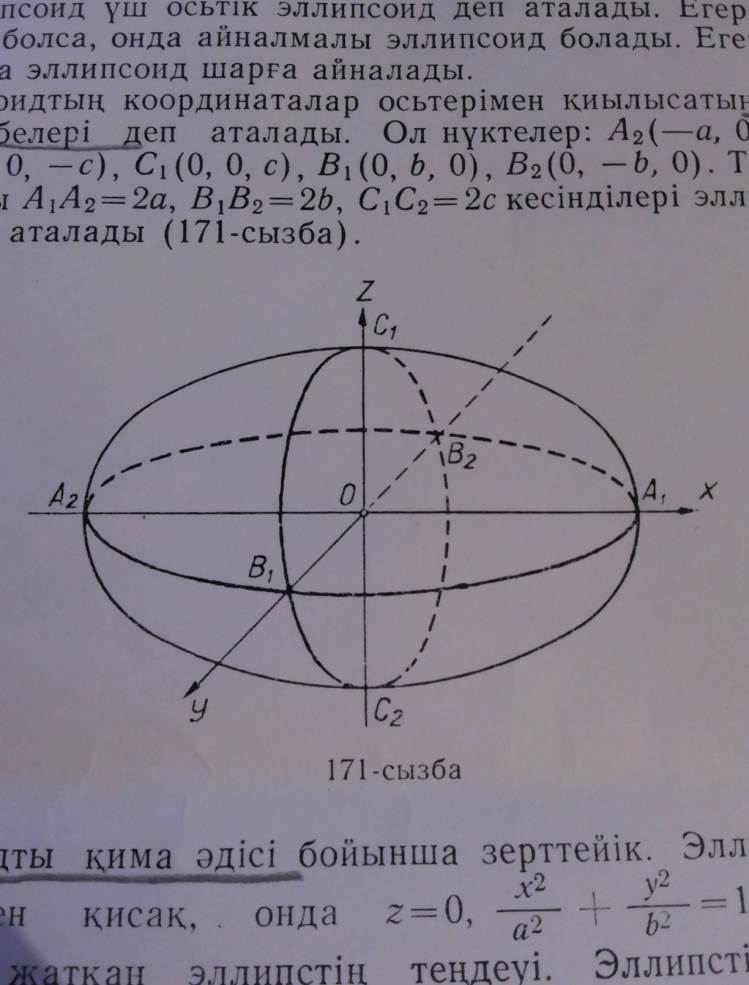
Эллипсоидты қима әдісі бойынша зерттейік. Эллипсоидты жазықтығымен қисақ, онда z=0, 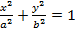 . Бұл xy жазықтығында жатқан эллипстің теңдеуі. Эллипсті мына z=h, z=-h жазықтықтарымен қисақ, онда
. Бұл xy жазықтығында жатқан эллипстің теңдеуі. Эллипсті мына z=h, z=-h жазықтықтарымен қисақ, онда
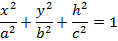
теңдеуі шығады.
Осы теңдеуді түрлендірейік:

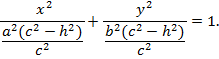
Бұл – xOy жазықтығына параллель z=±h жазықтығындағы эллипстің теңдеуі. Оның жарты осьтері: a1 = 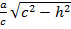 , b1 =
, b1 = 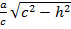 .
.
Сонымен,
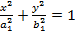 теңдеуі эллипсоидтың қимасын анықтайды. h өскен сайын, яғни z
теңдеуі эллипсоидтың қимасын анықтайды. h өскен сайын, яғни z 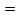 ±h жазықтықтары xOy жазықтығынан қашықтаған сайын эллипстің жарты осьтері кішірейе түседі. Ал h=c болғанда, жарты осьтер нольге тең: a1=b1=0, (0, 0, +c).
±h жазықтықтары xOy жазықтығынан қашықтаған сайын эллипстің жарты осьтері кішірейе түседі. Ал h=c болғанда, жарты осьтер нольге тең: a1=b1=0, (0, 0, +c).
Егер z=h болса,онда қима xOy жазықтығының жоғарғы жағында, егер z=-h болса, онда қима xOy жазықтығының төменгі жағында жатады. Егер (h)>c болса, онда 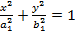 теңдеуі x пен y –тің ешбір нақты мәндерімен қанағаттанбайды, яғни бұл жағдайда z=±h жазықтығы эллипсоидты қимайды. Эллипсоидты жазықтарымен x=±h, y=±h қисақ та, қорытынды жоғары айтылғандай болады. Сөйтіп, эллипсоидтың қималары эллипс болады. Координаталар жазықтықтарындағы қималар эллипсоидтың бас қималары деп аталады.
теңдеуі x пен y –тің ешбір нақты мәндерімен қанағаттанбайды, яғни бұл жағдайда z=±h жазықтығы эллипсоидты қимайды. Эллипсоидты жазықтарымен x=±h, y=±h қисақ та, қорытынды жоғары айтылғандай болады. Сөйтіп, эллипсоидтың қималары эллипс болады. Координаталар жазықтықтарындағы қималар эллипсоидтың бас қималары деп аталады.
Егер эллипсоидтың бетіндегі бір нүктесі берілсе, онда осы нүктеден эллипсоидты жанап өтетін жазықтықтың теңдеуі мынадай болады:
 (17)
(17)
Мұны қорытып шығару үшін эллипсоидтың теңдеуін былай жазайық:
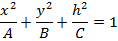
Мына
x=x1+lt,
y=y1+lt,
z=z1+nt
параметрлік теңдеулеріндегі координаталары жоғарғы берілген нүктесінің координаталары болсын. Сонда 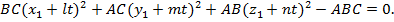
Осыдан мынадай квадрат теңдеу шығады:
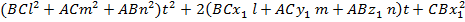 +AC
+AC 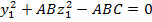 (A)
(A)
Бұл теңдіктің екі жағын ABC –ға бөлсек, онда
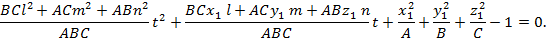
Квадрат теңдеудің түбірлері бірдей болу үшін мына шарт орындалады:
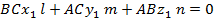
Енді
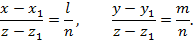
Бұл теңдеулерді пайдаланып, параметрлерін шығарып тастап, іздеген жанама жазықтықтың теңдеуін табайық:
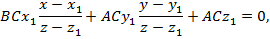
BCx 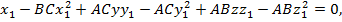

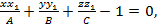 (15’)
(15’)
Мұндағы: A=a2, B=b2, C=c2.
§29. Бір қуысты гиперболоид
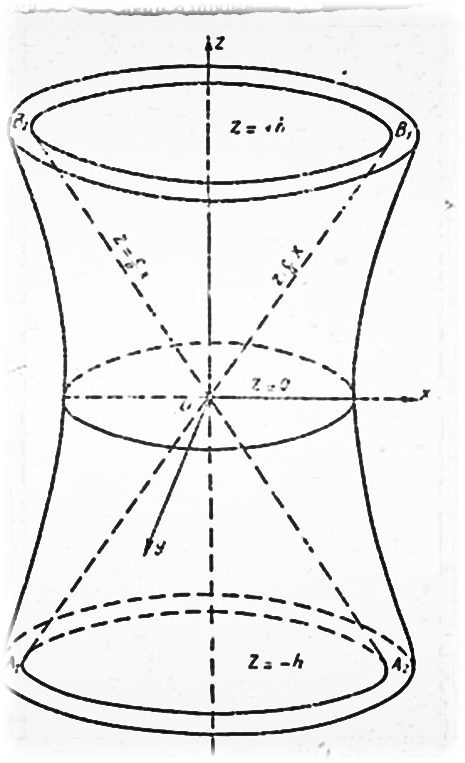 хОz жазықтығында
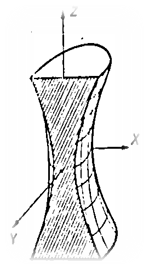
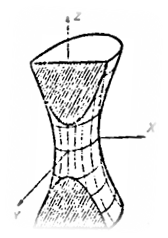
хОz жазықтығында 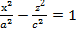 гипербола берілсін. Осы гиперболаны апликата осінен айналдырсақ, онда айналмалы бір қуысты гиперболоид деп аталатын геометриялық бет шығады (172-сызба). 4-параграфтағы (16) формула бойынша айналмалы бір қуысты гиперболоидтың теңдеуі мынадай болады:
гипербола берілсін. Осы гиперболаны апликата осінен айналдырсақ, онда айналмалы бір қуысты гиперболоид деп аталатын геометриялық бет шығады (172-сызба). 4-параграфтағы (16) формула бойынша айналмалы бір қуысты гиперболоидтың теңдеуі мынадай болады:
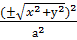 -
-  = 1
= 1
Осыдан
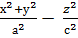 = 1 (18)
= 1 (18)
Берілген 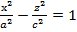 гиперболасының асимптоталары
гиперболасының асимптоталары 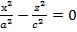 апликата осінен айналғанда
апликата осінен айналғанда
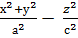 = 0
= 0
конус шығады. Мұны айналмалы бір қуысты гиперболоидтың асимптоталық конусы деп атаймыз. Бұл асимптоталық конустың жасаушылары бір қуысты гиперболоидпен шексіз алыстағы нүктелерде кездеседі.
Асимптоталардың теңдеулері 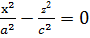 немесе
немесе 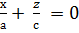 ,
, 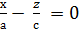 ,
,
z = 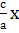 , z = -
, z = - 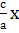 172-сызбада көрсетілген.
172-сызбада көрсетілген.
Егер z = 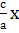 асимптотаны z осінен айналдырсақ, онда асимптоталық конус шығады:
асимптотаны z осінен айналдырсақ, онда асимптоталық конус шығады:
z =  (
(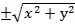 ),
), 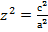 (
(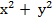 ),
),
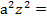
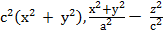 = 0.
= 0.
Бұл асимптоталық конус 172-сызбада А1В1А2В2 деп белгіленген.
Егер айнымалы бір қуысты гиперболоидты  = 1 Оу осінің бағытымен созсақ, онда бір қуысты гиперболоидтың теңдеуі мынадай болады:
= 1 Оу осінің бағытымен созсақ, онда бір қуысты гиперболоидтың теңдеуі мынадай болады:
 = 1 (19)
= 1 (19)
Бұл теңдеуді дәлелдеп шығарайық. Айналмалы бір қуысты гиперболоидты Оу осінің бағытымен созсақ, онда у-тің мәні бұрынғыға қарағанда өзгеріледі, яғни у′= kу. Бұл теңдіктегі k =  - пропорционалдық коэффицент, сонда у′ =
- пропорционалдық коэффицент, сонда у′ =  у. Айналмалы бір қуысты гиперболоидтың теңдеуін былайша жазайық:
у. Айналмалы бір қуысты гиперболоидтың теңдеуін былайша жазайық:
 = 1
= 1
Осыған у′-тің мәнін қояйық:
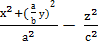 = 1,
= 1,
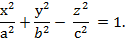
Бір қуысты гиперболоидтың тік бұрышты координаталар жүйесіндегі қималарының қандай болатынын теңдеуі арқылы тексерейік. хОу жазықтығына параллель z=һ жазықтығын жүргізсек, онда бір қуысты гиперболоидтың қимасы эллипс болады:
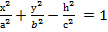 ,
,  =
= 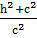 ,
,
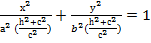 ,
, 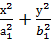 =1,
=1,
мұндағы а1=а 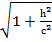 , b1=b
, b1=b 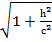 .
.
һ=z-тің абсолют мәні өскен сайын эллипстің жарты осьтері а1,b1 өсіп отырады, яғни һ=z өсуімен байланысты эллипс те кемиді. Һ нольге тең болғанда (һ=0,z=0), бір қуысты гиперболоидтың ең кішкене қимасы мынадай эллипстің теңдеуі болады:
 = 1.
= 1.
Сонымен, бір қуысты гиперболоидтың хОу жазықтығындағы ең кішкене қимасы z=0 координаталардың бас нүктесінен өтеді (172-сызбаға қараңыз).
 Бір қуысты гиперболоидты уz жазықтығымен қияйық, яғни х=0 болса, онда
Бір қуысты гиперболоидты уz жазықтығымен қияйық, яғни х=0 болса, онда 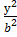 -
-  =1 болады. Бұл - уz жазықтығында жатқан гиперболаның теңдеуі. Мұның нақты осі – Оу. Егер хz жазықтығын жүргізсек (у=0), онда
=1 болады. Бұл - уz жазықтығында жатқан гиперболаның теңдеуі. Мұның нақты осі – Оу. Егер хz жазықтығын жүргізсек (у=0), онда  -
-  =1. Бұл - хz жазықтығында жатқан гиперболаның теңдеуі. Мұның нақты осі – Ох. Енді хОz жазықтығына параллель у=һ жазықтығын жүргізейік (173-сызба). Осы у-тің мәнін қойып, бір қуысты гиперболоидтың теңдеуін түрлендірейік:
=1. Бұл - хz жазықтығында жатқан гиперболаның теңдеуі. Мұның нақты осі – Ох. Енді хОz жазықтығына параллель у=һ жазықтығын жүргізейік (173-сызба). Осы у-тің мәнін қойып, бір қуысты гиперболоидтың теңдеуін түрлендірейік:
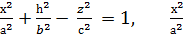 -
-  =1-
=1- 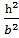 ,
,
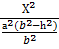 -
-  =1,
=1,
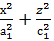 =1,
=1,
мұндағы
а1= 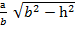 , с1=
, с1= 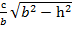 ,
, 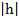 < b.
< b.
Бір қуысты гиперболоидтың қимасындағы гиперболаның нақты жарты осі а1, жорымал жарты осі b1 болады.
 Егер у = һ, (һ)>b болса, онда
Егер у = һ, (һ)>b болса, онда
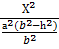 -
- 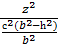 =1,
=1,
немесе
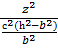 -
- 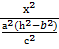 =1,
=1,
с1= 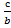
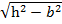 , а1=
, а1= 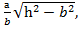
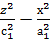 =1.
=1.
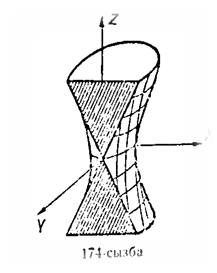
Бұл - хz жазықтықтағы гипербола. Гиперболаның нақты осі -2с1||Оz, жорымал осі – 2а1||Ох. Егер екінші ретті бетті у=b жазықтығымен қисақ (174-сызба), онда екі түзудің теңдеуі шығады:
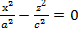 , (
, (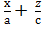 ) (
) (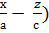 =0,
=0,
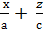 =0,
=0, 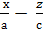 =0.
=0.
Координаталардың бас нүктесінен өтетін бір қуысты гиперболоидтың көлденең қимасы эллипс болады. Оның (О,b,0) төбесінен соңғы екі түзу өтеді. Бір қуысты гиперболоид осы екі түзудің бойымен және у=b жазықтығымен киылысады.
Бір қуысты гиперболоидтың 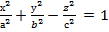 теңдеуін зерттеп мынадай қорытындыға келдік:
теңдеуін зерттеп мынадай қорытындыға келдік:
1) ху жазықтығына параллель z = һ жазықтығын жүргізсек, оның қимасы әрқашанда эллипс болады:
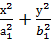 =1, а1=
=1, а1= 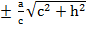 , b1=
, b1= 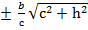 .
.
Бір қуысты гиперболоидты z=0 жазықтығымен қиғанда ең кішкене эллипс шығады: 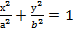 . Ал һ-тің абсолют мәні өскен сайын бір қуысты гиперболоидтың қимасындағы эллипстің мөлшері өседі және ол ху жазықтығына параллель (z =-һ,
. Ал һ-тің абсолют мәні өскен сайын бір қуысты гиперболоидтың қимасындағы эллипстің мөлшері өседі және ол ху жазықтығына параллель (z =-һ,
 z =+һ) жылжып отырады. Бір қуысты гиперболоидтың центрі координаталардың бас нүктесінде жатады. Координаталық осьтер мен координаталық жазықтықтар оның симметриялы осьтері мен симметриялы жазықтықтары болады.
z =+һ) жылжып отырады. Бір қуысты гиперболоидтың центрі координаталардың бас нүктесінде жатады. Координаталық осьтер мен координаталық жазықтықтар оның симметриялы осьтері мен симметриялы жазықтықтары болады.
2) хОz жазықтығына параллель у=һ, һ< b жазықтығын жүргізсек, онда оның қимасы мынадай гиперболалық теңдеумен кескінделеді(173-сызба):
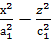 =1, а1=
=1, а1= 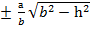 , с1=
, с1=  .
.
3) Егер хОz жазықтығына параллель у=һ, һ>b жазықтығын жүргізсек, онда оның қимасы мынадай теңдеумен кескінделеді (174-сызба):
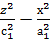 =1, с1=
=1, с1= 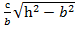 , а1=
, а1= 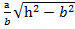 .
.
4) Егер хОz жазықтығына параллель у=b жазықтығын жүргізсек, онда бір қуысты гиперболоид осы жазықтықпен екі түзудің 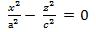 бойымен қиылысады (175-сызба).
бойымен қиылысады (175-сызба).
Сонымен, бір қуысты мына 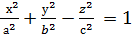 гиперболоидтың қималары мынадай болады:
гиперболоидтың қималары мынадай болады:
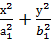 =1 (172-сызба),
=1 (172-сызба),
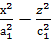 =1 (173-сызба),
=1 (173-сызба),
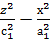 =1 (174-сызба),
=1 (174-сызба),
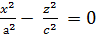 (175- сызба)
(175- сызба)
Енді бір қуысты гиперболоидтың түзу сызықты жасаушыларын қарастырайық. Бір қуысты гиперболоидтың теңдеуін түрлендірейік:
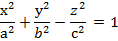
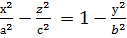 ,
,
(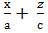 ) (
) (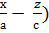 =(1+
=(1+  )(1-
)(1-  ).
).
Осы теңдеуді екі теңдеуге ыдыратып жазуға болады:
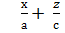 =
= 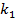 (1+
(1+  )
)
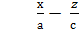 =
= 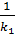 (1-
(1-  ) (І)
) (І)
немесе
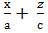 =
= 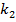 (1-
(1-  )
)
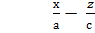 =
= 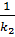 (1+
(1+  ) (ІІ)
) (ІІ)
мұндағы k1 және k2 – кез келген коэффиценттер.
Жеке алғанда төрт теңдеудің әрқайсысы жазықтықты кескіндейді, ал (І),(ІІ) екі теңдеудің жиындысы түзу сызықты кескіндейді. Бірінші (І) және екінші (ІІ) теңдеулердегі х,у,z ағымдық координаталардың мәндері бір қуысты гиперболоидтың теңдеуін де қанағаттандырады. Сондықтан (І),(ІІ) – төрт теңдеулермен анықталатын түзулер бір қуысты гиперболоидтың бетінде жатады. Бұл түзулер бір қуысты гиперболоидтың түзу сызықты жасаушылары деп аталады (176-сызба). k1 және k2 параметрлерінің белгілі мәндерінде (І) және (ІІ) теңдеулер екі түзуді береді. k1 және k2 мәндерін әр түрлі етіп өзгертіп отырсақ, онда осы екі параметрдің мәндеріне сәйкес екі түрлі көп түзулер шығады. Бұл екі түрлі көп түзулерді түзулер үйірімі деп атаймыз. Әрбір нүктенің (х,у,z) координаталары бірінші (І) түзулер үйірімі мен екінші (ІІ) түзулер үйірімінің теңдеулерін қанағаттандырады.Сондықтан бұл түзулер үйірімі түгелдей бір қуысты гиперболоидтың бетінде жатады (176-сызба). Бір қуысты гиперболоидтың әрбір нүктесінен әрбір үйірімнің бір түзуі өтеді.
Теорема. Бір системаға (бір үйірімге) жататын түзу сызықты екі жасаушылар өзара қиылыспайды.Әр түрлі екі системаға (екі үйірімге) жататын кез келген екі түзу сызықты жасаушылар әрқашанда өзара қиылысады, яғни олардың теңдеулерінің жалпы шешімі болады.
Осы теореманы дәлелдейік.
Дәлелдеме. Бір қуысты гиперболоидтың түзу сызықты жасаушылары әр түрлі екі системаға (екі үйірмеге) бөлінсін:
Түзулердің бірінші үйірімі
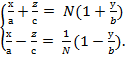 , (ІІІ)
, (ІІІ)
Түзулердің екінші үйірімі
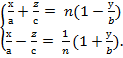 , (
, (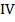 )
)
(ІІІ)-теңдеулердегі N параметрінің әр түрлі мәндеріне N=N1, N=N2 сәйкес шығатын түзулерді бір системаға (бір үйірімге) жататын түзусызықты жасаушылар дейміз, (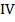 ) теңдеулердегі n параметрлерінің әртүрлі мәндеріне n=n1, n=n2 сәйкес шығатын түзулерді екінші системаға (екінші үйірімге) жататын түзу сызықты жасаушылар дейміз.
) теңдеулердегі n параметрлерінің әртүрлі мәндеріне n=n1, n=n2 сәйкес шығатын түзулерді екінші системаға (екінші үйірімге) жататын түзу сызықты жасаушылар дейміз.
1) Бірінші (ІІІ) системаға жататын түзусызықты жасаушылардың N параметрінің мәндері N=N1, N=N2 болсын. Онда (ІІІ) теңдеулер былайша жазылады (түзулердің бірінші үйірмелері):
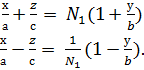 (ІІІ′)
(ІІІ′)
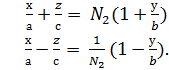 (ІІІ′′)
(ІІІ′′)
Егер осы (ІІІ′),(ІІІ′′) түзулері қиылысса, онда бұл төрт теңдеулердің өзара шешімдері бар. (ІІІ′) түзуінің бірінші теңдеуінен (ІІІ′′) түзуінің бірінші теңдеуін, (ІІІ′) түзуінің екінші теңдеуінен (ІІІ′′) түзуінің екінші теңдеуін мүшелеп алсақ, онда мынау шығады:
(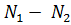 ) (1+
) (1+  ) =0,
) =0,
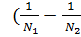 ) (1-
) (1-  ) =0.
) =0.
Осыдан өзара шешілмейтін екі теңдеу шығады:
1 +  = 0, 1 -
= 0, 1 -  = 0
= 0
мұндағы 
Қорыта келгенде, бір системаға жататын кез келген екі түзу сызықты жасаушылар әрқашанда жалпы бір нүктеден қиылыспайды.
2) Енді (ІІІ) теңдеудің біріншісінен (ІV) теңдеудің біріншісін, (ІІІ) теңдеудің екіншісінен (ІV) теңдеудің екіншісін мүшелеп алсақ, онда мынадай болады:
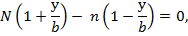
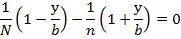
Бұл теңдеудің әрқайсысы у-ті анықтайды. Бұдан шығатын қорытынды: әр түрлі екі системаға жататын кез келген екі түзу сызықты жасаушылар өзара әрқашанда бір нүктеде қиылысады.
(І) және (ІV) теңдеулерден бір қуысты гиперболоидтың х,у,z координаталары N және n параметрлері арқылы өрнектеледі:
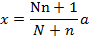
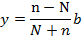
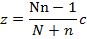
Егер кез келген есептің шартына сәйкес N,n параметрлері анықталса, онда ылғи х,у,z координаталары анықталады.
§30. Екі қуысты гиперболоид
Гиперболаның нақты осінен айналғаннан шығатын екінші ретті бетті екі қуысты гиперболоид деп атайды.Бұл анықтама бойынша мына 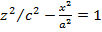 гиперболаны Oz осінен айналдырсақ, онда екі қуысты айналмалы гиперболоидтың формуласы /16/ формула бойынша былай жазылады:
гиперболаны Oz осінен айналдырсақ, онда екі қуысты айналмалы гиперболоидтың формуласы /16/ формула бойынша былай жазылады:

Екі қуысты айналмалы гиперболоидтың теңдеуін мынадай түрде жазайық:


Екінші ретті беттің әрбір нүктесін xOz жазықтығынан мынадай 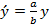 қашықтыққа созсақ,онда M(0.a.0) нүктесі N(0.b.0) нүктесіне көшеді,ал k=a/b k=a/b р қалыпты қысу коэффиценті деп аталады.Екі қуысты айналмалы гиперболоидты айналу осінің бойына қарай екі жағынан бірқалыпты қыссақ,онда екі қуысты гиперболоид шығады. Енді
қашықтыққа созсақ,онда M(0.a.0) нүктесі N(0.b.0) нүктесіне көшеді,ал k=a/b k=a/b р қалыпты қысу коэффиценті деп аталады.Екі қуысты айналмалы гиперболоидты айналу осінің бойына қарай екі жағынан бірқалыпты қыссақ,онда екі қуысты гиперболоид шығады. Енді  мәнін жоғарыда жазылған теңдікке қойып,екі қуысты гиперболоидтың жабайы теңдеуін табамыз:
мәнін жоғарыда жазылған теңдікке қойып,екі қуысты гиперболоидтың жабайы теңдеуін табамыз:
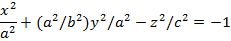
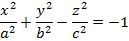
Қима әдісін пайдаланып,екі қуысты гиперболоидтың түрін теңдеуі арқылы зерттейік xOy жазықтығына пареллель z=h жазықтығын жүргізіп, екі қуысты гиперболидтың теңдеуін түрлендірейік:
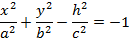
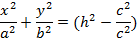
Екі қуысты гиперболоидтың қимасы /1/ эллипс болады. Оның жарты осьтері 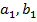 (2) теңдіктерімен кескінделеді.Бұл қиманың қандай болуы h-тың мәніне байланысты: 1) /h/
(2) теңдіктерімен кескінделеді.Бұл қиманың қандай болуы h-тың мәніне байланысты: 1) /h/ 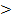 c. 2) h=
c. 2) h= 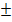 c. 3) /h/
c. 3) /h/  c. Бірінші жағдайда h-тың абсолют мәні c-тен артық болса, екі қуыст ыгиперболоидтың формуласы z=h эллипс болады. Екінші жағдайда эллипстік қима нүктеге айналады, яғни екі қуысты гиперболотдтың екі нүктесі бар:
c. Бірінші жағдайда h-тың абсолют мәні c-тен артық болса, екі қуыст ыгиперболоидтың формуласы z=h эллипс болады. Екінші жағдайда эллипстік қима нүктеге айналады, яғни екі қуысты гиперболотдтың екі нүктесі бар: 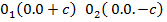 . Бұл нүктелер екі қуысты гиперболоидтың төбелері деп аталады. Үшінші жағдайда екі қуысты гиперболоидтың О1 және О2 төбелерінің арасында, яғни –с пен +с тің арасында қарастырып отырған екінші ретті беттің ешбір нүктесі жоқ.
. Бұл нүктелер екі қуысты гиперболоидтың төбелері деп аталады. Үшінші жағдайда екі қуысты гиперболоидтың О1 және О2 төбелерінің арасында, яғни –с пен +с тің арасында қарастырып отырған екінші ретті беттің ешбір нүктесі жоқ.
Екінші теңдеудегі a1 мен b1 – қима эллипстің жарты осьтері.H-тің абсолют мәні өскен сайын,a1,b1 жарты осьтері де өсіп отырады, яғни қима эллипс үлкейе береді.Сондықтан екі қуысты гиперболоид координаталардың бас нүктесіне симметриялы, төбелері О1 (0.0.-c), O2(0.0.-c) нүктесінен өтетін, қималары z осінің бойымен, осы екі нүктеден жоғары және төмен қарай өсіп отыратын геометриялық бет болады.
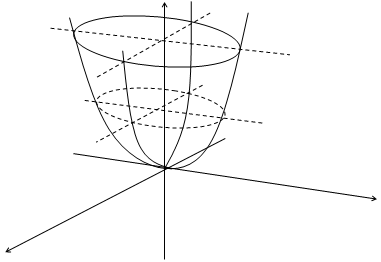 7.Эллипстік параболоид. Бізге
7.Эллипстік параболоид. Бізге 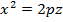 параболасы берілсін.Осы параболаны z сьінен айналдырсақ, бізге белгілі /16/ формула бойынша кеңістік пішін мынадай жаңа теңдеумен кескінделеді:
параболасы берілсін.Осы параболаны z сьінен айналдырсақ, бізге белгілі /16/ формула бойынша кеңістік пішін мынадай жаңа теңдеумен кескінделеді:
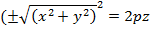
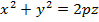
Бұл геометриялық пішінді айналмалы эллипстік параболлоид деп атаймыз,яғни симметриялы осьтен айналдырғаннан шығатын екінші ретті бет айналмалы эллипстік параболоид деп аталады.Айналмалы эллипстік параболоидты y осьінің бағытымен созсақ, онда y=ky1,y’1=y/k болады. Айналмалы эллипстік параболоидтың теңдеуі былайша жазылады:

Енді y’ –тің мәнін осыған қойып, эллипстік параболоидтың жабайы теңдеуін табайық:

Сөйтіп,эллипстік параболоид деп, 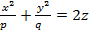 теңдеуімен кескінделетін екінші ретті бетті айтамыз. Енді осы жабайы теңдеуі арқылы эллипстік параболоидтың координаталар системасындағы орналасуын зерттейік.
теңдеуімен кескінделетін екінші ретті бетті айтамыз. Енді осы жабайы теңдеуі арқылы эллипстік параболоидтың координаталар системасындағы орналасуын зерттейік.
Эллипстік параболоидты қиып өтетін xOy жазықтығына параллель z=h жазықтын жүргізейік. Енді /23/ теңдікті мынадай түрде жазайық:
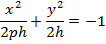
Мұндағы 2ph,2h – тұрақты шамалар. Ендеше эллипстік параболоидтың қимасы эллипс болады. Егер z=h=0 болса, онда 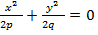 , яғни эллипстік параболоид координаталардың бас нүктесінен өтеді.һйткені бұл теңдеуде x-пен y-тің нольге тең болған мәндерінде қанағаттанады,яғни x=0, y=0, h-тің мәні өскен сайын эллипстік параболоидтың қимасы өсіп отырады, өйткені
, яғни эллипстік параболоид координаталардың бас нүктесінен өтеді.һйткені бұл теңдеуде x-пен y-тің нольге тең болған мәндерінде қанағаттанады,яғни x=0, y=0, h-тің мәні өскен сайын эллипстік параболоидтың қимасы өсіп отырады, өйткені
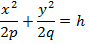
Теңдіктің оң жағы өссе, соған сәйкес сол жағыда өседі, яғни қимасы үлкейеді.
егер z=-h болса, онда 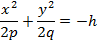
теңдеуінің нақты шешімі жоқ. Ендеше, координаталардың бас нүктесінің төменгі жағында эллипстік параболидтың ешбір нүктесі жоқ, яғни оның барлық нүктелері абсцицца осьінің жоғарғы жағында жатады. Сөйтіп, эллипстік параболоид – координаталардың бас нүктесінен өтіп, z осьіне симметриялы болып, z=+h жоғарылаған сайын өсіп отыратын геометриялық бейне
егер p=q болса 6 онда айналмалы эллипст3к параболоид шы5ады?
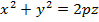
Бұл жағдайда екінші ретті беттің қимасы шеңбер болады
1-мысал. Эллипстік параболоидтың 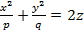 теңдеуі және оның үстінде жатқан бір M (x1,y1,z1) нүктесі берілген. Осы нүктеден эллипстік параболоидқа жанама жазықтық жүргізейік.
теңдеуі және оның үстінде жатқан бір M (x1,y1,z1) нүктесі берілген. Осы нүктеден эллипстік параболоидқа жанама жазықтық жүргізейік.
Ш Е Ш У І: Мына x=x1+lt, y= y1+mt 6 z=z1 + nt параметрлік теңдеулеріндегі М нүктесі эллипстік параболоидтың бойындағы нүкте болсын. Ендеше


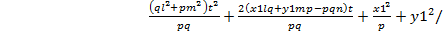 q -2z1=0
q -2z1=0
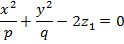
Квадрат теңдеуінің тнбірлері t1=t2 бірдей болу үшін мына шарт орындалу керек:
Енді: 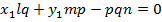

Қатынастарын пайдаланып іздеген теңдеуді табамыз:
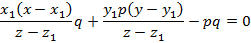
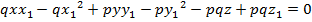

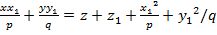 -2z
-2z
Осыдан
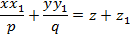
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 3092; Нарушение авторских прав?; Мы поможем в написании вашей работы!