
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Эллипстік параболоид
|
|
|
|
§32. Гиперболоидтық параболоид
Тік бұрышты координаталар системасында 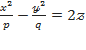 теңдеуімен кескінделетін екінші ретті бетті гиперболалық параболоид деп атаймыз. Мұнда p ˃0, q˃0. Берілген теңдеудегі
теңдеуімен кескінделетін екінші ретті бетті гиперболалық параболоид деп атаймыз. Мұнда p ˃0, q˃0. Берілген теңдеудегі 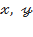 ағымдық координаталары екінші дәрежелі болғандықтан, бұл екінші ретті бет
ағымдық координаталары екінші дәрежелі болғандықтан, бұл екінші ретті бет  жазықтықтарына және
жазықтықтарына және 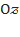 апликата осіне қарағанда симметриялы болады. Екінші ретті беттің
апликата осіне қарағанда симметриялы болады. Екінші ретті беттің  жазықтығымен қиылысатын сызығын анықтау үшін
жазықтығымен қиылысатын сызығын анықтау үшін  нольге тең деп алайық. Енді теңдеу былайша түрленеді:
нольге тең деп алайық. Енді теңдеу былайша түрленеді:
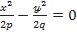 ,
, 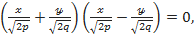
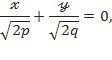
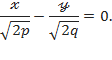
Бұл теңдеулер 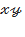 жазықтығындағы екі түзуді кескіндейді. Бұл түзулер координаталардың бас нүктесінен өтеді және
жазықтығындағы екі түзуді кескіндейді. Бұл түзулер координаталардың бас нүктесінен өтеді және 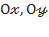 осьтеріне симметриялы болады. Гиперболалық параболоидқа
осьтеріне симметриялы болады. Гиперболалық параболоидқа 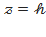 жазықтығын жүргізсек, онда оның
жазықтығын жүргізсек, онда оның  жазықтығындағы параллель қимасы гипербола болады:
жазықтығындағы параллель қимасы гипербола болады:
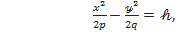
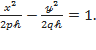
Гиперболаның жарты осьтері 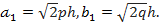 Гипербола төбелерінің арасы
Гипербола төбелерінің арасы  h өскен сайын гипербола осі өсіп отырады. Бұл жағдайда гиперболалық параболоид
h өскен сайын гипербола осі өсіп отырады. Бұл жағдайда гиперболалық параболоид 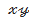 жазықтығының үстінде,
жазықтығының үстінде, 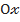 осінің бағытымен шексізге дейін кетеді. H aзайған сайын қима жазықтығы төмендей береді.
осінің бағытымен шексізге дейін кетеді. H aзайған сайын қима жазықтығы төмендей береді. 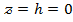 Болғанда қима жазықтығы
Болғанда қима жазықтығы  жазықтығымен беттеседі.
жазықтығымен беттеседі.
Егер екінші ретті бетті 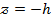 жазықтығымен қисақ, онда оның қимасындағы сызық тағы да гипербола болады:
жазықтығымен қисақ, онда оның қимасындағы сызық тағы да гипербола болады:

Немесе
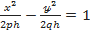
Бұл гиперболадағы нақты жарты ось 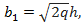 жорымал жарты ось
жорымал жарты ось 
Екінші (II) теңдеу мен үшінші (III) теңдеудің айырмасы, олардың осьтерінің алмасатындығында.
h өскен сайын 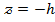 жазықтығы төмендейді.
жазықтығы төмендейді. 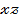 жазықтығы гиперболадық параболоидты
жазықтығы гиперболадық параболоидты  2pz параболаның бойымен қияды,
2pz параболаның бойымен қияды,
яғни егер  болса, онда
болса, онда  2pz болады. Егер
2pz болады. Егер  болса, онда
болса, онда  болады.
болады.
Осы шыққан қорытындыларды пайдаланып гиперболалық параболоидтың графигін салуға болады. 179-сызбада 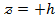 гиперболалық қисықтар, 180,
гиперболалық қисықтар, 180, 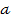 -сызбада гиперболалық параболоидқа жүргізілген жазықтықтың қималары, ал 180, б-сызбада гиперболалық параболоидтың сыртқы пішіні көрсетілген. 179-сызбадағы қималар: гиперболалар -
-сызбада гиперболалық параболоидқа жүргізілген жазықтықтың қималары, ал 180, б-сызбада гиперболалық параболоидтың сыртқы пішіні көрсетілген. 179-сызбадағы қималар: гиперболалар -  ; параболалар -
; параболалар - 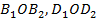 .
.
§33.Гиперболалық параболоидтың түзу сызықты жасаушылары.
Гиперболалық параболоидтың түзу сызықты жасаушыларының теңдеулерін шығару үшін, гиперболалық параболоидтың теңдеуін түрлендірейік:
 (25)
(25)
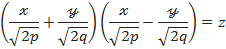
Осыдан екі теңдеулер системасын құрайық:
 (I)
(I)
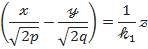
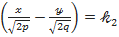 (II)
(II)

Мұндағы 
 - еркінше алынған сандар – параметрлер.
- еркінше алынған сандар – параметрлер.
Осы теңдеулердің әрқайсысы жазықтықты кескіндейді, екі (I), (II) теңдеудің жиындылары екі түзуді береді. Бұл түзулер гиперболалық параболоидтың түзу сызықты жасаушылары деп аталады (181 және 182-сызбалар). Осы (I), (II) теңдеулеріндегі x, y, z ағымдық координаталардың мәндері гиперболалық параболоидтың теңдеуін қанағаттандырады. Сондықтан түзу сызықты жасаушылар гиперболалық параболоидтың бетіне жатады. Бір қуысты гиперболоид сияқты гиперболалық параболоидтың әрбір нүктесінен екі түзу сызықты жасаушылар өтеді, оның біреуі әрқашанда бірінші системадан болса, ал екіншісі әрқашанда екінші системадан болады (181 және 182-сызбалар). Бір системаның түзулері өз ара қиылыспайды. Сөйтіп, мұнда екі түрлі түзулер үйірімі болады. Бұл түзулердің біреуі бірінші системамен (I), екіншісі екінші (II) системамен кескінделеді. 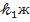 әне
әне  параметрлерінің мәндеріне байланысты түзулер үйірімінің осыларға сәйкес теңдеулері шығады. Берілген есептің шарты бойынша және параметрлердің мәндерін табуға болады. Табылған теңдеулері арқылы гиперболалық параболоидтың түзу сызықты жасаушыларының тік бұрышты координаталар системасында қандай болып өтетінін қарастыру қиын емес.
параметрлерінің мәндеріне байланысты түзулер үйірімінің осыларға сәйкес теңдеулері шығады. Берілген есептің шарты бойынша және параметрлердің мәндерін табуға болады. Табылған теңдеулері арқылы гиперболалық параболоидтың түзу сызықты жасаушыларының тік бұрышты координаталар системасында қандай болып өтетінін қарастыру қиын емес.
§34. Екінші ретті беттің дөңгелектік қималары
Егер екінші ретті жазықтық жүргізгенде оның қимасы шеңбер болса,онда мұндай қиманы екінші ретті бетттің дөңгелектік қимасы дейміз.Екінші ретті беттің нүктелерінде жанама жазықтықтар дөңгелектік қималарға параллель болса,онда мұндай нүктелерді дөңгелену нүктелері дейміз. Ең алдымен екінші ретті беттің дөңгелектік қималарынынң теңдеулерін қорытып шығарайық. Сонан кейін дөңгелену нүктелерінің координаталарын табатын формулаларды келтірейік.
1)Әуелі эллипсоидтың теңдеуін алайық:
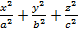 -1=0.
-1=0.
Енді координаталардың бас нүктесінен өтетін шардың

Теңдеуін эллипсоидтың теңдеуінен алсақ,онда мынадай теңдеу шығады.
 (26)
(26)
Бұл теңдеу эллипсоид пен шардың қиылысатын сызығынан өтетін екінші ретті бетті сипаттайды. Дәлірек айтқанда,бұл теңдеу төбесі координаталардың бас нүктесінде болатын конустық бетті сипаттайды.Егер (26) теңдеудің коэффициенттерінің біреуі нольге тең болса,онда ол екі жазықтықтың теңдеулерін береді. Мысалы,  болғанда,мына коэффициент ноль болсын:
болғанда,мына коэффициент ноль болсын:
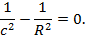
Сонда (26) теңдеуден мынадай теңдеулерді табамыз:
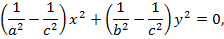
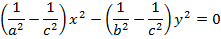
немесе
 (27)
(27)
Қойылған шарт бойынша  . Сондықтан эллипсоидтың бұл қималары жорымал болады.
. Сондықтан эллипсоидтың бұл қималары жорымал болады.
Енді 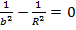 болса,онда (26) теңдеуді жоғарғыдай түрлендіріп, мынаны табамыз:
болса,онда (26) теңдеуді жоғарғыдай түрлендіріп, мынаны табамыз:
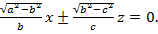 (28)
(28)
Мұндағы  болғандықтан, (28) қималар нақты болады. Бұл жазықтықтар екінші ретті бетті шеңбердің бойымен қияды.
болғандықтан, (28) қималар нақты болады. Бұл жазықтықтар екінші ретті бетті шеңбердің бойымен қияды.
Сонымен, (26) теңдеуден жазықтықтардың дөңгелектік қималарының үш түрлі теңдеулері шығады:
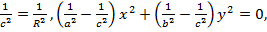 (27)
(27)
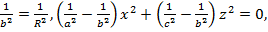 (28)
(28)
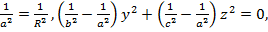 (29)
(29)
Осылардың әрқайссыс дөңгелектік екі қима жазықтықтарды береді. Ал  болғандықтан, дөңгелектік нақты жазықтықтар (28) теңдеулермен сипатталады, яғни (28) теңдеу нақты қималарды көрсетеді,қалған (27 және 29) теңдеулер жорымал қималарды береді. Сөйтіп (28) теңдеулер мына екі теңдеуден құрылған:
болғандықтан, дөңгелектік нақты жазықтықтар (28) теңдеулермен сипатталады, яғни (28) теңдеу нақты қималарды көрсетеді,қалған (27 және 29) теңдеулер жорымал қималарды береді. Сөйтіп (28) теңдеулер мына екі теңдеуден құрылған:
 (28`)
(28`)
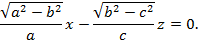
Енді (28) теңдеулерінің екі жазықтығына паралллель жазықтықтар былайша жазылады:
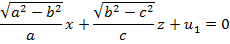
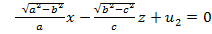 (30)
(30)
Бұл (30) жазықтықтар – эллипсоидтың центрінен өтетін (28`) жазықтықтарына параллель болатын жазықтықтар. Мұндағы 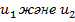 кез келген параметрлерді көрсетеді.
кез келген параметрлерді көрсетеді.
Сонымен, қорыта келгенде эллипсоидтың центрінен өтетін дөңгелектік жазықтықтарға параллель болатын кез келген жазықтықтар эллипсоидтың дөңгелектік қималары болады.
Бір қуысты гиперболоидтың дөңгелектік қималарының теңдеулері де осы әдіспен шығады. Оның дөңгелектік қималарының нақты жазықтықтары мынадай болады:

немесе
 (30`)
(30`)
Бір қуысты гиперболаның бұдан басқа дөңгелектік қималары жорымал болады.
Екі қуысты гиперболоидтың дөңгелектік қималарының нақты жазықтықтарының теңдеулері:
 (30`)
(30`)
(30`) жазықтықтарына параллель қима жазықтықтар мынадай болады:
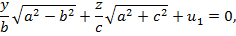
 (30``)
(30``)
мұндағы 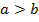 . Енді
. Енді

эллипстік параболоидты алайық. Мұның төбесінен өтетін бір
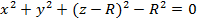
Шарды алып,оның теңдеуіне сәйкес эллипстік параболоидтың теңдеун алсақ,онда мынадай теңдеу шығады:
 (31)
(31)
Шардың теңдеуін былайша жазуға болады:
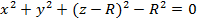
немесе
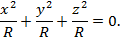
(31) теңдеуі шар мен параболоидтың қиылысатын сызығынан өтетін және төбесі координаталардың басында жатқан конустық бетті сипаттайды.(31) теңдеудің сол жағындағы коэффициенттер 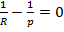 ,
, 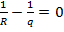 болса,онда конус екі жазықтыққа айналады. Егер
болса,онда конус екі жазықтыққа айналады. Егер 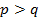 және
және 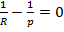 болса,онда дөңгелектік қималардың теңдеуі мынадай болады:
болса,онда дөңгелектік қималардың теңдеуі мынадай болады:
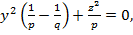 (31`)
(31`)
мұндағы  ,
, 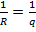 .
.
(31`) теңдеуі –екі дөңгелектік жазықтың теңдеулері. Олар мынадай түрде жіктеледі:
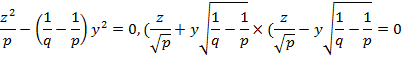
немесе
 (31``)
(31``)
Осы жазықтықтарға параллель жазықтықтар эллипстік параболоидты шеңбердің бойымен қияды,яғни бұл теңдеулер параболоидтың дөңгелектік екі қимасын сипаттайды.Соңғы (31``) теңдеуді 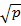 -ға қысқартып,жекелеп жазсақ,мынадай болады:
-ға қысқартып,жекелеп жазсақ,мынадай болады:
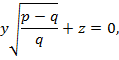
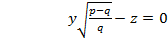 (31```)
(31```)
Енді осы жазықтықтарға параллель дөңнгелектік жазықтықтарға теңдеулерді былайша жазылады:
 (31````)
(31````)

Мұндағы 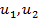 - параметрлер.
- параметрлер.
(31````) теңдеулері эллипстік параболоидтың дөңгелектік (қимасындағы) кез келген параллель жазықтықтарын сипаттайды.
2) Дөңгелену нүктелерінің координаталарын анықтайтын формулаларды шығарайық. Эллипсоидтың жанасу нүктесінің координаталары 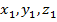 болсын. Онда
болсын. Онда

жанама жазықтығы (28`) теңдеудің екі жазықтығына параллель болғандықтан, мына
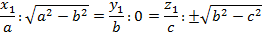
шарттар орындалады, яғни бұл – екі жазықтықтың параллельдік шарттары. Енді эллипсоидтың теңдеуі мен бұл теңдеулерді біріктіріп шығарайық:
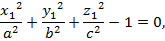
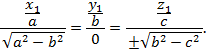
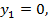 сонда
сонда

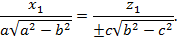
Соңғы теңдеулер системасынан:
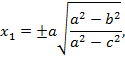
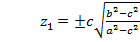 (32)
(32)

Сөйтіп, эллипсоидтың дөңгелену нүктелерінің координаталары осы формулалармен анықталады.Екі қуысты гиперболоидтың дөңгелену нүктелерінің координаталарын осы әдіспен табамыз.
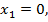
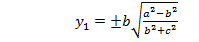 (32`)
(32`)
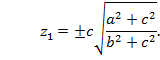
Бір қуысты гиперболоидтың нақты дөңгелену координаталары тіпті жоқ. Эллипстік параболоидтың дөңгелену координаталары жоғарғы айтылған әдіспен табылады:
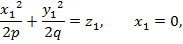
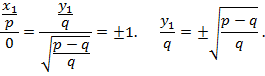
Сөйтіп,дөңгелектену нүктелерінің координаталары былай анықталады:
 ,
,
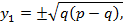
 (32``)
(32``)
мұндағы 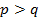 ; p және q параметрлерінің сандық мәндері берілсе,дөңгелену координаталары осы (32``) формуласымен табылады.
; p және q параметрлерінің сандық мәндері берілсе,дөңгелену координаталары осы (32``) формуласымен табылады.
§35.Айнымалы беттер және олардың теңдеулері
Айнымалы беттерге тағы бір рет тоқталып,оған әр түрлі мысалдар келтірейік. Егер жазықтықтағы бір сызықтың F(x,y)=0 теңдеуі берілсе, онда осы сызықты абцисса осінен айналдырғаннан шыққан геомет-риялық дене екінші ретті бет болады. Бұл айналмалы екінші ретті беттің теңдеуі жалпы түрде мынадай болады (4-параграфты қараңдар):
F(x 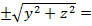 0.
0. 
Жазықтықтағы түзу сызықты немесе қисық сызықты бір осьтен айналдырғанда бұл формула бойынша әрқашанда бір кеңістік дене шығады.
Берілген есептің шартын толық пайдаланып,жоғарғы айтылған формула бойынша айналмалы дененің теңдеуін дұрыс құрып, оның координаталар системасында қалай салынатынын айқын білу керек. Сондықтан осы мәселені қарастыру үшін бірнеше мысалдар келтірейік.
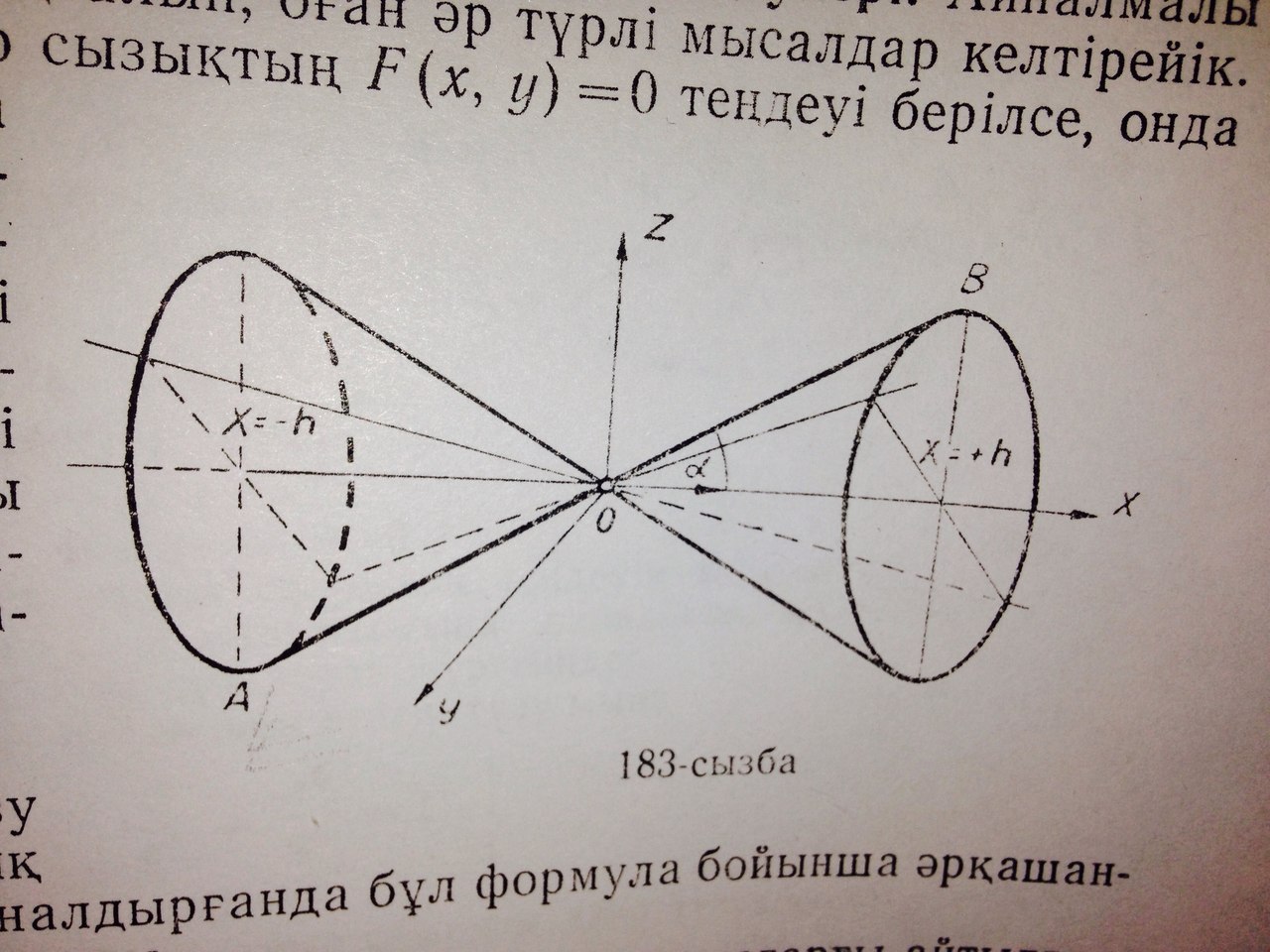
1-мысал. Координаталардың бас нүктесінен өтетін y=kx түзуі берілсін.Осы түзуді Ох осінен айналдырсақ, оның геометриялық орындары конус болады. Бұл конустың теңдеуі:

немесе 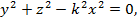
мұндағы k=tgα,α- конустың жасаушысы мен айналдыратын осьтің арасындағы бұрыш (183-сызба).
183-сызбадағы  -қиюшы жазықтар.Олар уОz жазықтығына параллель. Бұл конустың теңдеуі
-қиюшы жазықтар.Олар уОz жазықтығына параллель. Бұл конустың теңдеуі 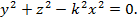 Ол Ох осіне және координаталырдың бас нүктесіне симметриялы болады. АВ түзуін абцисса осінен айналдырдық (183-сызба).
Ол Ох осіне және координаталырдың бас нүктесіне симметриялы болады. АВ түзуін абцисса осінен айналдырдық (183-сызба).
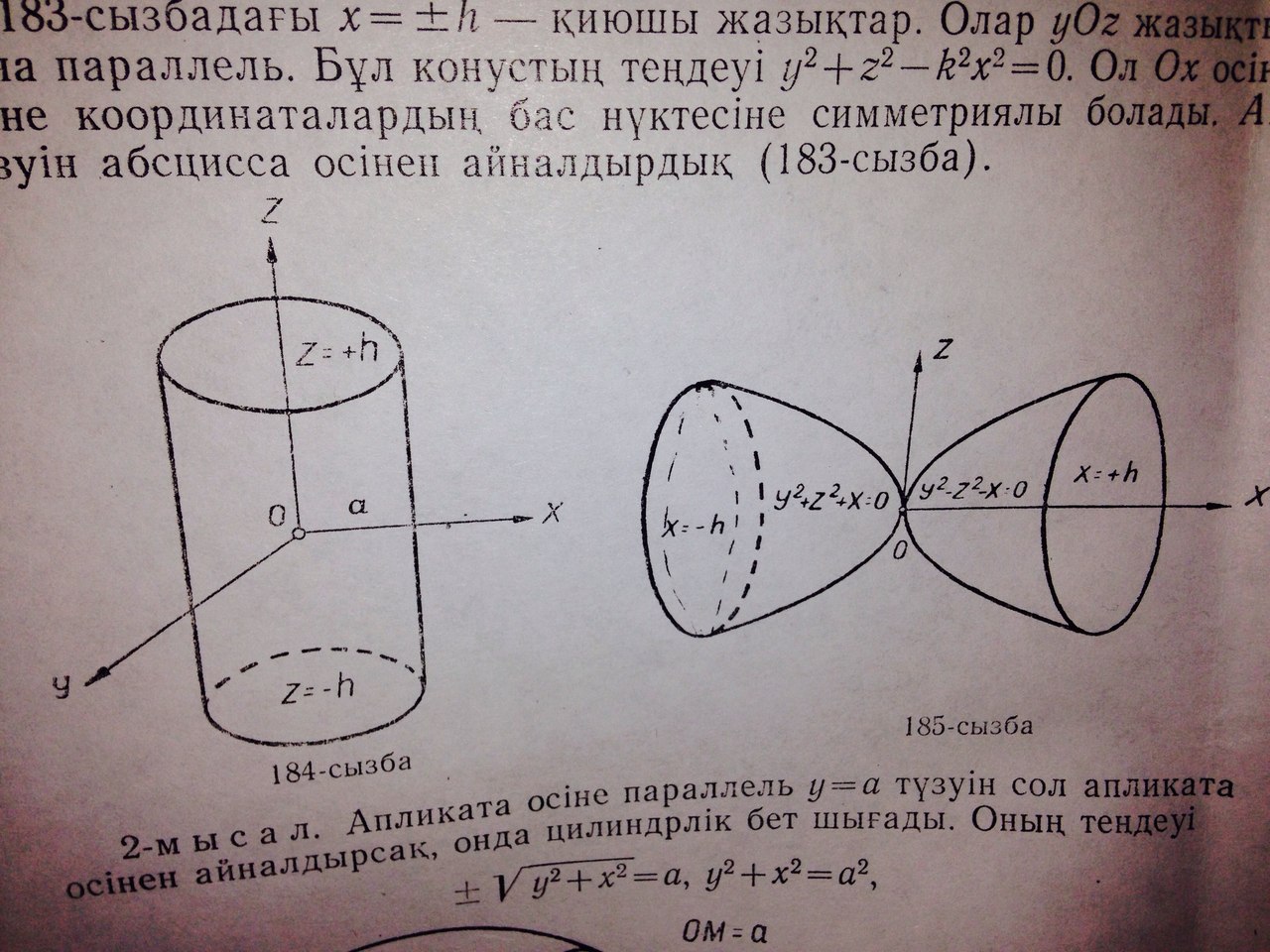
2-мысал. Апликата осіне параллель 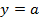 түзуін сол апликата осінен айналдырсақ,онда цилиндрлік бет шығады. Оның теңдеуі
түзуін сол апликата осінен айналдырсақ,онда цилиндрлік бет шығады. Оның теңдеуі
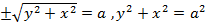 ,
,

мұндағы а-цилиндрдің дөңгелек қимасының радиусы (184-сызба).
3-мысал. Мына  параболаны Ох осінен айналдырсақ,онда айналмалы параболоид шығады (185-сызба). Оның теңдеуі:
параболаны Ох осінен айналдырсақ,онда айналмалы параболоид шығады (185-сызба). Оның теңдеуі:

Егер 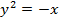 болса, онда
болса, онда  айналмалы параболоид шығады (185-сызбаға қараңдар).
айналмалы параболоид шығады (185-сызбаға қараңдар).
4-мысал. Центрі (а,0), радиусы 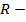 ге тең
ге тең  шеңберін Оy осінен айналдырғаннан шығатын геометриялық денені тор деп атайды (186-сызба). Оның теңдеуі
шеңберін Оy осінен айналдырғаннан шығатын геометриялық денені тор деп атайды (186-сызба). Оның теңдеуі

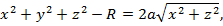
мұндағы R 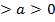 . Тор сақина тәрізді дене (187-сызба). Бұл тордың әрбір қимасы дөңгелек болады (186-сызбада төрт қимасы көрсетілген).
. Тор сақина тәрізді дене (187-сызба). Бұл тордың әрбір қимасы дөңгелек болады (186-сызбада төрт қимасы көрсетілген).
5-мысал. Мынадай 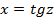 теңдеуімен берілетін сызықтық Oz осінен айналғаннан шығатын кеңістік дененің теңдеуі:
теңдеуімен берілетін сызықтық Oz осінен айналғаннан шығатын кеңістік дененің теңдеуі:

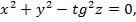
мұнда 0=z 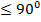 (188-сызба).
(188-сызба).
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 2716; Нарушение авторских прав?; Мы поможем в написании вашей работы!